【图的遍历】广度优先遍历（DFS）、深度优先遍历（BFS）及其应用

无向图满足约束条件的路径

•【目的】：掌握深度优先遍历算法在求解图路径搜索问题的应用

【内容】：编写一个程序，设计相关算法，从无向图G中找出满足如下条件的所有路径：
  （1）给定起点u和终点v。
  （2）给定一组必经点，即输出的路径必须包含这些点。
  （3）给定一组必避点，即输出的路径必须不能包含这些点。

【来源】：《数据结构教程（第五版）》李春葆著，图实验11。

代码：

 #include<stdio.h>
 #include<malloc.h>
 #define MAXV 20
 typedef struct ANode
 {
     int adjvex;
     struct ANode *nextarc;
 } ArcNode;

 typedef struct
 {
     ArcNode *adjlist[MAXV];
     int n1, e1;
 } AdjGraph;

 int visited[MAXV];
 int v1[MAXV], v2[MAXV], n, m;  // v1为必过点集合， v2为必避点集合；n为必过点的个数， m为必避点个数
 int count = ; //路径个数

 void CreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n1, int e1)
 {
     int i, j;
     ArcNode *p;
     G = (AdjGraph*)malloc(sizeof(AdjGraph));
     for (i = ; i < n1; ++i)
         G->adjlist[i] = NULL;
     for (i = ; i < n1; ++i)
         for (j = n1; j >= ; --j)
             if (A[i][j] == )
         {
             p = (ArcNode*)malloc(sizeof(ArcNode));
             p->adjvex = j;
             p->nextarc = G->adjlist[i];
             G->adjlist[i] = p;
         }
     G->n1 = n1;
     G->e1 = e1;
 }

 bool comp(int path[MAXV], int d)
 {
     int flag1 = , f1, flag2 = , f2, j;
     for (int i = ; i < n; ++i)
     {
         f1 = ;
         for (j = ; j <= d; ++j)
             if (path[j] == v1[i])
             {
                 f1 = ;
                 break;
             }
         flag1 += f1;
     }   

     for (int i = ; i < m; ++i)
     {
         f2 = ;
         for (j = ; j <= d; ++j)
             if (path[j] == v2[i])
             {
                 f2 = ;
                 break;
             }
         flag2 += f2;
     }    

     if (flag1 ==  && flag2 == )
         return true;
     else
         return false;
 }

 void findpath(AdjGraph *G, int u, int v, int d, int path[MAXV])
 {
     int i;
     ArcNode *p;
     visited[u] = ;
     ++d; path[d] = u;
     if (u == v && comp(path, d))
     {
         printf("路径%d：", ++count);
         printf("%d", path[]);
         for (i = ; i <= d; ++i)
             printf("->%d ", path[i]);
         printf("\n");
     }
     p = G->adjlist[u];
     while (p != NULL)
     {
         if (visited[p->adjvex] == )
             findpath(G, p->adjvex, v, d, path);
             p = p->nextarc;
     }
     visited[u] = ;
 }

 int main()
 {
     AdjGraph *G;
     int u, v; // u为起点，v为终点
     int path[MAXV];
     int A[MAXV][MAXV] = {
     {, , , , , , , , , , , , , , },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  },
     {, , , , , , , , , , , , , ,  } };
     CreateAdj(G, A, , );
     printf("输入起点和终点：");
     scanf("%d %d", &u, &v);
     printf("输入必过点个数: ");
     scanf("%d", &n);
     printf("输入必过点集合：");
     for (int i = ; i < n; ++i)
         scanf("%d", &v1[i]);
     printf("输入必避点个数: ");
     scanf("%d", &m);
     printf("输入必过点集合：");
     for (int i = ; i < m; ++i)
         scanf("%d", &v2[i]);
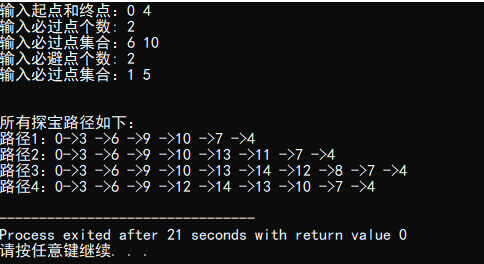
         printf("\n\n所有探宝路径如下：\n");
     findpath(G, u, v, -, path);
     return ;
 }

运行结果：

用图搜索方法求解迷宫问题

•【目的】：深入掌握图遍历算法在求解实际问题中的运用

【内容】：编写一个程序，完成如下功能：
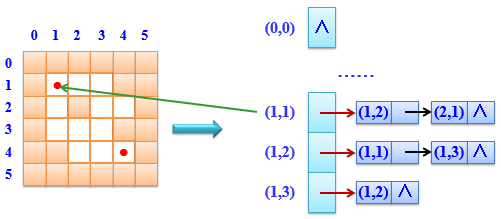
  （1）  建立迷宫对应的邻接表
  （2）  采用深度优先遍历算法输出从入口(1, 1)到出口（M，N）的所有迷宫路径

【来源】：《数据结构教程（第五版）》李春葆著，图实验14。

代码：

 #include<stdio.h>
 #include<malloc.h>
 #define MAXV  20
 #define N 4
 #define M 4
 typedef struct ANode
 {
     int i, j;      // i为横坐标， j为纵坐标
     struct ANode *nextarc;
 } ArcNode;

 typedef struct
 {
     ArcNode *mg[N + ][M + ];
 } AdjGraph;

 typedef struct
 {
     int i;
     int j;
 } Box;

 typedef struct
 {
     Box data[MAXV];
     int length;
 } Path;

 int visited[N + ][M + ] = {  };

 void CreateAdj(AdjGraph *&G, int A[N + ][M + ], int n, int m)
 {
     int i, j, k, i1, j1;
     ArcNode *p;
     G = (AdjGraph *)malloc(sizeof(AdjGraph));
     for (i = ; i < n + ; ++i)
         for (j = ; j < m + ; ++j)
             G->mg[i][j] = NULL;
     for (i = ; i <= n; ++i)
         for (j = ; j <= m; ++j)
             if (A[i][j] == )
             {
                 k = ;
                 while (k <= )
                 {
                     switch (k)
                     {
                     case : i1 = i - ; j1 = j; break;
                     case : i1 = i; j1 = j + ; break;
                     case : i1 = i + ; j1 = j; break;
                     case : i1 = i; j = j - ; break;
                     }
                     ++k;
                     if (A[i1][j1] == )
                     {
                         p = (ArcNode*)malloc(sizeof(ArcNode));
                         p->i = i1;
                         p->j = j1;
                         p->nextarc = G->mg[i][j];
                         G->mg[i][j] = p;
                     }
                 }
             }
 }

 void findpath(AdjGraph *G, int x1, int y1, int xe, int ye, Path pa)
 {
     ArcNode *p;
     ++pa.length;
     pa.data[pa.length].i = x1;
     pa.data[pa.length].j = y1;
     visited[x1][y1] = ;
     if (xe == x1 && ye == y1)
     {
         for (int u = ; u <= pa.length; ++u)
             printf(" (%d, %d) ", pa.data[u].i, pa.data[u].j);
     }

     p = G->mg[x1][y1];
     while (p != NULL)
     {

         if (visited[p->i][p->j] == )
             findpath(G, p->i, p->j, N, M, pa);
         p = p->nextarc;
     }
     visited[x1][y1] = ;
 }

 int main()
 {
     AdjGraph *G;
     Path pa;
     int A[N + ][M + ] = {
         { , , , , ,  },{ , , , , ,  },
     { , , , , ,  },{ , , , , ,  },
     { , , , , ,  },{ , , , , ,  } };
     CreateAdj(G, A, N, M);
     pa.length = -;
     findpath(G, , , N, M, pa);
     return ;
 }

求解两个动物之间通信最少翻译问题

•【目的】：掌握广度优先遍历算法在求解实际问题中的运用

【内容】：编写一个程序，完成如下功能：
据美国动物分类学家欧内斯特-迈尔推算，世界上有超过100万种动物，各种动物有自己的语言。假设动物A只能与动物B通信，所以，动物A、C之间通信需要动物B来当翻译。问两个动物之间项目通信至少需要多少个翻译。
     测试文本文件test.txt中第一行包含两个整数n（2<= n <= 200）、m（1 <= m <= 300），其中n代表动物的数量，动物编号从0开始，n个动物编号为0 ~ n-1，m表示可以相互通信动物数，接下来的m行中包含两个数字分别代表两种动物可以相互通信，在接下来包含一个整数k（k <= 20）,代表查询的数量，每个查询，输出这两个动物彼此同喜至少需要多少个翻译，若它们之间无法通过翻译来通信，输出-1.

输入样本      输出结果

                  1             

【来源】：《数据结构教程（第五版）》李春葆著，图实验12。