欧拉函数小结 hdu2588+

从费马小定理到欧拉定理 欧拉公式 再到欧拉函数。，。 小结一下欧拉函数吧

对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）----定义

欧拉函数的基本公式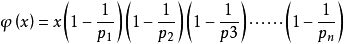其中pi为x的素因子 。公式的推导根据欧拉公式（积性函数的性质）+算术基本定理+phi(p^k)=p^k-p^（k-1）（p为素数）

简单应用

1.hdu 2588

题意：给定N,M求gcd(i,N)>=M的i的个数（1<=i<=N,M<=N)

题解 :  对于每个i因为i<=N 所以g=gcd(N,i)一定是N的因子 ，那么我们可以枚举N的所有因子g，设theta（g）为每个因子g对应的解的集合，那么theta(g1)+theta(g2)+...theta(gn)就是我们要的最终结果。（喵的网上看了一堆评论 说的都不怎么合理，自己整理一下）对于每一个因子g，最小的满足g=gcd(i,n)的i就为g（因为g一定为n的因子）,这里要求的是gcd(i,n)>=M的情况，那么gcd(i*x,n）（1<=x<=(n/i)）的情况也是满足的，为了避免和其他因子枚举出的结果产生重复的结果，也就是i*x不能等于q*z,q为n的其他因子。i*x能够变成其他因子枚举结果的条件是x与(n/i)不互质（两个数不互质，说明他们有相同的数根，这里i如果乘上一个与（n/i）不互质的数，那么就会成为n的其他因子（用反证法证明：这里我们把n划为i、n/i两个部分，i乘上一个与n/i不互质的数字p=k*t,k为gcd(n/i,p),那么i*p=i*k*t,这里i*k一定为n的因子））

由于数据很大 ，我们在枚举的时候有一个小技巧，具体看代码。

ac代码：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
int euler(int key)// 对比较大的数 用这个方法求比较有效
{
    if(key==) return ;
    int temp=key;
    for(int i=; i*i<=key ;i++)// 利用算术基本定理
    {
        if(key%i==)
        {
            temp=temp/i*(i-);
            while(key%i==) key/=i;// 关键步骤 很有意思
        }
    }
    if(key > ) temp=temp/key*(key-);//
    return temp;
}
/*
int eu[10000];
int geteuler()// 对数据小的情况 用筛法可以有效求出多个数的euler
{
    for(int i=1;i<=10000;i++) eu[i]=i;
    for(int i=2;i<=10000;i++)
    {
        if(eu[i]==i)
        {
            for(int j=i;j<=10000;j++)
            {
                eu[j]=eu[j]/i*(i-1);
            }
        }
    }
}
*/
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,m;
        cin>>n>>m;
        int sum=;
        for(int i=;i*i<=n;i++)// 因子总是成对出现的 我们枚举的时候 只用枚举一边就可以了
        {
            if(n%i==)// 是约数
            {
                int key=n/i;
                if( i>=m ) sum+=euler(key);
                if( key>=m && i*i!=n) sum+=euler(i);// 避免i*i的情况计算两次
            }
        }
        cout<<sum<<endl;
    }
    return ;
}

2.hdu 3501

题意：求小于n且不与n互素的数之和

题解：有一个知识点。 当i<=n  if gcd(n,i)=1 then gcd(n,n-i)=1;

我们用  反证法来看  这个 假设gcd（n,i）=1 gcd(n,n-i)=k (k!=1) 那么就有 n%k==0 (n-i)%k==0-> n=i(mod k) 这个结论与前面gcd(n,i)=1矛盾 所以 if gcd(n,i) then gcd(n,n-i)=1。有这个结论就好解决这道题目了。我们求小于n且不于n互素的数之和，只要用小于n的数之和减去与n互素的数之和。由于和n互素的数字都是成对出现的，且和为n。

ac代码：

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
const ll mod=;
ll euler(ll n)
{
    ll temp=n;
    for(ll i=;i*i<=n;i++)
    {
        if(n%i==)
        {
            temp=temp/i*(i-);
            while(n%i==) n/=i;
        }
    }
    if(n>) temp=temp/n*(n-);
    return temp;
}
int main()
{
    ll n;
    while(cin>>n&&n)
    {
        if(n==)
        {
            cout<<<<endl;
            continue;
        }
        ll temp=n*(n+)/-n;
        ll zz;
        zz=euler(n)/*n;
        zz=(temp-zz)%mod;
        if(zz<) zz+=mod;
        cout<<zz<<endl;
    }
    return ;
}

一步一个脚印才是实实在在的进步。共勉。。。