DP&图论 DAY 4 下午图论

DP&图论  DAY 4  下午

后天考试不考二分图，双联通

考拓扑排序

图论

图的基本模型

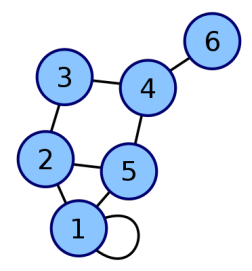
边：

有向边构成有向图

无向边构成无向图

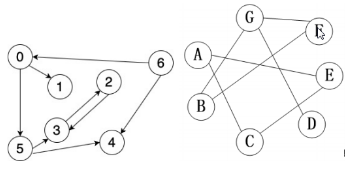
权值：

1.无权

2.点权

3.边权

4.负权（dij不可以跑）

环：

1.

2.重边

3.有向无环图DAG

路径：

1.简单路径：不经过重复的点  1-->2-->3

不简单路径：经过重复点  1-->2-->3-->1-->4

2.连通，具有传递性

图：

1.树：n个点，n-1条边的无环连通图

2.完全图：一个无向图，图中任意两点之间都有一条连边

3.竞赛图：完全图中的每一条边确定一个方向

4.基环树

5.仙人掌：不是树，图里可以成环，每一条边，要么不在环上，要么只属于一个环

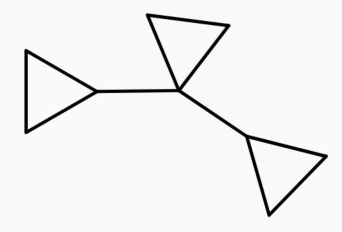
图的输入方式

图的存储方式

图的遍历方法

拓扑排序基于BFS

三种遍历顺序

1.前序遍历   中左右

2.中序遍历   左中右

3.后序遍历   左右中

QUS：给前序中序，写后序

前序第一个就是根，找到在中序的位置，递归

例题1：

给定一个有向图，边权为 1 或 2，求单源最短路。

>Solution

稍微改写一下 BFS 即可。
# 创建三个集合， Q0 表示当前层， Q1 表示距离为 1 的层，
Q2 表示距离为 2 的层，初始 Q0 = {s}, Q1= ∅, Q2= ∅
# 依次取出 Q0 中的点，将其邻点放入对应的 Q1 或 Q2 中
# Q0 = Q1, Q1 = Q2, Q2 = ∅
注意一个点可能和当前层既有长度为 1 的边，又有长度为 2 的
边，应当将其加入 Q1 而非 Q2。

bfs：

建立一个辅助点

每个权是2的边u→v  ，都改成   u→辅助点，辅助点→v  ，权为1 ，这样边权就都是1

bfs就行了

例题2

给出一个有向图和起点 s，对每条边 < u, v > 回答，如果删去这
条边，从 s 到 v 的最短路长度是否会改变。

>Solution

# BFS 求出从 s 出发的单源最短路
# 建立最短路图，即保留满足 dv = du + 1 的边 < u, v >

#如果询问的边不在最短路图中，那么删掉不改变
# 在最短路图上，如果 v 的入度为 1，则该入边是从 s 到 v
的必经边，若删去则 v 的最短路长度会改变
# 在最短路图上，如果 v 的入度大于 1，则删去任何一条入
边， v 的最短路长度都不会改变

拓扑排序

有向无环图的拓扑排序即将所有顶点排为线性序列，使得对于任意的 < u, v >∈ E，都有 u 在线性序列中出现于 v 之前。
有向图中如果有环，则一定不存在拓扑排序；如果没有环，则一定存在拓扑排序。

# 选取一个入度为 0 的点记为 u
# 将 u 添加到线性序列末端
# 删去所有 u 的出边
# 重复上述步骤直到所有点都被加入序列

void topsort()
{
    queue<int> q;
    for(int i=;i<=n;i++)
      if(!in[i])
        q.push(i);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        ans[++cnt]=u;
        for(int i=head[u];i;i=edge[i].nxt)
        {
            int y=edge[i].v;
            in[y]--;
            if(!in[y]) q.push(y);
        }
    }
    if(cnt!=n) printf("you fu huan!!!");
}

// Tuo Pu Pai Xu
void toposort() {
    static int que[mxn];
    int l = , r = ;
    for (int i = ; i <= n; ++i)
        if (cnt[i] == )
            que[r++] = i;
    while (l != r) {
        int u = que[l++];
        for (int i = hd[u], v; i; i = nt[i])
            if (--cnt[v = to[i]] == )
                que[r++] = v;
    }
}

YouSiki's Code

例题1

有 n 项任务，有 m 个限制，第 i 个限制要求执行任务 ui 之前
必须要完成任务 vi。请问是否存在合适的任务执行顺序，满足所
有的限制。

>Solution

将每个任务视为一个点，任务之间的依赖构成了有向边。如果该
有向图中没有环，则存在拓扑排序，而拓扑排序就是可行的任务
执行顺序；如果该有向图中存在环，则无解。

例 2
有 n 项任务，有 m 个限制，限制有如下两种：
   # 执行 u 任务之前必须要完成 v 任务
   # 存在某一时刻， u 和 v 任务都在执行
请问是否存在安排每个任务起始时间和结束时间的方案，满足所
有的限制。

>Solution

为每个任务的起始时间和结束时间各对应一个点，任务 i 的起始
时间点记为 s_i，结束时间点记为 e_i。
# 要保证每个任务的结束时间在起始时间之后，所以对所有 i，连边 < s_i, e_i >
# 如果要求任务 a 在任务 b 开始执行之前完成，则连边< e_a, s_b >
# 如果要求任务 a 和 b 在某个时刻都在执行，则连边< s_a, e_b >, < s_b, e_a >
对于上面的有向图，如果存在环则无解，否则根据其拓扑排序易构造一个方案。

例 3
对于带边权的有向无环图，求单源最短路。
>Solution

POJ 1094 Sorting It All Out
An ascending sorted sequence of distinct values is one in which
some form of a less-than operator is used to order the elements
from smallest to largest. For example, the sorted sequence A, B,
C, D implies that A < B, B < C and C < D. in this problem, we
will give you a set of relations of the form A < B and ask you to
determine whether a sorted order has been specifed or not.

由一些不同元素组成的升序序列是可以用若干个小于号将所有的
元素按从小到大的顺序 排列起来的序列。例如，排序后的序列
为 A, B, C, D，这意味着 A < B、 B < C 和 C < D。在本题中，
给定一组形如 A < B 的关系式，你的任务是判定是否存在一个
有序序列。输出到哪一项可以确定顺序或者在这一项最先出现冲
突，若所有的小于关系都处理完了都不能确定顺序也没有出现冲
突，就输出不能确定。

>Solution

# 冲突即为出现环

# 确定即为拓扑排序时队中元素不大于 1

每次取队首，队列里只有一个元素，那么顺序唯一确定

# 每次加入新的关系重新拓扑排序一次即可

BZOJ 2200 道路和航线

FJ 正在一个新的销售区域对他的牛奶销售方案进行调查。

他想把牛奶送到 T 个城镇 (1 ≤ T ≤ 25000)，编号为 1 到 T。

这些城镇之间通过 R 条道路 (1 ≤ R ≤ 50000) 和 P 条航线(1 ≤ P ≤ 50000) 连接。

每条道路 i 或者航线 i 连接城镇 Ai 到Bi，花费为 Ci。

对于道路， 0 ≤ Ci ≤ 10000;

然而航线的花费很神奇，花费 Ci 可能是负数 (-10000 ≤ Ci ≤ 10000)。

道路是双向的，可以从 Ai 到 Bi，也可以从 Bi 到 Ai，花费都是 Ci。

然而航线与之不同，只可以从 Ai 到 Bi。

事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策保证：

如果有一条航线可以从 Ai 到 Bi，那么保证不可能通过一些道路和航线从 Bi 回到Ai。

由于 FJ 的奶牛世界公认〸分给力，他需要运送奶牛到每一个城镇。

他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案，或者知道这是不可能的。

>Solution

有向边不在环内，走拓扑排序

任何在环的地方，都是正权无向边，dij，把 topsort 被更新过的点扔进堆里做 dij ，（也可以直接全部所有点都扔进去）

e 

最短路算法

Floyd 

# 基于动态规划， F_k,u,v, 表示使用点 1, 2, . . . , k 时，点 u 到点 v 的最短路

限制中间点前 k 个

# 从小到大枚举 k， u 和 v 之间的最短路要么不经过 k，要么经过 k 一次且除此之外只包含前 k - 1 个点

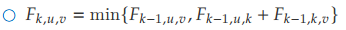
易见，使用二维数组不断覆盖更新即可。

时间复杂度 O(N³)
空间复杂度 O(N²)

可以处理含有负权边的情况，如果含有负环，则存在 i 使得F_i,i < 0。

出现负环，f[i][i] < 0

Floyd 传递闭包，图中任意两点的可达性

如果 i-->k , k->j ，可达，那就更新

玄学剪枝

邻接矩阵初始化

快速幂

Floyd具有矩阵乘法的一些性质，Floyd具有结合律

Dijkstra

适用于没有负权边的图。

# 将所有点分为两个集合，最短路确定的集合 S 和最短路未确定的集合 T，初始 S = {s}

# 求 T 中每个点 v 的当前最短路

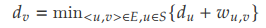
# 取出 T 中 d_v 最小的点，其最短路一定就是 d_v，将其加入 S

# 不断重复上面的操作，直到所有点的最短路都确定

朴素写法时间复杂度较劣，可以采用堆优化至 O((N + M) logN)

>下面是C++11 的写法

下面是个C++98 的写法

// Dijkstra Template (without c++11)
struct data {
    int u;
    int d;
    data(int _u, int _d) :
        u(_u), d(_d) {}
    bool operator < (const data & that) const {
        return d > that.d;
    }//注释1
};

priority_queue<data> heap;

const int inf=0x3f3f3f3f;
void dijkstra(int s) {
    memset(dis, inf, sizeof dis);
    heap.push(data(s, dis[s] = ));
    while (!heap.empty()) {
        data t = heap.top(); heap.pop();
        if (t.d != dis[t.u])continue;   //注释2
        for (int i = hd[t.u], v, w; i; i = nt[i])
            if (v = to[i], w = vl[i], dis[v] > t.d + w)
              //,表达式，最后一个作为返回值
                heap.push(data(v, dis[v] = t.d + w));
    }
}

注释1：

就是重载一个小于号然后按照d从大到小排序

const保险还是加上

注释2：

此处是为了判断点 t.u 有没有更新过别人，更新过就没必要多次更新了

因为你从堆里面取出一个点，用他来更新别的点的最短距离，那么就说明他的最短路径已经被更新过了，是最小的dis[t.u]了

然后对于一个点  v  ，他会被别的点更新 dis[v] ， 可能原来的dis[v]不是最优的，但是他被加到堆里面了，然后后面出现一个更新的新的dis[v]，然后再次更新dis[v]

但是注意priority_queue不支持修改操作，就是对于点 v ，你无法修改他在堆里那个 pair.second ，你只能新建一个data类型的东西，塞到堆里

这样的话，取出 v 来更新别的点的 dis ，那么可能会出现取出原来本应该删除但是由于pq不支持删除而留下的错误dis ，为了防止错误答案更新错误答案，判断一下！！！，如果是个错误答案直接continue掉

Bellman-Ford

// Bellman-Ford

struct edge {
    int u, v, w;
    edge(int _u, int _v, int _w) :
        u(_u), v(_v), w(_w) {}
} e[mxm];

void bellman_ford(int s) {
    memset(dis, inf, sizeof dis);
    dis[s] = ;
    int cnt = , flag = ;
    while (flag) {
        flag = ;
        for (int i = ; i < m; ++i)
            if (dis[e[i].v] > dis[e[i].u] + e[i].w)
                dis[e[i].v] = dis[e[i].u] + e[i].w, flag = ;
    }
    if (++cnt > n) you_fu_huan!!!! break;
}

SPFA

考虑使用队列优化 Bellman-Ford 算法，如果更新了 d_u，则将 u 入队。每次取队首 u 更新其邻点 v 的 d_v。

最坏复杂度 O(NM)

void spfa()
{
    for(int i=;i<=n;i++) { dis[i]=inf;vis[i]=; }
    dis[s]=; vis[s]=;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop(); vis[u]=;
        for(int i=head[u];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(dis[v]>dis[u]+edge[i].dis)
            {
                dis[v]=dis[u]+edge[i].dis;
                if(!vis[v]){ q.push(v); vis[v]=; }
            }
        }
    }
}

判断有没有负环就是，如果一个点入队的次数>n次，那么就说明出现了负环，开个数组记录一下

// SPFA

void spfa(int s) {
    memset(dis, inf, sizeof dis);
    static int que[];
    static bool vis[mxn];
    int l = , r = ;
    dis[que[r++] = s] = ;
    while (l != r) {
        int u = que[l++];
        vis[u] = false;
        for (int i = hd[u], v, w; i; i = nt[i])
            if (v = to[i], w = vl[i], dis[v] > dis[u] + w)
                if (dis[v] = dis[u] + w, !vis[v])
                    vis[que[r++] = v] = true;
    }
}

YouSiki's Code

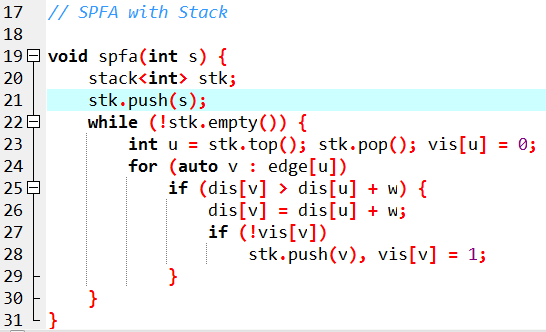
栈更容易判负环