KMP算法的理解

---恢复内容开始---

　　在看数据结构的串的讲解的时候，讲到了KMP算法——一个经典的字符串匹配的算法，具体背景自行百度之，是一个很牛的图灵奖得主和他的学生提出的。

　　一开始看算法的时候很困惑，但是算法思想很简单，就是在暴力匹配的基础上得出的。

暴力匹配

　　这里有必要说一下暴力匹配，暴力匹配更简单，就是按照人的常规思维去匹配字符串，拿模式串（P）的第一个字符去和给定串（S）比较，S从左往右看，一看，第一个，呀~不对，啥也不说了，第一个都不对了，后边还比个毛。所以，这一次比较，S中第一个字符开头是匹配串就不可能了。然后就拿P的第一个字符，去和S中第二个字符开头的比较，一看，对上了，有希望，再往后看，全对上了，恭喜你，程序结束了，没对上，也不要气馁，开始看S的第三个字符开头的字符串……如此一遍遍重复，直到找到匹配串。

　　上述算法暴力，简单，但复杂度高，O（n²）的，一次就找到算你幸运，但是，形如“0000000001”的串S和形如“000001”的匹配起来就麻烦了，每次移动一个，看到P串的最后一个才发现不行，直到P串移动到最后。

KMP

　　那么KMP就解决了这个问题，他让P串不是简单地往后移动一个了，而是移动k个，因为，我们每次比较时，前若干字符在上一次比较中的情况已经知道了，所以我们在下一次比较时，可以利用上一次比较的结果，不用再去做无用功了。

　　那么关键来了，他为什么可以移动k个呀，你怎么保证你在移动k个的时候（略过了移动0~k个），没有把正确答案错过？思前想后，个人觉得，归根结底还是根据模式串P的前缀和后缀的重复性决定的。

　　这里有两个问题要解释

　　（1）前缀和后缀

　　举个栗子，字符串“ababa”　的所有前缀为“a”、“ab”、“aba”、“abab”，就是以第一个字符开头，不包含最后一个字符的所有子串。同理，所有后缀就是“a”、“ba”、“aba”、“baba”，就是以最后一个字符结尾，不包含第一个字符的所有子串。

　　（2）重复性

　　关键来了，我觉得这是能使P向后移动k个而不是1个的基础。

　　

　　以上图所示的匹配为栗子，目前已经匹配了“ababa”（后边的先不看），再往后匹配就失败了，此时我要移动P串，KMP就不是移动一个了，而是移动k个，那么怎么决定k的大小呢，很显然，已经匹配的串的后缀和前缀是有一定重复的，这样利用重复的信息，在向后移动的时候，我们才能把前面一部分直接拿来用。

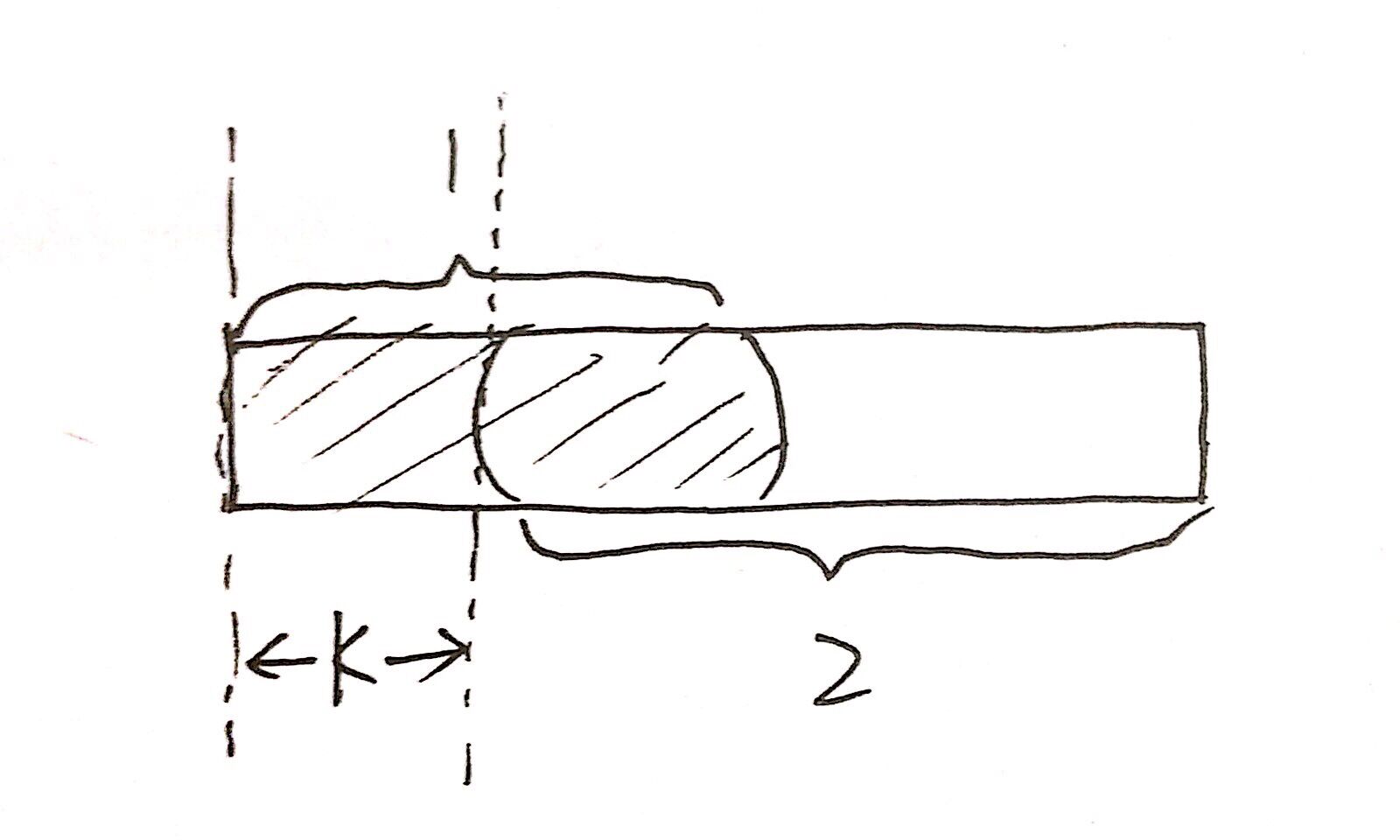
　　就像手绘的这张图一样，整个矩形我们目前已经匹配上了，1部分和2部分是重复的，那么我们就可以向后移动k个，即1和2重合，毫无疑问，移动后，1部分是已经匹配好的，无需再检测匹配了。

　　所以，我们需要找，前缀和后缀最长的公共部分的长度。很显然，公共部分越长，k就越小，说明当前越接近匹配串。为了后边便于操作，我们在预处理中，遍历得到模式串P的所有子串的最大公共部分长度，构成部分匹配表（next表），在后边匹配的时候，直接查表就可以得到下一次前进的k值。

　　例如在上述讲前缀后缀时的栗子，前缀和后缀最长公共部分是“aba”，因此，表中对应的值就是3。

　　当然，前进的k=已经匹配的字符串长度-该串对应的匹配表的值；（k>1时才有意义）

　　

　　行了，我理解的KMP算法已经讲完了，最后举个栗子验证一下

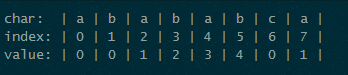
　　用别人的一张图吧，应该没事吧~~~

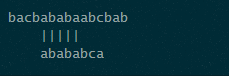
　　这是上边所说的部分匹配表，具体怎么得到的上边已经讲了。模式串P是“abababca”，待查找的串S为“bacbababaabcbab”。

1. p的第一个和S的第一个不匹配，后移，此时那个公式没用，直接向后移动一个。
2. P[0]和S[1]匹配上了，但是P[1]和S[2]不匹配，a对应的值为0，公式没用，直接向后移动一个。
3. 然后跟c和b比较都不行，也是每次移动一个
4. 再往后比较时，P中“ababa”和S中“ababa”匹配成功，再往后，P中是“b”，而S中是“a”，不匹配，此时查“ababa”对应的值是3，“ababa”长度是5，那么向后移动2个，继续比较

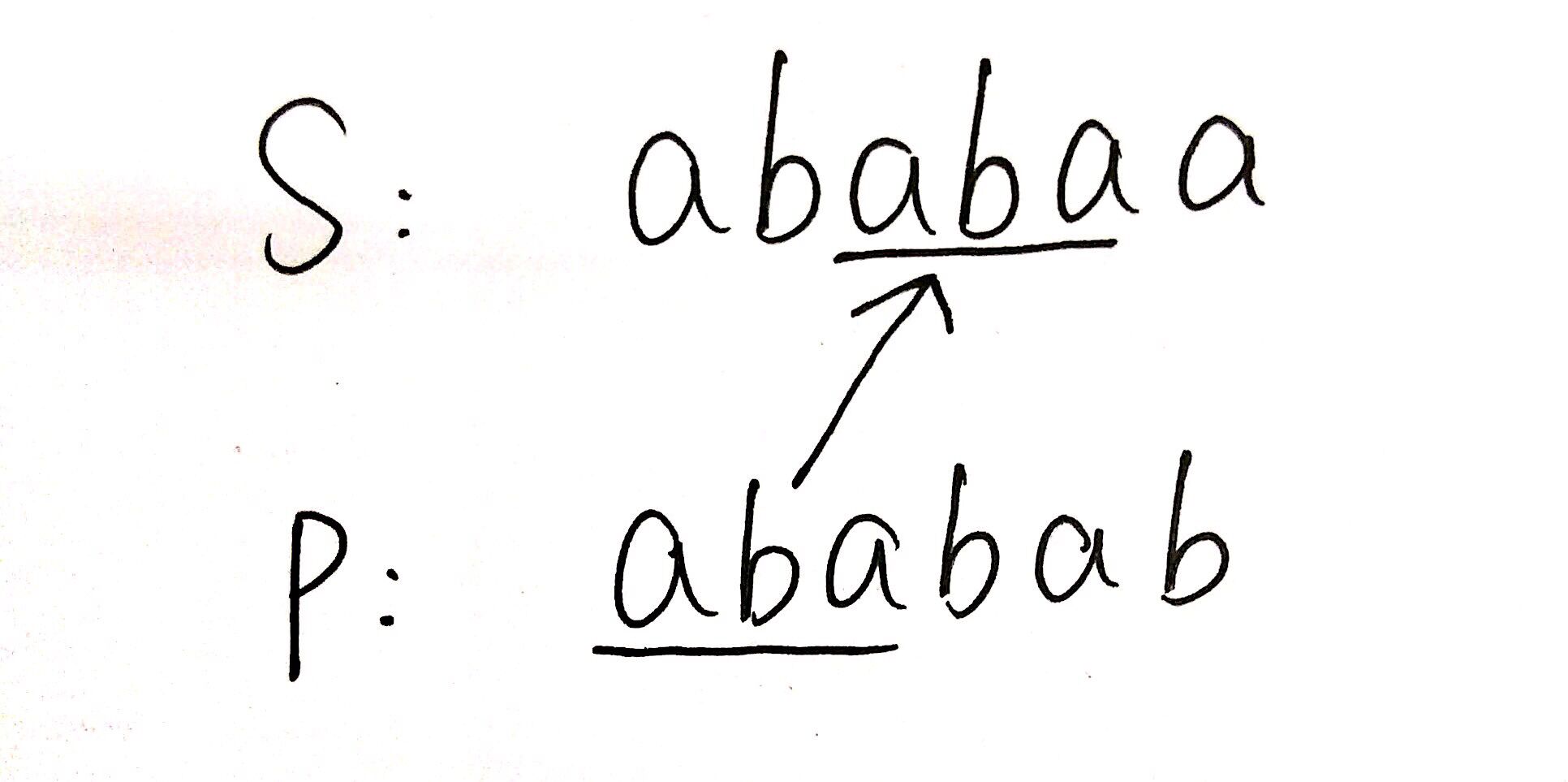
　　如图，画线部分，移动之后依然对其，就不用再比较了。

　　剩下的工作类似，知道找到匹配串或者匹配失败。

　　如下是简单的KMP实现代码

 #include<stdio.h>
 #include<string.h>
 //定义next数组中的元素
 typedef struct Next
 {
     int value;
     char ch;
     int num;
 } Next;
 Next next[];
 int kmp(char *s,char *p)
 {
     int len1 = strlen(s);    //S串
     int len2 = strlen(p);    //模式串
     int i=,j=;
     int pos=i;  //记录每次S中开始比较的位置
     int succ=;
     while(len1-pos>=len2)
     {

         i=pos;
         while(s[i]==p[j]&&j<len2)
         {
             ++i;
             ++j;
         }
         if(j==len2)
         {
             succ=;
             break;
         }
         if(next[j-].value<)
         {
             j=;
             ++pos;
             continue;
         }
         pos=pos+j-next[j-].value;   //S串中跳动的位置
         j=;    //每次模式串从头比较，其实不用。。。
     }
     if(succ==)
         return i-len2;
     else
         return -;
 }
 void getNext(char *p)
 {
     int len;
     int k;
     char pre[],suf[];
     int flag=;
     for(int i=; i<strlen(p); ++i)
     {
         len=i+;
         k=len-;
         flag=;
         next[i].ch=p[i];
         next[i].num=i;
         //从可能的最大的k开始寻找
         while(k!=)
         {
             for(int j=; j<k; ++j)
             {
                 pre[j]=p[j];
                 suf[j]=p[len-k+j];
                 pre[j+]='\0';
                 suf[j+]='\0';
             }
             if(strcmp(pre,suf)==)
             {
                 flag=;
                 break;
             }
             else
                 --k;
         }
         if(flag==)
             next[i].value=k;
         else
             next[i].value=;
     }
 }
 int main()
 {
     char s[],p[];
     gets(s);
     gets(p);
     getNext(p);
     int re = kmp(s,p);
     if(re==-)
         printf("Fail\n",re);
     else
         printf("The substring is from %d to %d\n",re,re+strlen(p)-);
     return ;
 }