LeetCode初体验—twoSum

今天注册了大名鼎鼎的LeetCode,做了一道最简单的算法题目：

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution.

Example:

Given nums = [2, 7, 11, 15], target = 9,

Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

UPDATE (2016/2/13):

The return format had been changed to zero-based indices. Please read the above updated description carefully.

Subscribe to see which companies asked this question

虽然题目很简单，但是在做的过程中暴露的问题也是比较多的。

1.多年不碰英语，题目看不懂，很多细节没有理解（例如给定的序列中的数字是不是可以重复、以及序列的长度等）

2.由于没有做过类似的网上直接运行提交的题目，所以一时间不会搞

3.用惯了VS的只能提示，导致直接写代码的时候字母的大小写经常错误

4.可能导致程序崩溃的条件不加，例如这个题目，明显在输入的数组的长度小于2时候可以直接返回

我的程序：

public class Solution {
    public int[] TwoSum(int[] nums, int target) {
        ];
        )
        {
            return temp;
        }
        ;i<=nums.Length - ;i++){
            ;j<=nums.Length - ;j++){
                if((nums[i] + nums[j] == target)){
                    temp[] = i;
                    temp[] = j;
                    return temp;
                }
            }
        }
        return temp;
    }
}

做完提交后会有一个性能分析和排名：

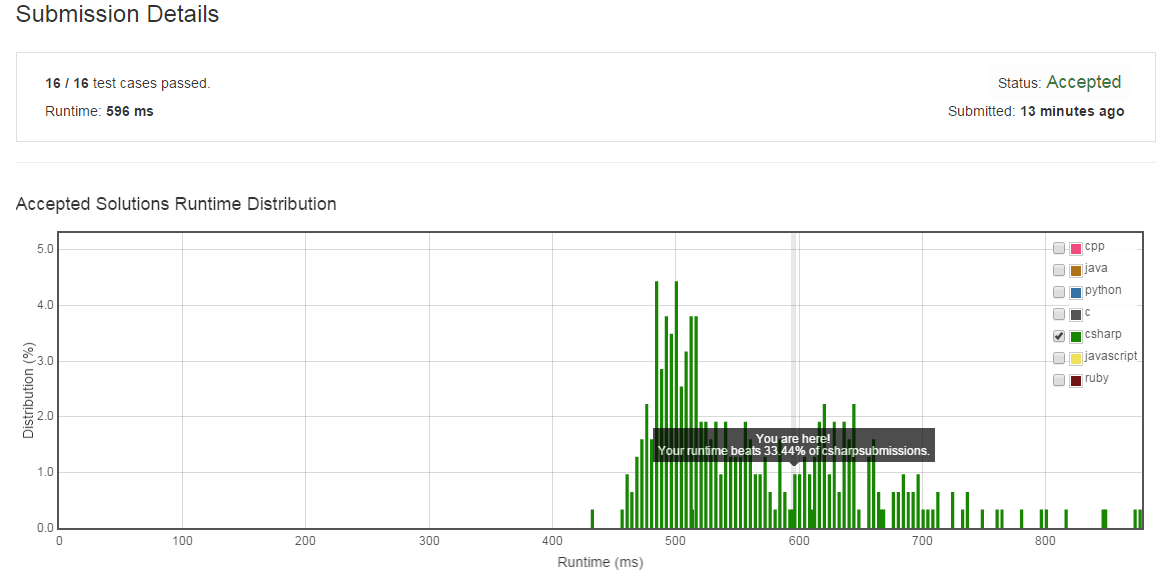
通过上面可以看到我的计算方法的效率，说明有60%多的算法比我这个效率要高，所以可以看看人家是怎么做的：

查看算法的讲解，有一种方法是采用了哈希表的方式，我上面的方式采用的是暴力搜索的方式，时间复杂度O(n​²​​)，而采用哈希的方式是O(n)

Approach #2 (Two-pass Hash Table) [Accepted]

To improve our run time complexity, we need a more efficient way to check if the complement exists in the array. If the complement exists, we need to look up its index. What is the best way to maintain a mapping of each element in the array to its index? A hash table.

We reduce the look up time from O(n)O(n) to O(1)O(1) by trading space for speed. A hash table is built exactly for this purpose, it supports fast look up in nearconstant time. I say "near" because if a collision occurred, a look up could degenerate to O(n)O(n) time. But look up in hash table should be amortized O(1)O(1) time as long as the hash function was chosen carefully.

A simple implementation uses two iterations. In the first iteration, we add each element's value and its index to the table. Then, in the second iteration we check if each element's complement (target - nums[i]target−nums[i]) exists in the table. Beware that the complement must not be nums[i]nums[i] itself!

public int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        map.put(nums[i], i);
    }
    for (int i = 0; i < nums.length; i++) {
        int complement = target - nums[i];
        if (map.containsKey(complement) && map.get(complement) != i) {
            return new int[] { i, map.get(complement) };
        }
    }
    throw new IllegalArgumentException("No two sum solution");
}

Complexity Analysis:

• Time complexity : O(n)O(n). We traverse the list containing nn elements exactly twice. Since the hash table reduces the look up time to O(1)O(1), the time complexity is O(n)O(n).

• Space complexity : O(n)O(n). The extra space required depends on the number of items stored in the hash table, which stores exactly nn elements.

思路有了，用C#去改写

        public int[] TwoSum(int[] nums, int target)
        {
            if (nums.Length < 2)
            {
                throw new Exception();
            }
            Dictionary<int, int> dict = new Dictionary<int, int>();
            for (int i = 0; i <= nums.Length - 1; i++)
            {
                dict.Add(i, nums[i]);
            }
            for (int i = 0; i <= nums.Length - 1; i++)
            {
                int temp = target - nums[i];

                if (dict.ContainsValue(temp) && dict.FirstOrDefault(q => q.Value == temp).Key != i)
                {
                    return new int[] { dict.FirstOrDefault(q => q.Value == temp).Key, i };
                }
            }
            throw new Exception();
        }

但是在提交的时候出现了问题：

超时了！！！！

和大神们讨论了一下也没发现什么问题。

还有一种是这个变种：

Approach #3 (One-pass Hash Table) [Accepted]

public int[] twoSum(int[] nums, int target) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        int complement = target - nums[i];
        if (map.containsKey(complement)) {
            return new int[] { map.get(complement), i };
        }
        map.put(nums[i], i);
    }
    throw new IllegalArgumentException("No two sum solution");
}

就是把上面的两次循环，变成了一次循环，把先构建哈希表变成了后构建，每次循环时候去看是否存在。

偶然发现有人这么写的，于是就扒下来看了一下：

public int[] TwoSum(int[] nums, int target)
{
    int numsLength = nums.Length;
)
    {
         return nums;
    }
    ];
    var numsInDictionary = new Dictionary<int, int>();

    ; i < numsLength; i++)
    {
        if (numsInDictionary.ContainsKey(target - nums[i]))
        {
             result[] = i;
             result[] = numsInDictionary[target - nums[i]];
             break;
        }
        if (!numsInDictionary.ContainsKey(nums[i]))
        {
             numsInDictionary.Add(nums[i], i);
        }
    }
    return result;
}