Java 源码刨析 - HashMap 底层实现原理是什么？JDK8 做了哪些优化？

【基本结构】

在 JDK 1.7 中 HashMap 是以数组加链表的形式组成的；

JDK 1.8 之后新增了红黑树的组成结构，当链表大于 8 并且容量大于 64 时，链表结构会转换成红黑树结构，它的组成结构如下图所示：

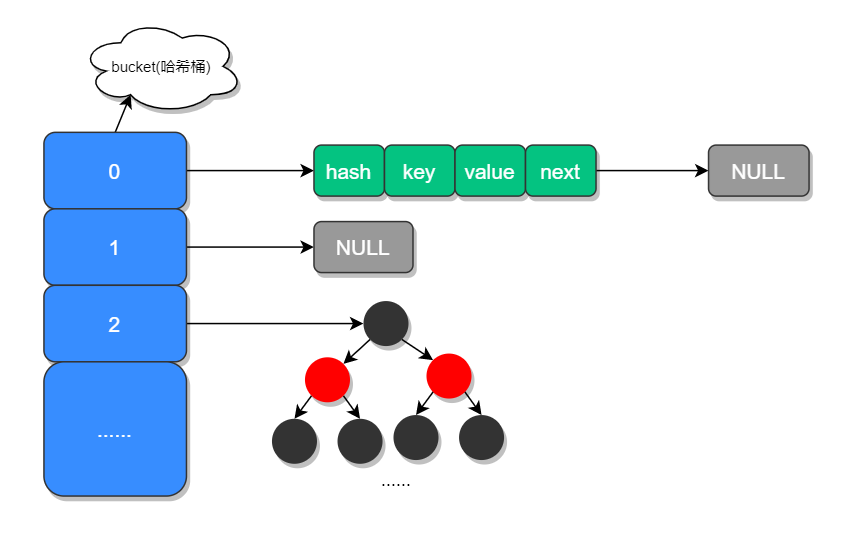
数组中的元素我们称之为哈希桶，它的定义如下：

static class Node<K,V> implements Map.Entry<K,V> {

final int hash;

final K key;

V value;

Node<K,V> next;

Node(int hash, K key, V value, Node<K,V> next) {

this.hash = hash;

this.key = key;

this.value = value;

this.next = next;

}

public final K getKey()        { return key; }

public final V getValue()      { return value; }

public final String toString() { return key + "=" + value; }

public final int hashCode() {

return Objects.hashCode(key) ^ Objects.hashCode(value);

}

public final V setValue(V newValue) {

V oldValue = value;

value = newValue;

return oldValue;

}

public final boolean equals(Object o) {

if (o == this)

return true;

if (o instanceof Map.Entry) {

Map.Entry<?,?> e = (Map.Entry<?,?>)o;

if (Objects.equals(key, e.getKey()) &&

Objects.equals(value, e.getValue()))

return true;

}

return false;

}

}

可以看出每个哈希桶中包含了四个字段：hash、key、value、next，其中 next 表示链表的下一个节点。

JDK 1.8 之所以添加红黑树是因为一旦链表过长，会严重影响 HashMap 的性能，而红黑树具有快速增删改查的特点，这样就可以有效的解决链表过长时操作比较慢的问题。

【HashMap 源码分析】

HashMap 源码中包含了以下几个属性：

// HashMap 初始化长度

static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

// HashMap 最大长度

static final int MAXIMUM_CAPACITY = 1 << 30; // 1073741824

// 默认的加载因子 (扩容因子)

static final float DEFAULT_LOAD_FACTOR = 0.75f;

// 当链表长度大于此值且容量大于 64 时

static final int TREEIFY_THRESHOLD = 8;

// 转换链表的临界值，当元素小于此值时，会将红黑树结构转换成链表结构

static final int UNTREEIFY_THRESHOLD = 6;

// 最小树容量

static final int MIN_TREEIFY_CAPACITY =

【什么是加载因子？加载因子为什么是 0.75？】

加载因子也叫扩容因子或负载因子，用来判断什么时候进行扩容的，假如加载因子是 0.5，HashMap 的初始化容量是 16，那么当 HashMap 中有 16*0.5=8 个元素时，HashMap 就会进行扩容。

那加载因子为什么是 0.75 而不是 0.5 或者 1.0 呢？

这其实是出于容量和性能之间平衡的结果：

当加载因子设置比较大的时候，扩容的门槛就被提高了，扩容发生的频率比较低，占用的空间会比较小，但此时发生 Hash 冲突的几率就会提升，因此需要更复杂的数据结构来存储元素，这样对元素的操作时间就会增加，运行效率也会因此降低；

而当加载因子值比较小的时候，扩容的门槛会比较低，因此会占用更多的空间，此时元素的存储就比较稀疏，发生哈希冲突的可能性就比较小，因此操作性能会比较高。

所以综合了以上情况就取了一个 0.5 到 1.0 的平均数 0.75 作为加载因子。

【查询源码】

public V get(Object key) {

Node<K,V> e;

// 对 key 进行哈希操作

return (e = getNode(hash(key), key)) == null ? null : e.value;

}

final Node<K,V> getNode(int hash, Object key) {

Node<K,V>[] tab; Node<K,V> first, e; int n; K k;

// 非空判断

if ((tab = table) != null && (n = tab.length) > 0 &&

(first = tab[(n - 1) & hash]) != null) {

// 判断第一个元素是否是要查询的元素

if (first.hash == hash && // always check first node

((k = first.key) == key || (key != null && key.equals(k))))

return first;

// 下一个节点非空判断

if ((e = first.next) != null) {

// 如果第一节点是树结构，则使用 getTreeNode 直接获取相应的数据

if (first instanceof TreeNode)

return ((TreeNode<K,V>)first).getTreeNode(hash, key);

do {

// 非树结构，循环节点判断

// hash 相等并且 key 相同，则返回此节点

if (e.hash == hash &&

((k = e.key) == key || (key != null && key.equals(k))))

return e;

} while ((e = e.next) != null);

}

}

return null;

}

从以上源码可以看出，当哈希冲突时我们需要通过判断 key 值是否相等，才能确认此元素是不是我们想要的元素。

【新增源码】

public V put(K key, V value) {

// 对 key 进行哈希操作

return putVal(hash(key), key, value, false, true);

}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,

boolean evict) {

Node<K,V>[] tab; Node<K,V> p; int n, i;

// 哈希表为空则创建表

if ((tab = table) == null || (n = tab.length) == 0)

n = (tab = resize()).length;

// 根据 key 的哈希值计算出要插入的数组索引 i

if ((p = tab[i = (n - 1) & hash]) == null)

// 如果 table[i] 等于 null，则直接插入

tab[i] = newNode(hash, key, value, null);

else {

Node<K,V> e; K k;

// 如果 key 已经存在了，直接覆盖 value

if (p.hash == hash &&

((k = p.key) == key || (key != null && key.equals(k))))

e = p;

// 如果 key 不存在，判断是否为红黑树

else if (p instanceof TreeNode)

// 红黑树直接插入键值对

e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);

else {

// 为链表结构，循环准备插入

for (int binCount = 0; ; ++binCount) {

// 下一个元素为空时

if ((e = p.next) == null) {

p.next = newNode(hash, key, value, null);

// 转换为红黑树进行处理

if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st

treeifyBin(tab, hash);

break;

}

//  key 已经存在直接覆盖 value

if (e.hash == hash &&

((k = e.key) == key || (key != null && key.equals(k))))

break;

p = e;

}

}

if (e != null) { // existing mapping for key

V oldValue = e.value;

if (!onlyIfAbsent || oldValue == null)

e.value = value;

afterNodeAccess(e);

return oldValue;

}

}

++modCount;

// 超过最大容量，扩容

if (++size > threshold)

resize();

afterNodeInsertion(evict);

return null;

}

新增方法的执行流程，如下图所示：

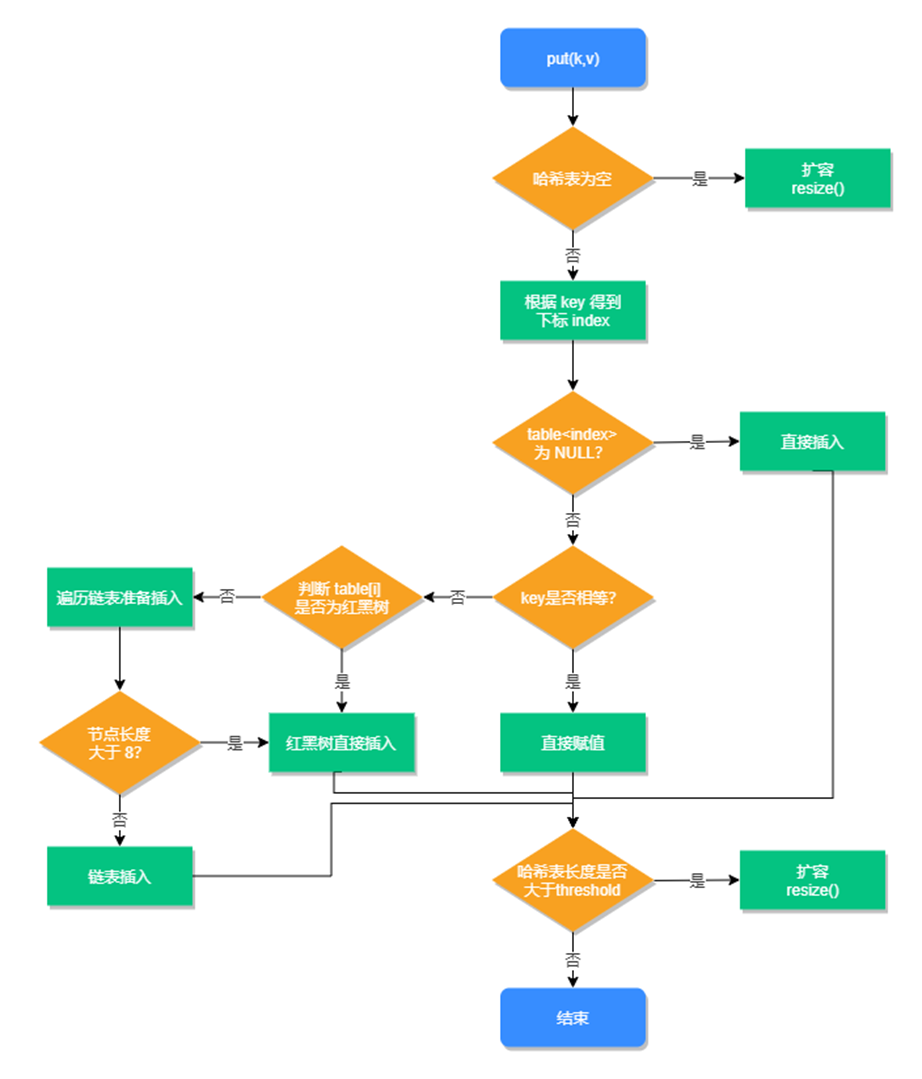
【扩容源码】

final Node<K,V>[] resize() {

// 扩容前的数组

Node<K,V>[] oldTab = table;

// 扩容前的数组的大小和阈值

int oldCap = (oldTab == null) ? 0 : oldTab.length;

int oldThr = threshold;

// 预定义新数组的大小和阈值

int newCap, newThr = 0;

if (oldCap > 0) {

// 超过最大值就不再扩容了

if (oldCap >= MAXIMUM_CAPACITY) {

threshold = Integer.MAX_VALUE;

return oldTab;

}

// 扩大容量为当前容量的两倍，但不能超过 MAXIMUM_CAPACITY

else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&

oldCap >= DEFAULT_INITIAL_CAPACITY)

newThr = oldThr << 1; // double threshold

}

// 当前数组没有数据，使用初始化的值

else if (oldThr > 0) // initial capacity was placed in threshold

newCap = oldThr;

else {               // zero initial threshold signifies using defaults

// 如果初始化的值为 0，则使用默认的初始化容量

newCap = DEFAULT_INITIAL_CAPACITY;

newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);

}

// 如果新的容量等于 0

if (newThr == 0) {

float ft = (float)newCap * loadFactor;

newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?

(int)ft : Integer.MAX_VALUE);

}

threshold = newThr;

@SuppressWarnings({"rawtypes","unchecked"})

Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];

// 开始扩容，将新的容量赋值给 table

table = newTab;

// 原数据不为空，将原数据复制到新 table 中

if (oldTab != null) {

// 根据容量循环数组，复制非空元素到新 table

for (int j = 0; j < oldCap; ++j) {

Node<K,V> e;

if ((e = oldTab[j]) != null) {

oldTab[j] = null;

// 如果链表只有一个，则进行直接赋值

if (e.next == null)

newTab[e.hash & (newCap - 1)] = e;

else if (e instanceof TreeNode)

// 红黑树相关的操作

((TreeNode<K,V>)e).split(this, newTab, j, oldCap);

else { // preserve order

// 链表复制，JDK 1.8 扩容优化部分

Node<K,V> loHead = null, loTail = null;

Node<K,V> hiHead = null, hiTail = null;

Node<K,V> next;

do {

next = e.next;

// 原索引

if ((e.hash & oldCap) == 0) {

if (loTail == null)

loHead = e;

else

loTail.next = e;

loTail = e;

}

// 原索引 + oldCap

else {

if (hiTail == null)

hiHead = e;

else

hiTail.next = e;

hiTail = e;

}

} while ((e = next) != null);

// 将原索引放到哈希桶中

if (loTail != null) {

loTail.next = null;

newTab[j] = loHead;

}

// 将原索引 + oldCap 放到哈希桶中

if (hiTail != null) {

hiTail.next = null;

newTab[j + oldCap] = hiHead;

}

}

}

}

}

return newTab;

}

从以上源码可以看出，JDK 1.8 在扩容时并没有像 JDK 1.7 那样，重新计算每个元素的哈希值，而是通过高位运算（e.hash & oldCap）来确定元素是否需要移动，比如 key1 的信息如下：

key1.hash = 10 0000 1010

oldCap = 16 0001 0000

使用 e.hash & oldCap 得到的结果，高一位为 0，当结果为 0 时表示元素在扩容时位置不会发生任何变化，而 key 2 信息如下：

key2.hash = 10 0001 0001

oldCap = 16 0001 0000

这时候得到的结果，高一位为 1，当结果为 1 时，表示元素在扩容时位置发生了变化，新的下标位置等于原下标位置 + 原数组长度，如下图所示：

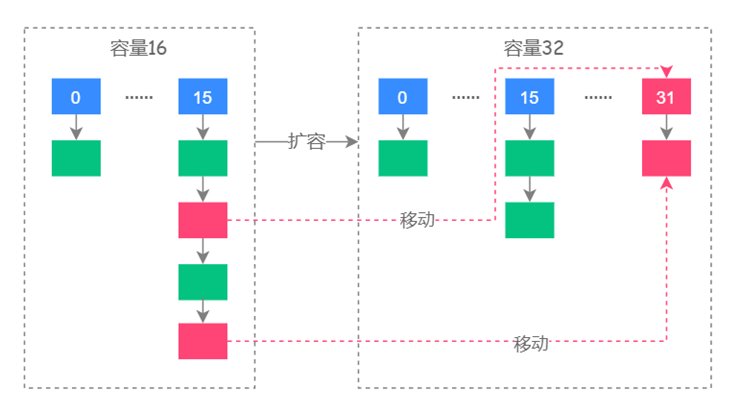
其中红色的虚线图代表了扩容时元素移动的位置。

【HashMap 死循环分析】

以 JDK 1.7 为例，假设 HashMap 默认大小为 2，原本 HashMap 中有一个元素 key(5)；

我们再使用两个线程：t1 添加元素 key(3)，t2 添加元素 key(7)；

当元素 key(3) 和 key(7) 都添加到 HashMap 中之后，线程 t1 在执行到 Entry<K,V> next = e.next; 时，交出了 CPU 的使用权，源码如下：

void transfer(Entry[] newTable, boolean rehash) {

int newCapacity = newTable.length;

for (Entry<K,V> e : table) {

while(null != e) {

Entry<K,V> next = e.next; // 线程一执行此处

if (rehash) {

e.hash = null == e.key ? 0 : hash(e.key);

}

int i = indexFor(e.hash, newCapacity);

e.next = newTable[i];

newTable[i] = e;

e = next;

}

}

}

那么此时线程 t1 中的 e 指向了 key(3)，而 next 指向了 key(7) ；之后线程 t2 重新 rehash 之后链表的顺序被反转，链表的位置变成了 key(5) → key(7) → key(3)，其中 "→" 用来表示下一个元素。

当 t1 重新获得执行权之后，先执行 newTalbe[i] = e 把 key(3) 的 next 设置为 key(7)，而下次循环时查询到 key(7) 的 next 元素为 key(3)，于是就形成了 key(3) 和 key(7) 的循环引用，因此就导致了死循环的发生，如下图所示：

当然发生死循环的原因是 JDK 1.7 链表插入方式为首部倒序插入，这个问题在 JDK 1.8 得到了改善，变成了尾部正序插入。

有人曾经把这个问题反馈给了 Sun 公司，但 Sun 公司认为这不是一个问题，因为 HashMap 本身就是非线程安全的，如果要在多线程下，建议使用 ConcurrentHashMap 替代，但这个问题在面试中被问到的几率依然很大，所以在这里需要特别说明一下。

from：Java 源码剖析（https://kaiwu.lagou.com/course/courseInfo.htm?courseId=59#/detail/pc?id=1761）