P3381 【模板】最小费用最大流（MCMF）

P3381 【模板】最小费用最大流

题目描述 如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入格式 第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

输出格式 一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

输入输出样例

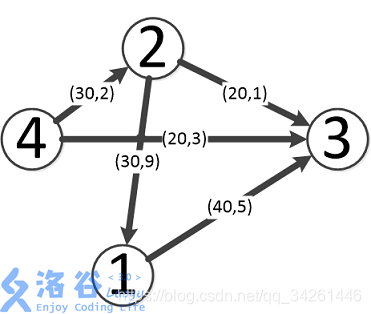
输入 #1 复制
4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5
输出 #1 复制
50 280

说明/提示 时空限制：1000ms,128M

（BYX：最后两个点改成了1200ms）

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

如图，最优方案如下：

第一条流为4–>3，流量为20，费用为3*20=60。

第二条流为4–>2–>3，流量为20，费用为（2+1）*20=60。

第三条流为4–>2–>1–>3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

思路

Spfa + Dinic

题解如下

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
#define INF 0x3f3f3f3f
#define ll long long
const int maxn = 5005;
const int maxm = 150000;
int n, m, s, e;
struct Edge
{
    int v, w, cap, next;
} edge[maxm];
int head[maxn], dis[maxn], use[maxn];
int pre[maxn], last[maxm];      //pre 是用来存储上一个节点的， 而last 则是存储上一个边
int flow[maxn];
int k = -1;
ll mx_flw = 0, mn_cst = 0;
void Add(int u, int v, int w, int cap)
{
    edge[++ k] = (Edge){ v, w, cap, head[u]}; head[u] = k;
    edge[++ k] = (Edge){ u, -w, 0, head[v]};  head[v] = k;
}
bool Spfa(int s, int e)
{
    int ar[10];
    for(int i = 0; i <= n; i ++)
        dis[i] = INF, use[i] = 0, flow[i] = INF;
    dis[s] = 0;
    queue<int> q;
    q.push(s);
    int u,v,w;
    while(! q.empty())
    {
        u = q.front(); q.pop();
        use[u] = 0;
        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            v = edge[i].v;
            w = edge[i].w;
            if(edge[i].cap && dis[v] > dis[u] + w)
            {
                dis[v] = dis[u] + w;
                pre[v] = u;
                last[v] = i;
                flow[v] = min(flow[u], edge[i].cap);
                if(! use[v])
                {
                    q.push(v);
                    use[v] = 1;
                }
            }
        }
    }
    if(flow[e] != INF)
        return true;
    return false;
}
void MCMF(int s, int e)
{
    while(Spfa(s, e))
    {
        mx_flw += flow[e];
        mn_cst += flow[e]*1LL * dis[e]*1LL;
        int now = e;
        while(now != s)     //更新 残量
        {
            edge[last[now]].cap -= flow[e];
            edge[last[now]^1].cap += flow[e];
            now = pre[now];
        }
    }
}
void init()
{
    k = -1;
    for(int i = 0; i <= n; i ++)
        head[i] = -1;
    mx_flw = 0, mn_cst = 0;
}
int main()
{
    ios::sync_with_stdio(false); cin.tie(0);
    //freopen("T.txt","r",stdin);
    while(cin >> n >> m >> s >> e)
    {
        init();
        int u, v, cap, w;
        for(int i = 1; i <= m; i ++)
            cin >> u >> v >> cap >> w, Add(u, v, w, cap);
        MCMF(s, e);
        cout << mx_flw << " " << mn_cst << endl;
    }
    return 0;
}