题解【[CQOI2017]小Q的棋盘】

切了水题十分快乐~

首先发现本题结构一定是颗树~

本题样例1：

。。没啥用？

样例2：

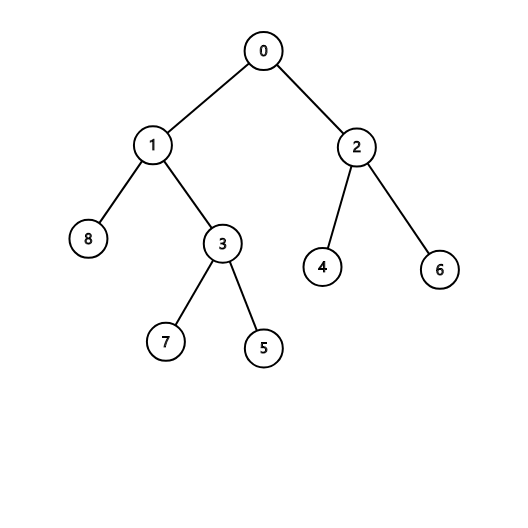
这个时候我们发现：根据贪心思想我们希望每次走一步都多走一个点，如果我们选择最长链的话，在链上每走一步就多走了一个点，如果走不完最长链，那答案就是步数+1，而如果走完最长链还有剩余步数的话，每两步可以多访问一个节点，除非已经访问过所有节点。

接下来证明而如果走完最长链还有剩余步数的话，每两步可以多访问一个节点 ：

\[\text{设走过的集合为}S_1\text{，没走到的集合为}S_2\text{，点集为}V\text{，边集为}E\]

\[\text{那么当}S_1 \neq V\text{时，至少存在一点U，其子节点中至少有一个属于}S_2\]

\[\text{因为如果不存在这样的结点，该图就不是联通图，更别说树了}\]

\[\text{那么在访问该节点时，可以花费一步访问那个儿子，在花费一步回来继续}\]

\[\text{所以走完最长链还有剩余步数的话，每两步可以多访问一个节点}\]

那么就是道水题啦~ 建议大家去luogu评个红~

图片来源：http://bubbleioa.top