[CEOI1999]Parity Game 题解

P5937 [CEOI1999]Parity Game

洛谷P5937 P5937 [CEOI1999]Parity Game

---

前言：

个人感觉这道题初看想不到并查集啊！（说实话我题都没读懂，第二遍才读懂）

好了，转入正题，这道题我们可以用两种方法A掉：种类并查集&带权并查集

---

题目简述：

给定01序列的长度n，询问和答案的个数m

对于每行的询问和回答先给出两个整数，表示询问区间（闭区间）

再给出一个字符串回答：“odd”表示区间有奇数个1，“even”表示区间有偶数个1

如果存在一个01序列满足第1个到第x个的回答，不满足第x+1个回答，则输出x（如果m个回答都满足，那肯定就输出m）

数据范围：

对于100%的数据，1≤N≤10^9，1≤M≤5×10^3

因为N有点大，所以我们需要使用到离散化！ 来将大数据映射到小范围的小数据

---

引入：

其实本题和程序自动分析这道题很像：都是给定若干个变量和关系，判断这些关系的可满足性问题

不过我们这道题的传递关系不止一种（涉及到了奇偶性）：

1. 若x1与x2的奇偶性相同，x2与x3的奇偶性相同，那么x1与x3的奇偶性相同

2. 若x1与x2的奇偶性相同，x2与x3的奇偶性不同，那么x1与x3的奇偶性不同

3. 若x1与x2的奇偶性不同，x2与x3的奇偶性不同，那么x1与x3的奇偶性不同

---

种类并查集：

（因为我认为这道题种类并查集比较好想也比较好理解，所以先讲种类并查集的做法ovo，下面通过问答的形式给出思路）

• 为什么想到种类并查集？

1. 本题需要记录与自己相同的和不同的，那么我们可以将相同的理解为“朋友”，将不同的理解为“敌人”

2. 而题目中的奇偶性又具有传递性（见上“引入部分”），所以我们还需要维护这种传递性——于是我们想到了种类并查集

• 怎么维护传递性&怎么判断回答是否正确？

1. 每遇到一个回答，我们先判断当前两个区间端点的奇偶性：

①对于“even”回答，若左端点在右端点“敌人”的集合中或右端点在左端点“敌人”的集合中，则回答错误

②对于“odd”回答，若左端点在右端点“朋友”的集合中或右端点在左端点“朋友”的集合中，则回答错误

1. 如果回答是正确的，那我们就进行合并操作：

①对于“even”，我们将左端点和右端点的“朋友”、“敌人”集合分别合并

②对于“odd”，我们将左端点的“朋友”与右端点的“敌人”合并，将左端点的“敌人”与右端点的“朋友”合并

• 怎么离散化？

可见浅谈离散化这篇博客qvq

• 下面给出种类并查集做法的完整代码：

#include <bits/stdc++.h>
using namespace std;
int n,m,tot,res,b[100010],fa[100010];

struct node {
	int u,v;
	string op;
} a[100010];

inline int find(int x) {
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}

int main() {
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=m;i++) {
		scanf("%d%d",&a[i].u,&a[i].v);
		cin>>a[i].op;
		b[++tot]=a[i].u;
		b[++tot]=a[i].v;
	}
	sort(b+1,b+1+tot);
	res=unique(b+1,b+1+tot)-(b+1);
	for(register int i=1;i<=m;i++) {  //STL实现离散化的三部曲
		a[i].u=lower_bound(b+1,b+1+res,a[i].u-1)-b;
		a[i].v=lower_bound(b+1,b+1+res,a[i].v)-b;
	}
	for(register int i=1;i<=2*res;i++) fa[i]=i;
	for(register int i=1;i<=m;i++) {
		if(a[i].op=="even") {  //如果回答是偶数个
			if(find(a[i].u)==find(a[i].v+res)||find(a[i].u+res)==find(a[i].v)) {  //判断奇偶性
				printf("%d",i-1);  //注意是i-1而不是i
				return 0;
			}
			fa[find(a[i].u)]=find(a[i].v);
			fa[find(a[i].u+res)]=find(a[i].v+res);
		}
		else {
			if(find(a[i].u)==find(a[i].v)||find(a[i].u+res)==find(a[i].v+res)) {
				printf("%d",i-1);
				return 0;
			}
			fa[find(a[i].u)]=find(a[i].v+res);
			fa[find(a[i].u+res)]=find(a[i].v);
		}
	}
	printf("%d",m);
	return 0;
}

---

带权并查集：

• 怎么想到带权并查集？

我们不妨将区间转换为一棵树，然后用0/1来表示边权，如下草图：

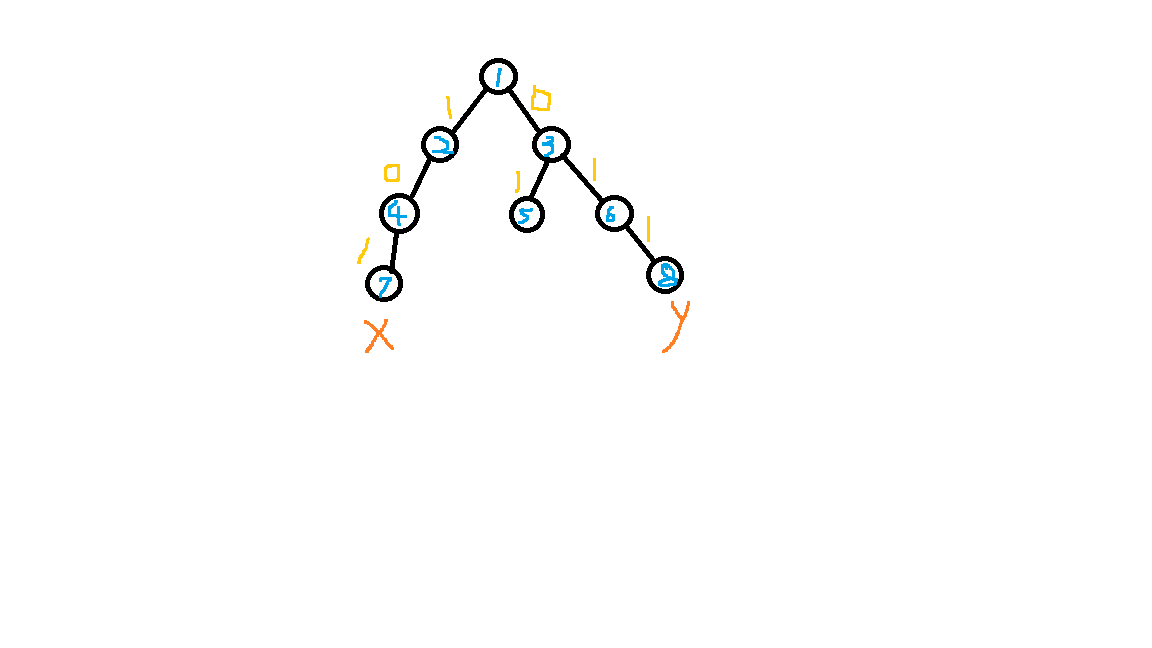
我们可以发现，任意区间都可在在树上表示并求得区间的奇偶性（0/1连成字符串就好）

• 怎么转换为维护带权并查集？

1. 我们将输入中的回答转换为0或1存储：“even”标记为0，“odd”标记为1

2. 我们用dis[x]来记录x与fa[x]的奇偶性关系：为0就相同，反之不同

3. 在路径压缩时，对x到根节点路径上的所有边权做异或（xor）运算，就可以得到x与root的奇偶性关系（都是0/1，所以想到异或）

如上图：dis[x]=1 xor 0 xor 1=0，dis[y]=0 xor 1 xor 1=0

1. 对于每个问题，先检查左右端点是否在同一个集合内（奇偶性是否已知）：

①在的话就计算dis[l] xor dis[r]（即两端点的奇偶性关系），若与回答相矛盾（dis[l] xor dis[r]≠ans），那么回答错误

②不在的话就进行合并操作。此时设两个集合的树根为xl、xr，令xl作为xr的孩子，那就要求出dis[xl]=dis[l] xor dis[r] xor ans

• 下面给出带权并查集做法的完整代码：

#include <bits/stdc++.h>
using namespace std;
string s;
int n,m,tot,res;
int b[100010],fa[100010],dis[100010];

struct node {
	int u,v,op;
} a[100010];

inline int find(int x) {
	if(fa[x]==x) return x;
	int root=find(fa[x]);
	dis[x]^=dis[fa[x]];  //路径压缩求出x与树根的奇偶性关系
	return fa[x]=root;
}

int main() {
	scanf("%d%d",&n,&m);
	for(register int i=1;i<=m;i++) {
		scanf("%d%d",&a[i].u,&a[i].v);
		cin>>s;
		if(s=="even") a[i].op=0;  //转换回答
		else a[i].op=1;
		b[++tot]=a[i].u;
		b[++tot]=a[i].v;
	}
	sort(b+1,b+1+tot);
	res=unique(b+1,b+1+tot)-(b+1);
	for(register int i=1;i<=2*res;i++) fa[i]=i;
	for(register int i=1;i<=m;i++) {
		int x=lower_bound(b+1,b+1+res,a[i].u-1)-b;  //直接判断一个取一个，就不用单独处理
		int y=lower_bound(b+1,b+1+res,a[i].v)-b;
		int xx=find(x),yy=find(y);
		if(xx==yy) {  //在一个集合中
			if((dis[x]^dis[y])!=a[i].op) {  //判断回答是否正确
				printf("%d",i-1);
				return 0;
			}
		}
		else {
			fa[xx]=yy;
			dis[xx]=dis[x]^dis[y]^a[i].op;  //求左端点树根成为右端点树根孩子后的边权
		}
	}
	printf("%d",m);
	return 0;
}

---

然后，感谢一下我的同桌给我的指导

最后，有什么问题欢迎各位dalao们指出来qwq

---