嗨! Apriori算法

Association Rule

一：项集和规则

1.1 认识名词:

Association Rule : 关联规则
Frequent Itemsets : 频繁项集
Sequential Patterns: 模式序列

我们在网上购物的时候,经常会遇到这样的推送, 比如买了A书的人, 同时购买了B书的情景, 在这个描述中: 包含如下的信息:

A书B书经常同时被购买: 频繁项集
买了A书的人,经常会去购买B书: 关联规则

1.2 什么是项集?

比如用购物车的例子来说, 购物车里面的每一件item都叫做一个项, 辣条是一个项, 薯片也是一个项, 所有的商品加起来叫做项集记作itemset，如果有多件商品记作 k-itemset

1.3 什么是Transaction？

transaction就是一组非空的 item的集合，可以把它想成是购物时的小票。

1.4 什么是数据库？

多个 transaction 记录的总和称为 dataset

1.5 什么是关联规则？

关联规则的定义如上公式：

这样理解：就是验证一下P到Q之间有什么关系，其中P属于itemset ，Q也属于itemiset，并且P并不是Q

比如：P是牙刷，Q是牙膏，牙刷和牙膏都是商品，并且牙膏并不是牙刷，我们要做的就是推导出牙膏和牙刷之间之间被用户购买的rule

1.6 什么是Lk Ck?

Lk表示有k个元素的频繁项集

CK表示有K个元素的候选项集, 既然是候选项集, 意味着它里面的元素很可能存在不满足场景规定的支持度大小, 需要被丢弃掉 (什么是支持度? 往下看...)

关联规则有何应用？

Cross Selling: 交叉销售, 比如很经典的数据挖掘问题, 购买啤酒的人通常会购买尿布 , 商家知道这个规则后就可以将这两个商品放在一起, 方便了购物者, 也能起到提醒的作用, 提高营业额。

二：支持度与置信度

介绍数据挖掘中的两个重要概念：

itemset的支持度（Support）

**公式: **

**含义: **Support就是频率的意思，比如说牛奶的支持度，比如一共10个人，其中3个人买了牛奶，那么牛奶的支持度就是3/10 , 它是个比例。如果物品的支持度低，很可能会被忽略不计
关联规则的支持度

**公式: **

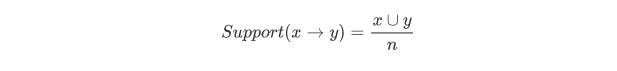
含义: 关联规则的支持度，说的其实也是频率，即同时购买X和Y的订单数量，占全部订单数量的百分比
置信度（Confidence）

公式:

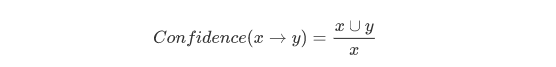
含义: 什么是置信度？比如X=牛奶， Y=面包。置信度就是同时购买牛奶和面包的人, 占购买面包的数量

实际上它描述的就是我们原来学过的条件概率P(Y|X) =P(Y*X) / P(X) ，这个公式至少高中都学过

三：频繁项集和强规则

根据具体的场景，定义两个变量：

Minimum support 最小支持度 σ
Minimun confidence 最小置信度 Φ

所谓频繁项集大白话说就是这个项集出现的次数很频繁，界定方法：这个项集的支持度要大于最小支持度

所谓强规则大白话说就是这个规则很强大很有意义，界定方法：这个它置信度（条件概率）要大于最小置信度

3.1 什么是关联规则的挖掘？

给定 I ，D ，σ 和 Φ，然后我们去找出 X->Y之间的所有的强规则

用大白话说就是：当我有了所有的itemset ，dataset，最小支持度，最小置信度，然后去把X与Y之间，符合前面四个要要素的所有强规则都找出来，称为关联规则的挖掘

四. 从宏观的角度看如果进行关联规则挖掘

将所有的频繁项集都找出来，这也是最麻烦的一步
使用这些频繁项集，生成关联规则
- 遍历这个频繁项集，生成出他所有的非空子集
- 利用生成出来的所有的非空子集，将所有可能的关联规则都找出来
  - 找出来这些关联规则后去检验是否是强关联规则

可以看到, 哪怕仅仅存在4件商品, 他们之间的排列组合也是相当的多

五. Apriori算法

5.1 原理:

如果某个项集是频繁的, 那么它的所有非空子集也得是频繁的
如果某个项集是不频繁的, 那么它的所有超集也一定是不频繁的
所以, Apriori算法就是从单元素项集开始, 通过组合满足最小支持度的项集来形成更大的集合

5.2.0 例子: 找出所有的频繁项集

假设我们现在有如下的数据: 一共是9条记录, 我们规定这个场景下的支持度是3, 置信度是70%

transactions	itemset
1	{a, b, c, d}
2	{a, c, d, f}
3	{a, c, d, e, g}
4	{a, b, d, f}
5	{b, c, h}
6	{d, f, g}
7	{ a, b, g }
8	{c, d, f, g}
9	{b, c, d}

如果我们想找出频繁1项集, 也就是 L1的话, 很容易就能想到, 只要遍历所有的itemset中的每一个item ,然后记录下他们出现的次数, 但凡是出现次数大于3的, 都符合要求而被保留, 小于3的都不满足要求而被丢弃, 所以我们能得到下面的结果:

item	support
a	5
b	5
c	6
d	7
f	4
g	4

所以, 这个问题比较复杂的地方就是如何通过 lK -> CK+1 , 换句话说, 就是如何通过现在已知的 l1求出 C2

思路:

同样的我们可以对L1进行排列组合, 得出所有的情况称它为set1, 然后再遍历set1每一项, 去看看最开始给定的itemsets中是否包含它, 如果找到了包含它的项, 我们就给他的支持度计数+1, 同样的遍历完set1中所有的项后, 把支持度不满足的项删除, 保留支持度大于3的项, 至此, 也就意味着我们找到了 C2, 于是我们可以得到下面的结果

item	support
{a,b}	3
{a,c}	3
{a,d}	4
{b,c}	3
{b,d}	3
{c,d}	5
{d,f}	4
{d,g}	3

再往后就是从 L2 - > C3的过程:

思路1: 如果我们仍然使用自由组合的规则生成C3的话, 能产生向下先这么多的组合,实际上里面有很多不必要的项 根据Apriori算法的规定, 如果一个项集是不频繁的, 那么它的所有超集都是不频繁的

比如下面的{a,d,f} 其中的子项{a,d} 并不是频繁二项集, 那么我们根本没必要把它也组合进来, 因为一旦被组合进来之后, 就意味着我们要求去为他扫描数据库

item	support
{a,b,c}	1
{a,b,d}	2
{a,c,d}	3
{b,c,d}	2
{a,d,f}	X
{a,d,g}	X
{b,d,f}	X
{b,d,g}	X
{c,d,f}	X
{c,d,g}	X
{d,f,g}	X

那如果不自由组合, 具体怎么做呢?

第一步: 对所有的itemset进行一次排序, 因为第二步就要进行类似前缀的操作
第二步: 如果前k-1项相同, 第k项不同, 那么把第k项搬过去, 就得到新的候选项, 重复这个动作

通过步骤二的选择方式, 可以排除掉大量的肯定不频繁的候选项集, 但是也不能保证, 保存下来的候选项集就一定会是频繁的

所以, 如果我们遵循Apriori算法规定的话, 我们得到的集合如下应该长下面这样,

item	support
{a,b,c}	1
{a,b,d}	2
{a,c,d}	3
{b,c,d}	2

同样他们的支持度是具体是多少, 仍然得去扫描数据库, 实际上就是遍历这个C3, 然后看看一开始给定的itemsets中有多少个包含了它, 一旦发现就给它的计数+1 , 同样仅仅保存符合规则的, 得到如下的结果:

item	support
{a,c,d}	3

5.2.1 例子: 找出所有的强关联规则

找出所有的强关联规则, 大白话讲就是挨个计算所有的 L2 , L3 ... (频繁项集) 中, 他们的置信度是否在当前场景要求的70%以上, 如果满足了这个条件, 说明它就是强关联规则, (啤酒和尿布的关系)

计算公式就是它:

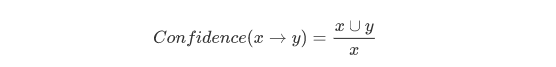
实际上就是计算：在Y发生的基础上， X发生的条件概率, 直接看公式就是 X和Y同时出现的次数 / X 出现的次数

举个例子：比如求a->b , 就是 a b同时发生的支持度/ a的支持度，前者中C2中可以查处来，后者从L1中可以查出来，也就是 3/5 = 60%

频繁2项集：

对于{a,b}
- a->b : 置信度为 3/5 = 60%
- b->a : 置信度为 3/5 = 60%
对于{a,c}
- a->c : 置信度为 3/5 = 60%
- c->a : 置信度为 3/6 = 50%
对于{a,d}
- a->d : 置信度为 4/5 = 80%
- d->a : 置信度为 3/7 = 57%
对于{b,c}
- b->c : 置信度为 3/5 = 60%
- c->b : 置信度为 3/6 = 50%
对于{b,d}
- b->d : 置信度为 3/5 = 60%
- d->b : 置信度为 3/7 = 42%
对于{c,d}
- c->d : 置信度为 5/6 = 83%
- d->c : 置信度为 5/7 = 71%
对于{d,f}
- d->f : 置信度为 4/7 = 57%
- f->d : 置信度为 4/4= 100%
对于{d,g}
- d->g : 置信度为 3/7 = 42%
- g->d : 置信度为 3/4 = 75%

如果规定置信度是70% ，那么强关联规则如下：

a->d
c->d
d->c
f->d
g->d

频繁3项集：

频繁3项集是 {a,c,d}，那么有如下几种情况

计算公式如上， {a,c,d}的置信度 / 箭头左边出现的项集的置信度

a,c -> d ：置信度是 3/3 = 100%
a,d -> c : 置信度是 3/4 = 75%
c,d -> a : 置信度是 3/5 = 60%
a -> c,d : 置信度是 3/5 = 60%
c -> a,d : 置信度是 3/6 = 50%
d -> a,c : 置信度是 3/7 = 42%

和标准的置信度比较，得到的结强关联规则如下：

a,c -> d
a,d -> c

5.3 代码实现:



# 加载数据集

def loadDataSet():

    return [

        ['a', 'b', 'c', 'd'],

        ['a', 'c', 'd', 'f'],

        ['a', 'c', 'd', 'e', 'g'],

        ['a', 'b', 'd', 'f'],

        ['b', 'c', 'h'],

        ['d', 'f', 'g'],

        ['a', 'b', 'g'],

        ['c', 'd', 'f', 'g'],

        ['b', 'c', 'd']]

# 选取数据集的非重复元素组成候选集的集合C1

def createC1(dataSet):

    C1 = []

    for transaction in dataSet:  # 对数据集中的每条购买记录

        for item in transaction:  # 对购买记录中的每个元素

            if [item] not in C1:  # 注意，item外要加上[]，便于与C1中的[item]对比

                C1.append([item])

    C1.sort()

    return list(map(frozenset, C1))  # 将C1各元素转换为frozenset格式，注意frozenset作用对象为可迭代对象

# 现在的CK是所有的一项集, 通过下面的前两个循环计算出每一个候选1项集出现的次数,进而才能判断出是否满足给定的支持度

# 由Ck产生Lk：扫描数据集D，计算候选集Ck各元素在D中的支持度，选取支持度大于设定值的元素进入Lk

def scanD(DataSet, Ck, minSupport):

    ssCnt = {}  # map字典结构, key = 项集 value = 支持度

    for tid in DataSet:  # 遍历每一条购买记录

        for can in Ck:  # 遍历Ck,也就是所有候选集

            if can.issubset(tid):  # 如果候选集包含在购买记录中，计数+1

                ssCnt[can] = ssCnt.get(can, 0) + 1

    numItems = float(len(DataSet))  # 购买记录数

    retList = []  # 用于存放支持度大于设定值的项集

    supportData = {}  # 用于记录各项集对应的支持度

    for key in ssCnt.keys():

        support = ssCnt[key] / numItems

        if support >= minSupport:

            retList.insert(0, key)  # 满足最小支持度就存储起来

        supportData[key] = support

    return retList, supportData  # 返回频繁1项集和他们各自的支持度

# 由Lk产生Ck+1 , 那第一次进来就是频繁1项集, 企图生成频繁二项集

def aprioriGen(Lk, k):  # Lk的k和参数k不是同一个概念，Lk表示频繁k项集,  参数K = CK+1 中的K+1

    retList = []

    lenLk = len(Lk)

    for i in range(lenLk):  # 分别遍历Lk中的每一项, 让它们和其他的项组合

        # 下面的for循环, 使用的是正宗的 类似前缀匹配的方式生成候选项集的方式

        for j in range(i + 1, lenLk):  # 从i+1开始, 是不让当前元素和自己也进行组合

            # 通过这两层循环, 就能实现类似这种组合 01, 02 ,03 ... 12,13,...

            L1 = list(Lk[i])[:k - 2]  # 将当前的频繁项集转换成list ,然后进行切片, 如果lk是频繁1项集, 这里根本切不出东西来

            L2 = list(Lk[j])[:k - 2]

            # 前缀匹配前肯定需要先排序,让它们相对是有序的

            L1.sort()

            L2.sort()

            if L1 == L2:  # 若前k-2项相同，则合并这两项

                retList.append(Lk[i] | Lk[j])  # 01, 02 ,03 ... 12,13,...

    return retList

# Apriori算法主函数

def apriori(dataSet, minSupport=0.5):

    # 创建c1

    C1 = createC1(dataSet)

    # todo 为啥需要去除重复?

    # 将dataset中所有的元素进行一次set去重, 然后转换成list返回得到D

    DataSet = list(map(set, dataSet))

    # 得到频繁1项集和各个项集的最小支持度

    L1, supportData = scanD(DataSet, C1, minSupport)

    L = [L1]

    k = 2

    # 从频繁1项集开始, 进行从Lk -> CK+1的生成

    while len(L[k - 2]) > 0:  # 当L[k]为空时，停止迭代

        Ck = aprioriGen(L[k - 2], k)  # L[k-2]对应的值是Lk-1

        # 获取到候选项集后, 重新扫描数据库, 计算出频繁项集,以及他们各自的支持度

        Lk, supK = scanD(DataSet, Ck, minSupport)

        # 更新他们各自的支持度

        supportData.update(supK)

        # 将新推导出来的频繁项集也添加进去

        L.append(Lk)

        k += 1

    return L, supportData

# 处理两个item项的 可信度（confidence）

def calcConf(freqSet, supportData, strong_rule, minConf):

    # 那么现在需要求出 frozenset([1]) -> frozenset([3]) 的可信度和 frozenset([3]) -> frozenset([1]) 的可信度

    for conseq in freqSet:

        # print 'confData=', freqSet, H, conseq, freqSet-conseq

        # 支持度定义: a -> b = support(a | b) / support(a).

        the_list = list(conseq)

        left = the_list[0]

        right = the_list[1]

        # 计算a-b

        conf = supportData[conseq] / supportData[frozenset({left})]

        if conf >= minConf:

            strong_rule.append("{} -> {}".format(frozenset({left}),frozenset({right})))

        # 计算b-a

        conf = supportData[conseq] / supportData[frozenset({right})]

        if conf >= minConf:

            strong_rule.append("{} -> {}".format(frozenset({right}), frozenset({left})))

def calcConfidence(Ck, fullSet,all_set,supportData, strong_rule, minConf):

    '''

        Ck  : k阶的频繁项集

        fullSet : k阶频繁项集拆开后的元素

        set : 由set 反向拆分出 Ck

        supportData,

        strong_rule,

        minConf

    '''

    for itemset in Ck:

        the_list = list(itemset)

        temp = fullSet.copy()

        for item in the_list:

           temp.remove({item})

        s = set()

        for i in temp:

            for j in i:

                s.add(j)

        # confidence(a->b) =  support(a,b) / support(a)

        confidence1 = supportData[all_set] / supportData[frozenset(itemset)]

        if(confidence1>=minConf):

            strong_rule.append("{} -> {}".format(frozenset(itemset), frozenset(s)))

        # confidence(b->a) =  support(a,b) / support(b)

        confidence2 = supportData[all_set] / supportData[frozenset(s)]

        if (confidence2 >= minConf):

            strong_rule.append("{} -> {}".format(frozenset(s), frozenset(itemset)))

def rulesFromConseq(freqSet, supportData, strong_rule, minConf):

    for itemset in freqSet:

        for set in itemset:

            H = list(set)

            the_list = []

            for i in H:

                the_list.append({i})

            LL = []

            LL.append(the_list)

            k = 2

            # 从频繁1项集开始, 进行从Lk -> CK+1的生成

            while len(LL[k - 2]) > 0:  # 当L[k]为空时，停止迭代

                # 直接对CK进行 统计置信度, 是因为根据Apriori算法的约定, 如果CK是频繁的,那么它的非空子集也是频繁的

                Ck = aprioriGen(LL[k - 2], k)  # L[k-2]对应的值是Lk-1

                # temp = the_list - Ck

                if len(Ck[0]) == len(the_list):

                    break

                else:

                    # 统计强关联规则

                    calcConfidence(Ck, LL[k - 2],set,supportData, strong_rule, minConf)

                    # 添加继续循环的条件

                    LL.append(Ck)

                    k += 1

def get_strong_rule(L,supportData,confidence):

    freSet = [L[k] for k in range(2, len(L))]

    strong_rule = []

    # 处理两项

    calcConf(L[1], supportData, strong_rule, confidence)

    # 处理三项及以上

    rulesFromConseq(freSet, supportData, strong_rule, confidence)

    return strong_rule

if __name__ == '__main__':

    minSupport = 0.3

    confidence = 0.7

    # 加载数据

    dataset = loadDataSet()

    # 找出各频繁项集, 及其支持度

    L, supportData = apriori(dataset, minSupport)

    # 找出强规则

    strong_rules = get_strong_rule(L, supportData,confidence)

    print('所有项集及其支持度: ',supportData)

    print('所有频繁项集: ',L)

    print("强规则:  ",strong_rules)

算法参考: 《机器学习实战》 Peter Harrington Chapter11

另外, 添加了求强规则的逻辑

六: Apriori算法的不足

每次虽然从Lk->CK+1 都是尽可能的生成出数量最少候选项集, 还保证了不会丢失频繁的候选项集, 但是依然需要校验生成出来的所有的候选项集的支持度是否符合场景要求的支持度大小, 不足的地方就体现在这里, 因为每次去校验的时候都得扫描一遍数据库, 如果数据库很大, 大量的IO会让算法变慢