图之强连通--Tarjan算法

强连通分量

简介

在阅读下列内容之前，请务必了解图论基础部分。

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图。

不懂再看看另一个版本的介绍

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。

如果有向图G的每两个顶点都强连通，称G是一个强连通图。

非强连通图有向图的极大强连通子图，称为强连通分量(SCC)。

这里想要介绍的是如何来求强连通分量。

Tarjan 算法

Robert E. Tarjan (1948~) 美国人。

Tarjan 发明了很多算法结构。光 Tarjan 算法就有很多，比如求各种联通分量的 Tarjan 算法，求 LCA（Lowest Common Ancestor，最近公共祖先）的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。

我们这里要介绍的是在有向图中求强连通分量的 Tarjan 算法。

另外，Tarjan 的名字 j 不发音，中文译为塔扬。

DFS 生成树

在介绍该算法之前，先来了解 DFS 生成树 ，我们以下面的有向图为例：

有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

1. 树边（tree edge）：绿色边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2. 反祖边（back edge）：黄色边，也被叫做回边，即指向祖先结点的边。
3. 横叉边（cross edge）：红色边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先时形成的。
4. 前向边（forward edge）：蓝色边，它是在搜索的时候遇到子树中的结点的时候形成的。

我们考虑 DFS 生成树与强连通分量之间的关系。

如果结点u是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以u为根的子树中。u被称为这个强连通分量的根。

反证法：假设有个结点v在该强连通分量中但是不在以u为根的子树中，那么u到v的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和u是第一个访问的结点矛盾了。得证。

Tarjan 算法求强连通分量（推荐）

在 Tarjan 算法中为每个结点u维护了以下几个变量：

1. DFN[u]：深度优先搜索遍历时结点 被搜索的次序。
2. LOW[u]：设以u为根的子树为Subtree(u) 。 LOW[u]定义为以下结点的 的最小值:Subtree(u)中的结点；从Subtree(u)通过一条不在搜索树上的边能到达的结点。

一个结点的子树内结点的 DFN 都大于该结点的 DFN。

从根开始的一条路径上的 DFN 严格递增，LOW 严格非降。

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索。在搜索过程中，对于结点 和与其相邻的结点 （v 不是 u 的父节点）考虑 3 种情况：

1. v未被访问：继续对v进行深度搜索。在回溯过程中，用LOW[v]更新LOW[u]。因为存在从u到v的直接路径，所以v能够回溯到的已经在栈中的结点，u也一定能够回溯到。
2. v被访问过，已经在栈中：即已经被访问过，根据LOW值的定义（能够回溯到的最早的已经在栈中的结点），则用DFN[v]更新LOW[u]。
3. v被访问过，已不在在栈中：说明v已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

下面更有助于理解,要好好看看：

做一遍DFS，用dfn[i]表示编号为i的节点在DFS过程中 的访问序号(也可以叫做开始时间）。

在DFS过程中会形成 一搜索树。在搜索树上越先遍历到的节点，显然DFN的值就越小。DFN值越小的节点，就称为越“早” 。

用low[i]表示从i节点出发DFS过程中i下方节点(开始时间大 于DFN[i]，且由i可达的节点）所能到达的最早的节点的开始时间。初始时LOW[i]=DFN[i]

DFS过程中，碰到哪个节点，就将哪个节点入栈。栈中节点只有在其所属的强连通分量已经全部求出时，才会出栈。

如果发现某节点u有边连到栈里的节点v，则更新u的LOW值 为min(LOW[u],DFN[v]) ，若LOW[u]被更新为DFN[v],则表明目前 发现u可达的最早的节点是v.

对于u的子节点v，从v出发进行的DFS结束回到u时，使得 LOW[u] = min(LOW[u],LOW[v])。因为u可达v, 所以v可达的最早的节点，也是u可达的。

如果一个节点u，从其出发进行的DFS已经全部完成并回到u，而且此时其LOW值等于DFN值，则说明u可达的所有节点，都不能到达任何比u早的节点 --- 那么该节点u就是一个强连通分量在DFS搜索树中的根。

此时，显然栈中u上方的节点，都是不能到达比u早的节点的。将栈中节点弹出，一直弹到u(包括u), 弹出的节点就构成了一个强连通分量.

将上述算法写成伪代码：

 TARJAN_SEARCH(int u)
     vis[u]=true
     low[u]=dfn[u]=++dfncnt
     push u to the stack
     for each (u,v) then do
         if v hasn't been search then
             TARJAN_SEARCH(v) // 搜索
             low[u]=min(low[u],low[v])// 回溯
         else if v has been in the stack then
             low[u]=min(low[u],dfn[v])

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个DFN[u]=LOW[u] 。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 DFN 值和 LOW 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定DFN[u]=LOW[u]的条件是否成立，如果成立，则栈中从u后面的结点构成一个 SCC。

实现

 int dfn[N], low[N], dfncnt, s[N], tp;
 int scc[N], sc;  // 结点 i 所在 scc 的编号
 int sz[N];       // 强连通 i 的大小
 void tarjan(int u) {
   low[u] = dfn[u] = ++dfncnt, s[++tp] = u;
   for (int i = h[u]; i; i = e[i].nex) {
     const int &v = e[i].t;
     if (!dfn[v])
       tarjan(v), low[u] = min(low[u], low[v]);
     else if (!scc[v])
       low[u] = min(low[u], dfn[v]);
   }
   if (dfn[u] == low[u]) {
     ++sc;
     while (s[tp] != u) scc[s[tp]] = sc, sz[sc]++, --tp;
     scc[s[tp]] = sc, sz[sc]++, --tp;
   }
 }

时间复杂度O(n+m) 。

Kosaraju 算法（直接粘别人的，我也没怎么看：)   ，不是很懂）

Kosaraju 算法依靠两次简单的 DFS 实现。

第一次 DFS，选取任意顶点作为起点，遍历所有为访问过的顶点，并在回溯之前给顶点编号，也就是后序遍历。

第二次 DFS，对于反向后的图，以标号最大的顶点作为起点开始 DFS。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的结点，选取标号最大的，重复上述过程。

两次 DFS 结束后，强连通分量就找出来了，Kosaraju 算法的时间复杂度为O(n+m)。

实现

 // g 是原图，g2 是反图

 void dfs1(int u) {
   vis[u] = true;
   for (int v : g[u])
     if (!vis[v]) dfs1(v);
   s.push_back(v);
 }

 void dfs2(int u) {
   color[u] = sccCnt;
   for (int v : g2[u])
     if (!color[v]) dfs2(v);
 }

 void kosaraju() {
   sccCnt = ;
   for (int i = ; i <= n; ++i)
     if (!vis[i]) dfs1(i);
   for (int i = n; i >= ; --i)
     if (!color[s[i]]) {
       ++sccCnt;
       dfs2(s[i])
     }
 }

Garbow 算法（不写了，也用不上，感兴趣的自己去了解一下吧）

接下来我们讨论一下Tarjan算法能够干一些什么：

既然我们知道，Tarjan算法相当于在一个有向图中找有向环，那么我们Tarjan算法最直接的能力就是缩点辣！

缩点基于一种染色实现，我们在DFS的过程中，尝试把属于同一个强连通分量的点都染成一个颜色，那么同一个颜色的点，就相当于一个点。

将一个有向带环图变成了一个有向无环图(DAG图)。很多算法要基于有向无环图才能进行的算法就需要使用Tarjan算法实现染色缩点，如拓扑排序等，建一个DAG图然后再进行算法处理。

在这种场合，Tarjan算法就有了很大的用武之地辣！

举个简单的例子，求一条路径，可以经过重复结点，要求经过的不同结点数量最多。

推荐题目

USACO Fall/HAOI 2006 受欢迎的牛

POJ1236 Network of Schools

---

下面转载一篇特别易懂的关于Tarjan算法的博客

原文：https://blog.csdn.net/justlovetao/article/details/6673602

直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法，两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。 [Tarjan算法]

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出，

 Low(u)=Min
 {
    DFN(u),
    Low(v),(u,v)为树枝边，u为v的父节点
    DFN(v),(u,v)为指向栈中节点的后向边(非横叉边)
 }

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

算法伪代码如下

 tarjan(u)
 {
     DFN[u]=Low[u]=++Index                      // 为节点u设定次序编号和Low初值
     Stack.push(u)                              // 将节点u压入栈中
     for each (u, v) in E                       // 枚举每一条边
         if (v is not visted)               // 如果节点v未被访问过
             tarjan(v)                  // 继续向下找
             Low[u] = min(Low[u], Low[v])
         else if (v in S)                   // 如果节点v还在栈内
             Low[u] = min(Low[u], DFN[v])
     if (DFN[u] == Low[u])                      // 如果节点u是强连通分量的根
         repeat
             v = S.pop                  // 将v退栈，为该强连通分量中一个顶点
             print v
         until (u== v)
 }

接下来是对算法流程的演示。（重要，建议自己也在草稿纸上跟着模拟一下）

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

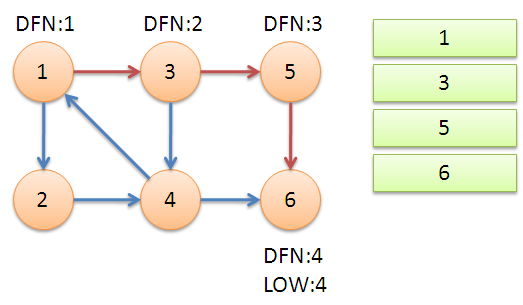
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

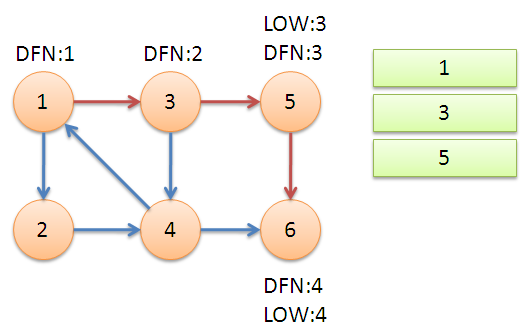
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

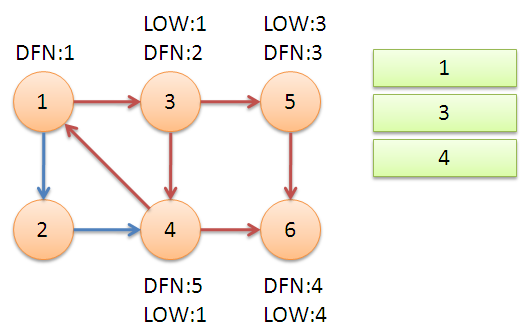
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

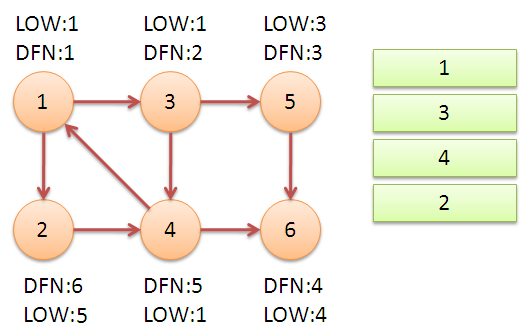
可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

求有向图的强连通分量还有一个强有力的算法，为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是 O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外，该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法，也有助于深入理解求双连通分量的Tarjan算法，两者可以类比、组合理解。

求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法，以及求最近公共祖先的离线Tarjan算法，在此对Tarjan表示崇高的敬意。

附：Tarjan算法的C++程序

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 #define N 100
 #define M 100
 struct Edge
 {
     int v;
     int next;
 };
 Edge edge[M];//边的集合

 int node[N];//顶点集合
 int instack[N];//标记是否在stack中
 int stack[N];
 int Belong[N];//各顶点属于哪个强连通分量
 int DFN[N];//节点u搜索的序号(时间戳)
 int LOW[N];//u或u的子树能够追溯到的最早的栈中节点的序号(时间戳)
 int n, m;//n：点的个数；m：边的条数
 int cnt_edge;//边的计数器
 int Index;//序号(时间戳)
 int top;
 int Bcnt;//有多少个强连通分量

 void add_edge(int u, int v)//邻接表存储
 {
     edge[cnt_edge].next = node[u];
     edge[cnt_edge].v = v;
     node[u] = cnt_edge++;
 }
 void tarjan(int u)
 {
     int i,j;
     int v;
     DFN[u]=LOW[u]=++Index;
     instack[u]=true;
     stack[++top]=u;
     for (i = node[u]; i != -; i = edge[i].next)
     {
         v=edge[i].v;
         if (!DFN[v])//如果点v没被访问
         {
             tarjan(v);
             if (LOW[v]<LOW[u])
                 LOW[u]=LOW[v];
         }
         else//如果点v已经被访问过
             if (instack[v] && DFN[v]<LOW[u])
                 LOW[u]=DFN[v];
     }
     if (DFN[u]==LOW[u])
     {
         Bcnt++;
         do
         {
             j=stack[top--];
             instack[j]=false;
             Belong[j]=Bcnt;
         }
         while (j!=u);
     }
 }
 void solve()
 {
     int i;
     top=Bcnt=Index=;
     memset(DFN,,sizeof(DFN));
     memset(LOW,,sizeof(LOW));
     for (i=;i<=n;i++)
         if (!DFN[i])
             tarjan(i);
 }
 int main()
 {
     freopen("in.txt","r",stdin);
     int i,j,k;
     cnt_edge=;
     memset(node,-,sizeof(node));
     scanf("%d%d",&n,&m);
     for(i=;i<=m;i++)
     {
         scanf("%d%d",&j,&k);
         add_edge(j,k);
     }
     solve();
     for(i=;i<=n;i++)
         printf("%d ",Belong[i]);
 }
  

我自己根据模板写的适合我用的（可以忽略）

 #include <stdio.h>
 #include <string.h>
 #include <algorithm>
 #include <stack>
 using namespace std;
 #define N 100
 #define M 100

 struct Edge{
     int v;
     int next;
 }Edge[M];//边的集合

 int node[N];//顶点集合
 int instack[N];//标记是否在stack中
 int Belong[N];//各顶点属于哪个强连通分量
 int DFN[N];//节点u搜索的序号(时间戳)
 int LOW[N];//u或u的子树能够追溯到的最早的栈中节点的序号(时间戳)
 int n,m;//n：点的个数；m：边的条数
 int cnt_edge;//边的计数器
 int Index;//序号(时间戳)
 int Bcnt; //有多少个强连通分量
 stack<int> sk;

 void add_edge(int u,int v)//邻接表存储
 {
     Edge[cnt_edge].next=node[u];
     Edge[cnt_edge].v=v;
     node[u]=cnt_edge++;
 }

 void tarjan(int u)
 {
     DFN[u]=LOW[u]=++Index;
     instack[u]=;
     sk.push(u);
     for(int i=node[u];i!=-;i=Edge[i].next)
     {
         int v=Edge[i].v;
         if(!DFN[v])//如果点v没被访问
         {
             tarjan(v);
             LOW[u]=min(LOW[u],LOW[v]);
         }
         else //如果点v已经被访问过
         {
             if(instack[v]&&DFN[v]<LOW[u])
                 LOW[u]=DFN[v];
         }
     }
     if(DFN[u]==LOW[u])
     {
         Bcnt++;
         int t;
         do{
             t=sk.top();
             sk.pop();
             instack[t]=;
             Belong[t]=Bcnt;
         }while(t!=u);
     }
 }

 int main()
 {
     freopen("sample.txt","r",stdin);
     memset(node,-,sizeof(node));
     scanf("%d %d",&n,&m);
     for(int i=;i<=m;i++)
     {
         int a,b;
         scanf("%d %d",&a,&b);
         add_edge(a,b);
     }
     for(int i=;i<=n;i++)
     {
         if(!DFN[i])
         {
             tarjan(i);
         }
     }
     for(int i=;i<=n;i++)
     {
         printf("%d ",Belong[i]);
     }
     return  ;
 }

---

下面给出两道例题，可以试着做做，可以加深理解哦

POJ-2186 Popular Cows

http://poj.org/problem?id=2186

Description

Every cow's dream is to become the most popular cow in the herd. In a herd of N (1 <= N <= 10,000) cows, you are given up to M (1 <= M <= 50,000) ordered pairs of the form (A, B) that tell you that cow A thinks that cow B is popular. Since popularity is transitive, if A thinks B is popular and B thinks C is popular, then A will also think that C is 
popular, even if this is not explicitly specified by an ordered pair in the input. Your task is to compute the number of cows that are considered popular by every other cow. 

Input

* Line 1: Two space-separated integers, N and M 
* Lines 2..1+M: Two space-separated numbers A and B, meaning that A thinks B is popular. 

Output

* Line 1: A single integer that is the number of cows who are considered popular by every other cow. 

Sample Input

Sample Output

Hint

Cow 3 is the only cow of high popularity. 

题意：

给定一个有向图，求有多少个顶点是由任何顶点出发都可达的。 
有向无环图中唯一出度为0的点，一定可 以由任何点出发均可达(由于无环，所以从任何点出发往前走，必然终止于 一个出度为0的点) 
解题思路 ：
1. 求出所有强连通分量 
2. 每个强连通分量缩成一点，则形成一个有 向无环图DAG。 
3. DAG上面如果有唯一的出度为0的点,则该点 能被所有的点可达。那么该点所代表的连通分 量上的所有的原图中的点，都能被原图中的所 有点可达，则该连通分量的点数，就是答案。 
4. DAG上面如果有不止一个出度为0的点，则 这些点互相不可达，原问题无解，答案为0

缩点的时候不一定要构造新图，只要把不同强连通分量的点染不同颜色，然后考察各种颜色的点有没有连到别的颜色的边即可(即其对应的缩点后的DAG图上的点是否有出边）。

代码：

不贴了，和下一题差不多

---

Network of Schools

http://poj.org/problem?id=1236

Description

A number of schools are connected to a computer network. Agreements have been developed among those schools: each school maintains a list of schools to which it distributes software (the “receiving schools”). Note that if B is in the distribution list of school A, then A does not necessarily appear in the list of school B 
You are to write a program that computes the minimal number of schools that must receive a copy of the new software in order for the software to reach all schools in the network according to the agreement (Subtask A). As a further task, we want to ensure that by sending the copy of new software to an arbitrary school, this software will reach all schools in the network. To achieve this goal we may have to extend the lists of receivers by new members. Compute the minimal number of extensions that have to be made so that whatever school we send the new software to, it will reach all other schools (Subtask B). One extension means introducing one new member into the list of receivers of one school. 

Input

The first line contains an integer N: the number of schools in the network (2 <= N <= 100). The schools are identified by the first N positive integers. Each of the next N lines describes a list of receivers. The line i+1 contains the identifiers of the receivers of school i. Each list ends with a 0. An empty list contains a 0 alone in the line.

Output

Your program should write two lines to the standard output. The first line should contain one positive integer: the solution of subtask A. The second line should contain the solution of subtask B.

Sample Input

Sample Output

题目大意：

给定一个有向图，求：

1. 至少要选几个顶点，才能做到从这些顶点出发，可以到达全部顶点
2. 至少要加多少条边，才能使得从任何一个顶点出发，都能到达全部顶点

有用的定理:

　　　　有向无环图中所有入度不为0的点，一定可以由某个入度为0的点出发可达。 (由于无环，所以从任何入度不为0的点往回走，必然终止于一个入度为0的点)

解题思路 :

我们可以先进行缩点求出dag图，然后我们考虑第一个问题，求最少发几套软件可以全覆盖，首先题意已经保证了是联通的。然后我们可以想，如果我们把所有没有入边的点都放上软件，是一定可行的。有入边的一定会通过一些边最终从一定有出边的发放软件的地方获得软件。

然后我们考虑第二个问题。这是一个连通图。如果我们有些点没有入点，有些点没出点。那我们如果想办法将入点和一些出点相连，就能保证最后会成为很多圆相连。这样子答案就是没有入边的点和没有出边的点的最大值。

具体来说：

1. 求出所有强连通分量
2. 每个强连通分量缩成一点，则形成一个有向无环图DAG。
3. DAG上面有多少个入度为0的顶点，问题1的答案就是多少

在DAG上要加几条边，才能使得DAG变成强连通的，问题2的答案就是多少

加边的方法： 要为每个入度为0的点添加入边，为每个出度为0的点添加出边 ，假定有 n 个入度为0的点，m个出度为0的点， max(m,n)就是第二个问题的解(证明难，略）

 代码如下：

 #include <stdio.h>
 #include <iostream>
 #include <string.h>
 #include <algorithm>
 #include <stack>
 #include <string>
 #include <sstream>
 using namespace std;
 #define maxn 105

 struct Edge{
     int v;
     int next;
 }Edge[maxn*maxn];//边的集合,边最多为n*(n-1),故要开点数的平方

 int node[maxn];//顶点集合
 int instack[maxn];//标记是否在stack中
 int Belong[maxn];//各顶点属于哪个强连通分量
 int DFN[maxn];//节点u搜索的序号(时间戳)
 int LOW[maxn];//u或u的子树能够追溯到的最早的栈中节点的序号(时间戳)
 int n;//n：点的个数
 int cnt_edge;//边的计数器
 int Index;//序号(时间戳)
 int Bcnt; //有多少个强连通分量
 int out[maxn];//存储出度
 int in[maxn];//存储入度
 stack<int> sk;

 void add_edge(int u,int v)//邻接表存储
 {
     Edge[cnt_edge].next=node[u];
     Edge[cnt_edge].v=v;
     node[u]=cnt_edge++;
 }

 void tarjan(int u)
 {
     DFN[u]=LOW[u]=++Index;
     instack[u]=;
     sk.push(u);
     for(int i=node[u];i!=-;i=Edge[i].next)
     {
         int v=Edge[i].v;
         if(!DFN[v])//如果点v没被访问
         {
             tarjan(v);
             LOW[u]=min(LOW[u],LOW[v]);
         }
         else //如果点v已经被访问过
         {
             if(instack[v])
                 LOW[u]=min(LOW[u],DFN[v]);
         }
     }
     if(DFN[u]==LOW[u])
     {
         Bcnt++;
         int t;
         do{
             t=sk.top();
             sk.pop();
             instack[t]=;
             Belong[t]=Bcnt;
         }while(t!=u);
     }
 }

 void work()
 {
     for(int i=;i<=n;i++)
     {
         for(int j=node[i];j!=-;j=Edge[j].next)
         {
             int v=Edge[j].v;
             if(Belong[i]!=Belong[v])
             {
                 out[Belong[i]]++;
                 in[Belong[v]]++;
             }
         }
     }
     int RU=;
     int CHU=;
     for(int i=;i<=Bcnt;i++)
     {
         if(!in[i]) RU++;
         if(!out[i]) CHU++;
     }
     if(Bcnt==)
         printf("1\n0\n");
     else
         printf("%d\n%d\n",RU,max(RU,CHU));
 }

 int main()
 {
     //freopen("sample.txt","r",stdin);
     memset(node,-,sizeof(node));
     scanf("%d",&n);
     getchar();
     for(int i=;i<=n;i++)
     {
         int v;
         string str;
         getline(cin,str);
         istringstream ss(str);
         while(ss >> v&&v)
         {
             add_edge(i,v);
         }
     }
     for(int i=;i<=n;i++)
     {
         if(!DFN[i])
         {
             tarjan(i);
         }
     }
     work();
     return  ;
 }

---