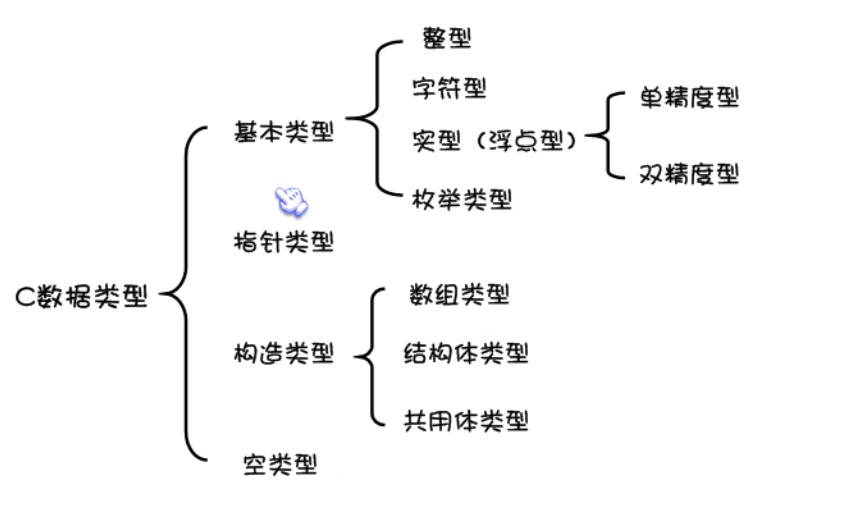
C语言数据类型整理

基本类型：
　　它们是算术类型，包括两种类型：整数类型和浮点类型。

枚举类型：
　　它们也是算术类型，被用来定义在程序中只能赋予其一定的离散整数值的变量。

void 类型：
　　类型说明符 void 表明没有可用的值。

派生类型：
　　它们包括：指针类型、数组类型、结构类型、共用体类型和函数类型。

signed 指示被声明的对象的类型为有符号的类型。

unsigned 指示被声明的对象的类型为无符号类型。

无符号（unsigned）和有符号（signed）两种类型（float和double总是带符号的），在除char以外的数据类型中，声明的整型变量都是有符号的类型；char在默认情况下总是无符号的。

有符号整数类型

类型名称	字节数	取值范围
signed char	1	-2^7 ~ 2^7-1
short int 或 short	2	-2^15 ~ 2^15-1
int	4	-2^31 ~ 2^31-1
long int 或 long	4	-2^31 ~ 2^31-1
long long int 或 long long	8	-2^63 ~ 2^63-1

  　　　　　　　　    　　　　
    　　　　　　 　　    　　　　
   　　　　　　    　　 　　
 　　　　　　　　　　 　　    　　 　　
   　　　　    　　  　　 　　
     　　   　　　　

无符号整数类型
类型名称     　　　　　　　　　　　　　　　　　　字节数     　　　　　　取值范围
unsigned char     　　　　　　　　　　　　　　　　　 1    　　　　　　　　0 ~ 2^8
unsigned short int 或 unsigned short    　　　 　　　　  2    　　　　　　　    0 ~ 2^16
unsigned int     　　　　　　　　　　　　　　　　　　 4     　　　　　　　   0 ~ 2^32
unsigned long int 或 unsigned long     　　　　　　　　 4    　　　　　　　　 0 ~ 2^32
unsigned long long int 或 unsigned long long     　　　　8    　　　　　　　　 0 ~ 2^64

浮点类型

类型名称	字节数	取值范围
float	4	-/+3.4e38（精确到6位小数）
double	8	-/+1.7e308（精确到15位小数）
long double	12	-/+1.19e4932（精确到18位小数）

极限值符号
表示有符号整数类型的极限值符号
类型名称     　　　　下限     　　　　　　　上限
char     　　　　　　 CHAR_MIN    　　　　 CHAR_MAX
short     　　　　　　SHRT_MIN    　　　　 SHRT_MAX
int     　　　　　　　INT_MIN    　　　　　　INT_MAX
long     　　　　　　LONG_MIN    　　　　 LONG_MAX
long long     　　　　LLONG_MIN     　　　　LLONG_MAX

表示无符号整数类型的极限值符号
类型名称     　　　　　　 下限     　　　　　　上限
unsigned char     　　　　 0     　　　　　　UCHAR_MAX
unsigned short    　　　　 0    　　　　　　 USHRT_MAX
unsigned int     　　　　　 0     　　　　　　　UINT_MAX
unsigned long     　　　　 0     　　　　　　ULONG_MAX
unsigned long long     　　0     　　　　　　ULLONG_MAX

表示浮点类型的极限值符号

类型名称	下限	上限
float	FLT_MIN	FLT_MAX
double	DBL_MIN	DBL_MAX
long double	LDBL_MIN	LDBL_MAX