OpenCV-Python 轮廓特征

目标

在本文中，我们将学习

如何找到轮廓的不同特征，例如面积，周长，质心，边界框等。
您将看到大量与轮廓有关的功能。

1. 特征矩

特征矩可以帮助您计算一些特征，例如物体的质心，物体的面积等。请查看特征矩上的维基百科页面。函数cv.moments()提供了所有计算出的矩值的字典。见下文：

import numpy as np
import cv2 as cv
img = cv.imread('star.jpg',0)
ret,thresh = cv.threshold(img,127,255,0)
contours,hierarchy = cv.findContours(thresh, 1, 2)
cnt = contours[0]
M = cv.moments(cnt)
print( M )

从这一刻起，您可以提取有用的数据，例如面积，质心等。质心由关系给出，Cx=M10M00C_x = \frac{M_{10}}{M_{00}}Cx=M00M10 和 Cy=M01M00C_y = \frac{M_{01}}{M_{00}}Cy=M00M01。可以按照以下步骤进行：

cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])

2. 轮廓面积

轮廓区域由函数cv.contourArea()或从矩M['m00']中给出。

area = cv.contourArea(cnt)

3. 轮廓周长

也称为弧长。可以使用cv.arcLength()函数找到它。第二个参数指定形状是闭合轮廓(True)还是曲线。

perimeter = cv.arcLength(cnt,True)

4. 轮廓近似

根据我们指定的精度，它可以将轮廓形状近似为顶点数量较少的其他形状。它是Douglas-Peucker算法的实现。检查维基百科页面上的算法和演示。

为了理解这一点，假设您试图在图像中找到一个正方形，但是由于图像中的某些问题，您没有得到一个完美的正方形，而是一个“坏形状”（如下图所示）。现在，您可以使用此功能来近似形状。在这种情况下，第二个参数称为epsilon，它是从轮廓到近似轮廓的最大距离。它是一个精度参数。需要正确选择epsilon才能获得正确的输出。

epsilon = 0.1*cv.arcLength(cnt,True)
approx = cv.approxPolyDP(cnt,epsilon,True)

下面，在第二张图片中，绿线显示了ε=弧长的10％时的近似曲线。第三幅图显示了ε=弧长度的1％时的情况。第三个参数指定曲线是否闭合。

5. 轮廓凸包

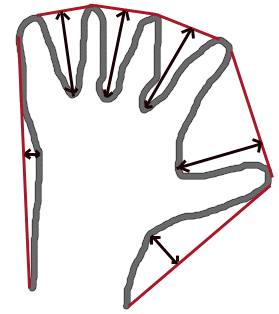
凸包外观看起来与轮廓逼近相似，但不相似（在某些情况下两者可能提供相同的结果）。在这里，cv.convexHull()函数检查曲线是否存在凸凹缺陷并对其进行校正。一般而言，凸曲线是始终凸出或至少平坦的曲线。如果在内部凸出，则称为凸度缺陷。例如，检查下面的手的图像。红线显示手的凸包。双向箭头标记显示凸度缺陷，这是凸包与轮廓线之间的局部最大偏差。

关于它的语法，有一些需要讨论：

hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]

参数详细信息：

点是我们传递到的轮廓。
凸包是输出，通常我们忽略它。
顺时针方向：方向标记。如果为True，则输出凸包为顺时针方向。否则，其方向为逆时针方向。
returnPoints：默认情况下为True。然后返回凸包的坐标。如果为False，则返回与凸包点相对应的轮廓点的索引。

因此，要获得如上图所示的凸包，以下内容就足够了：

hull = cv.convexHull(cnt)

但是，如果要查找凸度缺陷，则需要传递returnPoints = False。为了理解它，我们将拍摄上面的矩形图像。首先，我发现它的轮廓为cnt。现在，我发现它的带有returnPoints = True的凸包，得到以下值：[[[234 202]]，[[51 202]]，[[51 79]]，[[234 79]]]，它们是四个角矩形的点。现在，如果对returnPoints = False执行相同的操作，则会得到以下结果：[[129]，[67]，[0]，[142]]。这些是轮廓中相应点的索引。例如，检查第一个值：cnt [129] = [[234，202]]与第一个结果相同（对于其他结果依此类推）。

当我们讨论凸度缺陷时，您将再次看到它。

6. 检查凸度

cv.isContourConvex()具有检查曲线是否凸出的功能。它只是返回True还是False。没什么大不了的。

k = cv.isContourConvex(cnt)

7. 边界矩形

有两种类型的边界矩形。

7.a.直角矩形

它是一个矩形，不考虑物体的旋转。所以边界矩形的面积不是最小的。它是由函数cv.boundingRect()找到的。

令(x，y)为矩形的左上角坐标，而(w，h)为矩形的宽度和高度。

x,y,w,h = cv.boundingRect(cnt)
cv.rectangle(img,(x,y),(x w,y h),(0,255,0),2)

7.b. 旋转矩形

这里，边界矩形是用最小面积绘制的，所以它也考虑了旋转。使用的函数是cv.minAreaRect()。它返回一个Box2D结构，其中包含以下细节 -(中心(x,y)，(宽度，高度)，旋转角度)。但要画出这个矩形，我们需要矩形的四个角。它由函数cv.boxPoints()获得

rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img,[box],0,(0,0,255),2)

两个矩形都显示在一张单独的图像中。绿色矩形显示正常的边界矩形。红色矩形是旋转后的矩形。

8. 最小闭合圈

接下来，使用函数**cv.minEnclosingCircle(*()查找对象的圆周。它是一个以最小面积完全覆盖物体的圆。

(x,y),radius = cv.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
cv.circle(img,center,radius,(0,255,0),2)

9. 拟合一个椭圆

下一个是把一个椭圆拟合到一个物体上。它返回内接椭圆的旋转矩形。

ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),2)

10. 拟合直线

同样，我们可以将一条直线拟合到一组点。下图包含一组白点。我们可以近似一条直线。

rows,cols = img.shape[:2]
[vx,vy,x,y] = cv.fitLine(cnt, cv.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx)   y)
righty = int(((cols-x)*vy/vx) y)
cv.line(img,(cols-1,righty),(0,lefty),(0,255,0),2)

欢迎关注磐创博客资源汇总站：

http://docs.panchuang.net/

欢迎关注PyTorch官方中文教程站：

http://pytorch.panchuang.net/

OpenCV中文官方文档：

http://woshicver.com/