SPOJ QTREE4 - Query on a tree IV 树分治

题意：

给出一棵边带权的树，初始树上所有节点都是白色。

有两种操作：

• C x，改变节点x的颜色，即白变黑，黑变白
• A，询问树中最远的两个白色节点的距离，这两个白色节点可以重合(此时距离为0)。

分析：

网上大概有3中解法，树链剖分，点分支，边分治。

这里用的是漆子超论文中边分治的解法。

重构树形态

因为边分治遇到菊花形的树复杂度会退化，所以我们要重构一遍树。



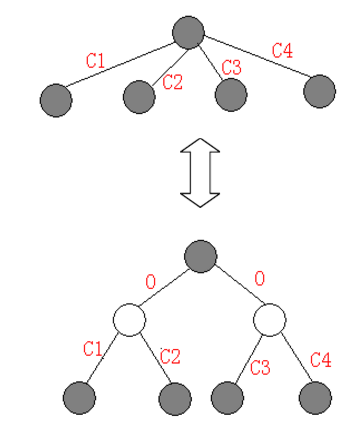
向树中加入一些虚点，连接到虚点的边的权值都为0，而且将虚点的颜色设为黑色。

这样就得到一棵二叉树，而且不会影响正确答案。

重构以后的树的顶点个数会变成原来的两倍左右。

分治过程

分治的时候我们首先要找到树的中心边，即两端较大子树最小的那条边。

相距最远的两个白点，有两种情况：

1. 都在中心边的某侧子树中，这种情况我们递归处理。
2. 最长路径经过中心边，也就是两点分别在两个子树中。

对于第二种情况，我们维护两个优先队列，子树中的白点到根节点的最远距离。

这样我们便能很快求得经过中心边的最长路径。

另外，我们不能确定最远路径经过哪棵子树的中心边，所以还要维护一个整体的堆，即经过各个子树中心边能得到的最长路径。

修改操作

预处理的时候，顺便记录下来每个节点分别都在哪些子树中。

这样修改点的颜色后，不光要修改对应优先队列的内容，还要手工维护那个全局的堆。

因为一个点最多被O(logn)棵树包含，修改每棵树的复杂度是O(logn)，所以每次修改的复杂度为O(log^2n)。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
#define F first
#define S second
#define MP make_pair
using namespace std;

typedef pair<int, int> PII;
const int maxn = 200000 + 10;
const int INF = 0x3f3f3f3f;

struct Edge
{
	int v, w, nxt;
	Edge() {}
	Edge(int v, int w, int nxt): v(v), w(w), nxt(nxt) {}
};

int n, m, color[maxn];

int head[maxn], tmp[maxn], ecnt;
Edge edges[maxn * 4];

void build(vector<int>& ch, int u, int L, int R) {
	if(L > R) return;
	if(L == R) {
		Edge& e = edges[ch[L]];
		int v = e.v, w = e.w;
		//printf("AddEdge %d <---> %d\n", u, v);
		edges[ecnt] = Edge(v, w, tmp[u]); tmp[u] = ecnt++;
		edges[ecnt] = Edge(u, w, tmp[v]); tmp[v] = ecnt++;
		return;
	}

	int M = (L + R) / 2;
	int o = ++n; color[o] = 1;
	//printf("AddEdge %d <---> %d\n", u, o);
	edges[ecnt] = Edge(o, 0, tmp[u]); tmp[u] = ecnt++;
	edges[ecnt] = Edge(u, 0, tmp[o]); tmp[o] = ecnt++;
	build(ch, o, L, M);
	build(ch, o, M+1, R);
}

void rebuild(int u, int fa) {
	vector<int> ch;
	for(int i = head[u]; ~i; i = edges[i].nxt) {
		int v = edges[i].v;
		if(v == fa) continue;
		rebuild(v, u);
		ch.push_back(i);
	}
	if(!ch.empty()) {
		int sz = ch.size() - 1;
		int mid = sz / 2;
		build(ch, u, 0, mid);
		build(ch, u, mid + 1, sz);
	}
}

bool del[maxn];
int sz[maxn], tot, pos[maxn];
priority_queue<PII> PQ[maxn * 2];
vector<PII> b[maxn];
PII heap[maxn];
char op[5];

PII findCenter(int u, int fa, int cnt) {
	sz[u] = 1;
	PII ans(INF, -1);
	int m = 0;
	for(int i = head[u]; ~i; i = edges[i].nxt) {
		int v = edges[i].v;
		if(del[i >> 1] || v == fa) continue;
		ans = min(ans, findCenter(v, u, cnt));
		sz[u] += sz[v];
		ans = min(ans, MP(max(sz[v], cnt - sz[v]), i));
	}
	return ans;
}

void getdist(int u, int fa, int d, int id) {
	b[u].push_back(MP(id, d));
	if(!color[u]) PQ[id].push(MP(d, u));
	++tot;
	for(int i = head[u]; ~i; i = edges[i].nxt) {
		Edge& e = edges[i];
		int v = e.v, w = e.w;
		if(del[i >> 1] || v == fa) continue;
		getdist(v, u, d + w, id);
	}
}

void divide(int u, int cnt) {
	if(cnt <= 1) return;
	int s = findCenter(u, 0, cnt).S;
	del[s >> 1] = true;

	tot = 0; PQ[s].push(MP(-INF, -1));
	getdist(edges[s].v, 0, 0, s);
	int sz1 = tot;
	tot = 0; PQ[s^1].push(MP(-INF, -1));
	getdist(edges[s^1].v, 0, 0, s^1);
	int sz2 = tot;

	heap[s >> 1] = MP(PQ[s].top().F + edges[s].w + PQ[s^1].top().F, s >> 1);

	divide(edges[s].v, sz1);
	divide(edges[s^1].v, sz2);
}

void down(int x) {
    int i = x , j = i << 1 | 1;
    pair<int , int> t = heap[i];
    if (j + 1 < m && heap[j + 1] > heap[j])
        ++ j;
    while (j < m && t < heap[j]) {
        pos[heap[j].second] = i , heap[i] = heap[j];
        i = j , j = i << 1 | 1;
        if (j + 1 < m && heap[j + 1] > heap[j])
            ++ j;
    }
    heap[i] = t , pos[t.second] = i;
}

void up(int x) {
    int i = x , j = (i + 1 >> 1) - 1;
    pair<int , int> t = heap[i];
    while (j >= 0 && heap[j] < t) {
        pos[heap[j].second] = i , heap[i] = heap[j];
        i = j , j = (i + 1 >> 1) - 1;
    }
    heap[i] = t , pos[t.second] = i;
}

int main()
{
	scanf("%d", &n);
	memset(head, -1, sizeof(head));
	ecnt = n * 6;
	for(int i = 1; i < n; i++) {
		int u, v, w; scanf("%d%d%d", &u, &v, &w);
		edges[ecnt] = Edge(v, w, head[u]); head[u] = ecnt++;
		edges[ecnt] = Edge(u, w, head[v]); head[v] = ecnt++;
	}

	int white = n;
	ecnt = 0;
	memset(tmp, -1, sizeof(tmp));
	rebuild(1, 0);
	memcpy(head, tmp, sizeof(tmp));

	divide(1, n);

	m = ecnt >> 1;
	make_heap(heap, heap + m);
	for(int i = 0; i < m; i++) pos[heap[i].S] = i;

	int _; scanf("%d", &_);
	while(_--) {
		scanf("%s", op);
		if(op[0] == 'A') {
			if(!white) puts("They have disappeared.");
			else if(white == 1) puts("0");
			else printf("%d\n", max(heap[0].F, 0));
		} else {
			int u; scanf("%d", &u);
			color[u] ^= 1;
			if(color[u]) white--; else white++;
			for(PII t : b[u]) {
				int s = t.F, d = t.S;
				if(!color[u]) PQ[s].push(MP(d, u));
				while(~PQ[s].top().S && color[PQ[s].top().S]) PQ[s].pop();
				heap[pos[s >> 1]].F = PQ[s].top().F + edges[s].w + PQ[s^1].top().F;
				down(pos[s >> 1]); up(pos[s >> 1]);
			}
		}
	}

	return 0;
}