BZOJ_2813_奇妙的Fibonacci_线性筛

BZOJ_2813_奇妙的Fibonacci_线性筛

Description

Fibonacci数列是这样一个数列：

F1 = 1， F2 = 1， F3 = 2 . . .

Fi = Fi-1 + Fi-2 (当 i >= 3)

pty忽然对这个古老的数列产生了浓厚的兴趣，他想知道：对于某一个Fibonacci数Fi，

有多少个Fj能够整除Fi (i可以等于j)，他还想知道所有j的平方之和是多少。

Input

第一行一个整数Q,表示Q个询问。

第二行四个整数:Q₁, A, B, C

第i个询问Q_i = (Q_i-1 * A + B) mod C + 1(当i >= 2)

Output

Ai代表第i个询问有多少个F_j能够整除F_Qi。

Bi代表第i个询问所有j的平方之和。

输出包括两行：

第一行是所有的Ai之和。

第二行是所有的Bi之和。

由于答案过大，只需要输出除以1000000007得到的余数即可。

Sample Input

2
2 2 1 8

Sample Output

6
55

HINT

对于100%的数据保证：Q <= 3*10^6，C <= 10^7，A <= 10^7，B <= 10^7，1 <= Q1<= C

---

结论：(fn,fm)=f(n,m)

证明直接上图片：

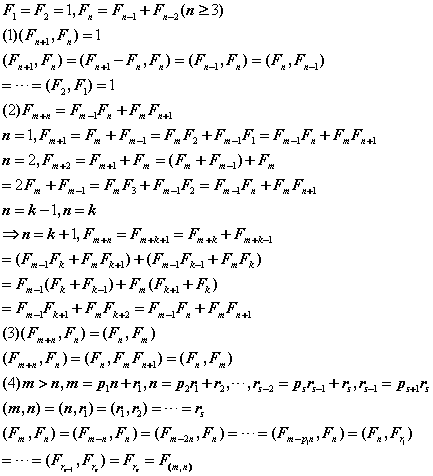
然后好办了。

fj|fi

(fi,fj)=fj

f(i,j)=fj

(i,j)=j 或  (i,j)=1且j=2。

线筛约数的平方之和，后面那个特判即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long long ll;
#define mod 1000000007
#define N 10000050
#define M 10000000
int prime[N],cnt,cs[N],ys[N];
ll pf[N];
bool vis[N];
void init() {
    ll i,j; ys[1]=pf[1]=1;
    for(i=2;i<=M;i++) {
        if(!vis[i]) {
            prime[++cnt]=i,cs[i]=i,ys[i]=2,pf[i]=(ll(i)*i+1)%mod;
            for(j=i*i;j<=M;j*=i) {
                ys[j]=ys[j/i]+1;
                pf[j]=(pf[j/i]+j*j)%mod;
            }
        }
        for(j=1;j<=cnt&&i*prime[j]<=M;j++) {
            int y=i*prime[j];
            vis[y]=1;
            if(i%prime[j]==0) {
                cs[y]=cs[i]*prime[j];
                if(i!=cs[i]) {
                    pf[y]=pf[i/cs[i]]*pf[prime[j]*cs[i]]%mod;
                    ys[y]=ys[i/cs[i]]*ys[prime[j]*cs[i]];
                }
                break;
            }
            cs[y]=prime[j];
            pf[y]=pf[i]*pf[prime[j]]%mod;
            ys[y]=ys[i]*ys[prime[j]];
        }
    }
}
int main() {
    init();
    ll Q,A,B,C;
    int n;
    ll ans1=0,ans2=0;
    scanf("%d%lld%lld%lld%lld",&n,&Q,&A,&B,&C);
    A%=C; B%=C;
    while(n--) {
        // printf("%d %lld\n",ys[Q],pf[Q]);
        ans1+=ys[Q]+(Q&1); if(ans1>=mod) ans1-=mod;
        ans2+=pf[Q]+(Q&1)*4; if(ans2>=mod) ans2-=mod;
        Q=(Q*A+B)%C+1;
    }
    printf("%lld\n%lld\n",ans1,ans2);
}