衡量线性回归法的指标MSE, RMSE,MAE和R Square
衡量线性回归法的指标:MSE, RMSE和MAE
举个栗子:
对于简单线性回归,目标是找到a,b 使得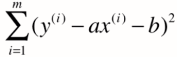 尽可能小
尽可能小
其实相当于是对训练数据集而言的,即
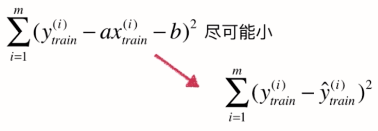
当我们找到a,b后,对于测试数据集而言
 ,理所当然,其衡量标准可以是
,理所当然,其衡量标准可以是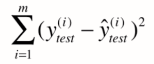
但问题是,这个衡量标准和m相关。
(当10000个样本误差累积是100,而1000个样本误差累积却达到了80,虽然80<100,但我们却不能说第二个模型优于第一个)
改进==> 对式子除以m,使得其与测试样本m无关
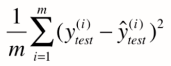 ->
-> 
但又有一个问题,之前算这个公式时为了保证其每项为正,且可导(所以没用绝对值的表示方法),我们对式子加了一个平方。但这可能会导致量纲的问题,如房子价格为万元,平方后就成了万元的平方。
又改进==> 对MSE开方,使量纲相同
 ->
->
MSE与RMSE的区别仅在于对量纲是否敏感
又一思路,通过加绝对值
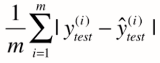 ->
-> 
在推导a,b的式子时(对train数据集),没用求绝对值的方法是因为其不是处处可导,不方便用来求极值。但评价模型时,对test数据集我们完全可以使用求绝对值的方式。
P.S. 评价模型的标准和训练模型时最优化的目标函数是可以完全不一样的。
RMSE vs MAE
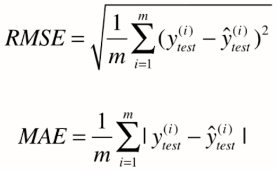
RMSE 与 MAE 的量纲相同,但求出结果后我们会发现RMSE比MAE的要大一些。
这是因为RMSE是先对误差进行平方的累加后再开方,它其实是放大了较大误差之间的差距。
而MAE反应的就是真实误差。因此在衡量中使RMSE的值越小其意义越大,因为它的值能反映其最大误差也是比较小的。
衡量线性回归法最好的指标 R Squared
对于上述的衡量方法,如RMSE和MAE还是有问题的,还是因为量纲不一样。比如我们预测考试分数误差是10,预测房价误差是1w。但我们却不能评价我们的模型是更适合预测分数还是预测房价。
解决方法==> 新的指标:R方
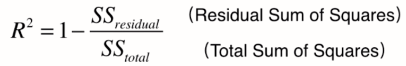
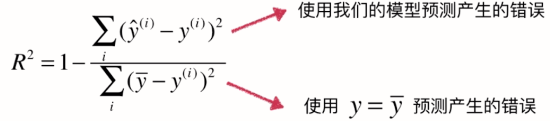
(上:y预测-y真,our model,下:y真平均-y真,baseline model)
使用baseline模型肯定会产生很多错误,我们自己的模型产生的错误会少一些。
1 - ourModelError / baselineModelError = 我们模型拟合住的部分

R方将回归结果归约到了0~1间,允许我们对不同问题的预测结果进行比对了。

我们可发现,上面其实就是MSE,下面就是方差
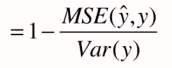
衡量线性回归法的指标MSE, RMSE,MAE和R Square的更多相关文章
- 【笔记】衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square
衡量线性回归法的指标 MSE,RMS,MAE以及评价回归算法 R Square 衡量线性回归法的指标 对于分类问题来说,我们将原始数据分成了训练数据集和测试数据集两部分,我们使用训练数据集得到模型以后 ...
- 机器学习:衡量线性回归法的指标(MSE、RMSE、MAE、R Squared)
一.MSE.RMSE.MAE 思路:测试数据集中的点,距离模型的平均距离越小,该模型越精确 # 注:使用平均距离,而不是所有测试样本的距离和,因为距离和受样本数量的影响 1)公式: MSE:均方误差 ...
- 可决系数R^2和MSE,MAE,SMSE
波士顿房价预测 首先这个问题非常好其实要完整的回答这个问题很有难度,我也没有找到一个完整叙述这个东西的资料,所以下面主要是结合我自己的理解和一些资料谈一下r^2,mean square error 和 ...
- 第3章 衡量线性回归的指标:MSE,RMSE,MAE
, , ,, , , ,
- 线性回归中常见的一些统计学术语(RSE RSS TSS ESS MSE RMSE R2 Pearson's r)
TSS: Total Sum of Squares(总离差平方和) --- 因变量的方差 RSS: Residual Sum of Squares (残差平方和) --- 由误差导致的真实值和估计值 ...
- SSE,MSE,RMSE,R-square指标讲解
SSE(和方差.误差平方和):The sum of squares due to errorMSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...
- SSE,MSE,RMSE,R-square 指标讲解
SSE(和方差.误差平方和):The sum of squares due to error MSE(均方差.方差):Mean squared errorRMSE(均方根.标准差):Root mean ...
- Data Mining: SSE,MSE,RMSE,R-square指标讲解
转载自:http://blog.csdn.net/l18930738887/article/details/50629409 SSE(和方差.误差平方和):The sum of squares due ...
- C / C ++ 基于梯度下降法的线性回归法(适用于机器学习)
写在前面的话: 在第一学期做项目的时候用到过相应的知识,觉得挺有趣的,就记录整理了下来,基于C/C++语言 原贴地址:https://helloacm.com/cc-linear-regression ...
随机推荐
- 常用css和js组件
1 . input框中插入图标 <div class="col-sm-12 col-xs-12 setLineHeight"> <div class=" ...
- Docker搭建
环境基于CentOS64位,内核最好3.10. 1.下载安装 docker dockersudo yum install docker-io (假如内核版本太低的话,会在下载安装Docker ...
- LoadRunner使用(1)
一.LoadRunner脚本录制 LoadRunner测试分为两个步骤: 第一步:录制脚本,其实就是监控并记录这段时间发送的HTTP请求 第二步:启动多个线程,用录制的脚本,模拟多线程发送请求. (1 ...
- HDU 5451 Best Solver(fibonacci)
感谢这道题让我复习了一遍线代,还学习了一些奇奇怪怪的数论. 令 二项展开以后根号部分抵消了 显然有 所以要求的答案是 如果n比较小的话,可以直接对二项式快速幂,但是这题n很大 这个问题和矩阵的特征值以 ...
- Centos7.3 安装devstack stein版本
1. 系统准备 # 关闭防火墙 systemctl stop firewalld systemctl disable firewalld # 关闭selinux setenforce 0 sed -i ...
- Js笔记-第11课
// 第11课 作用域精解 运行期上下文,当函数执行时,会创建一个成为执行期上下文的内部对象.一个执行期上下文定义了一个函数执行时的环境,函数每次执行时对应的执行期上下文都是独 ...
- (73)zabbix用户认证方式 内建、HTTP Basic、LDAP
公司大大小小众多系统,不同系统不同的账号密码,管理上相当复杂,后来慢慢出现了SSO等账号统一验证,其他zabbix也提供了类似的方法,或许有些公司便可以使用公司提供的账号来登录zabbix了. zab ...
- paper:synthesizable finite state machine design techniques using the new systemverilog 3.0 enhancements 之 standard verilog FSM conding styles(三段式)
Three always block style with registered outputs(Good style)
- 03 Django视图
功能 接受Web请求HttpRequest,进行逻辑处理,与 M 和 T 进行交互,返回 Web 响应 HttpResponse 给请求者 示例项目的创建 创建项目 test3 django-admi ...
- LeetCode(226)Invert Binary Tree
题目 分析 交换二叉树的左右子树. 递归非递归两种方法实现. AC代码 class Solution { public: //递归实现 TreeNode* invertTree(TreeNode* r ...
