BZOJ 2959: 长跑 LCT_并查集_点双

Description

　　某校开展了同学们喜闻乐见的阳光长跑活动。为了能“为祖国健康工作五十年”，同学们纷纷离开寝室，离开教室，离开实验室，到操场参加3000米长跑运动。一时间操场上熙熙攘攘，摩肩接踵，盛况空前。
　　为了让同学们更好地监督自己，学校推行了刷卡机制。
　　学校中有n个地点，用1到n的整数表示，每个地点设有若干个刷卡机。
　　有以下三类事件：
　　1、修建了一条连接A地点和B地点的跑道。
　　2、A点的刷卡机台数变为了B。
　　3、进行了一次长跑。问一个同学从A出发，最后到达B最多可以刷卡多少次。具体的要求如下：
　　当同学到达一个地点时，他可以在这里的每一台刷卡机上都刷卡。但每台刷卡机只能刷卡一次，即使多次到达同一地点也不能多次刷卡。
　　为了安全起见，每条跑道都需要设定一个方向，这条跑道只能按照这个方向单向通行。最多的刷卡次数即为在任意设定跑道方向，按照任意路径从A地点到B地点能刷卡的最多次数。

Input

　　输入的第一行包含两个正整数n,m，表示地点的个数和操作的个数。
　　第二行包含n个非负整数，其中第i个数为第个地点最开始刷卡机的台数。
　　接下来有m行，每行包含三个非负整数P,A,B，P为事件类型，A,B为事件的两个参数。
　　最初所有地点之间都没有跑道。
　　每行相邻的两个数之间均用一个空格隔开。表示地点编号的数均在1到n之间，每个地点的刷卡机台数始终不超过10000，P=1,2,3。

Output

　　输出的行数等于第3类事件的个数，每行表示一个第3类事件。如果该情况下存在一种设定跑道方向的方案和路径的方案，可以到达，则输出最多可以刷卡的次数。如果A不能到达B，则输出-1。

题解:

考虑什么时候会产生点双：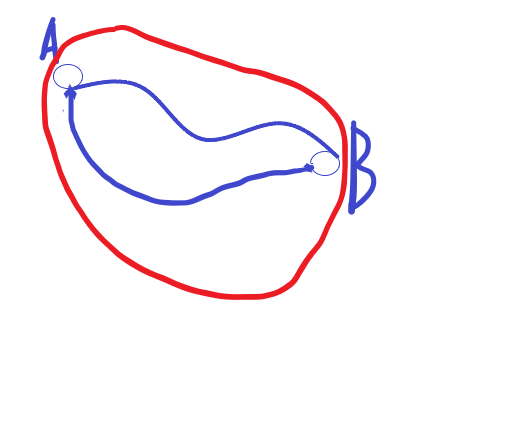

即 A,B 已联通，在 A,B 之间连一条边，则 A,B 与新边构成的环就是一个双联通分量（即一次可以全部到达的).

那么，我们就将这个环缩成一个点，把环中权值和赋值给环中一点.

由于只有加边操作，这种做法是没有什么问题的.
当我们每次在进行各种操作时，要先在并查集中 find 一下祖先（一个点可能事先被缩进一个点双集合里了）. 

#include<bits/stdc++.h>
#define maxn 1000000
using namespace std;
void setIO(string a)
{
    string in=a+".in",out=a+".out";
    freopen(in.c_str(),"r",stdin);
}
struct Union
{
    int p[maxn];
    void init() { for(int i=0;i<maxn;++i) p[i]=i;  }
    int find(int x) { return p[x]==x?x:p[x]=find(p[x]); }
    // 1 : disconnect
    // 0 : connect
    int merge(int x,int y)
    {
        int a=find(x),b=find(y);
        if(a!=b) { p[a]=b;  return 1; }
        return 0;
    }
}tree,con;
int n,Q;
int val[maxn],sumv[maxn];
#define lson ch[x][0]
#define rson ch[x][1]
#define get(x) (ch[f[x]][1]==x)
#define isRoot(x) (1^(ch[f[x]=tree.find(f[x])][1]==x||ch[f[x]=tree.find(f[x])][0]==x))
int ch[maxn][2],f[maxn],rev[maxn],sta[maxn],value[maxn];
void pushup(int x){ sumv[x]=sumv[lson]+sumv[rson]+val[x];  }
void mark(int x)
{
    if(!x) return;
    swap(lson,rson),rev[x]^=1;
}
void push(int x)
{
    if(!x||!rev[x]) return;
    mark(lson),mark(rson),rev[x]^=1;
}
void rotate(int x)
{
    int old=f[x],fold=f[old],which=get(x);
    if(!isRoot(old)) ch[fold][ch[fold][1]==old]=x;
    ch[old][which]=ch[x][which^1],f[ch[old][which]]=old;
    ch[x][which^1]=old,f[old]=x,f[x]=fold;
    pushup(old),pushup(x);
}
void splay(int x)
{
    x=tree.find(x);
    int v=0,u=x,fa;
    sta[++v]=u;
    while(!isRoot(u)) sta[++v]=(f[u]=tree.find(f[u])), u=f[u];
    while(v) push(sta[v--]);
    for(u=tree.find(f[u]); (fa=f[x])!=u; rotate(x))
        if(f[fa]!=u)
            rotate(get(fa)==get(x)?fa:x);
}
void Access(int x)
{
    int t=0;
    x=tree.find(x);
    while(x) splay(x),rson=t,pushup(x), t=x,x=(f[x]=tree.find(f[x]));
}
void MakeRoot(int x)
{
    x=tree.find(x), Access(x), splay(x), mark(x);
}
void split(int x,int y)
{
    x=tree.find(x),y=tree.find(y), MakeRoot(x), Access(y), splay(y);
}
void DFS(int x,int tp)
{
    if(!x) return;
    tree.p[x]=tp,DFS(lson,tp), DFS(rson,tp);
    ch[tp][0]=ch[tp][1]=rev[tp]=0;
}
void link(int x,int y)
{
    x=tree.find(x),y=tree.find(y), MakeRoot(x), f[x]=y;
}
int main()
{
    // setIO("input");
    tree.init(), con.init();
    scanf("%d%d",&n,&Q);
    for(int i=1;i<=n;++i) scanf("%d",&val[i]),value[i]=sumv[i]=val[i];
    while(Q--)
    {
        int p,a,b,x,y;
        scanf("%d%d%d",&p,&a,&b);       // point a -> point b
        switch(p)
        {
            case 1 :
            {
                a=tree.find(a), b=tree.find(b);
                if(con.merge(a,b)) link(a,b);
                else
                {
                    // 不属于同一点双
                    if(a!=b)
                    {
                        split(a,b), val[b]=sumv[b], DFS(b,b);
                    }
                }
                break;
            }
            case 2 :
            {
                x=a, a=tree.find(a);
                Access(a), splay(a), val[a]+=b-value[x],pushup(a),value[x]=b;
                break;
            }
            case 3 :
            {
                a=tree.find(a),b=tree.find(b);
                if(con.find(a)!=con.find(b)) printf("-1\n");
                else
                {
                    split(a,b), printf("%d\n",sumv[b]);
                }
                break;
            }
        }
    }
    return 0;
}