Binary Indexed Tree 总结

特点

1. 针对 数组连续子序列累加和 问题（需要进行频繁的 update、sum 操作）；

2. 并非是树型结构，只是逻辑上层次分明；

3. 可以通过 填坑法 来理解；

4. 中心思想：每一个整数都可以由几个 二进制指数的相加和 来进行唯一表示。

中心思想

每一个整数都可以由几个二进制指数的相加和唯一表示：

11    =  2^3  +  2^1  +  2^0
01011 = 01000 + 00010 + 00001 //二进制表示

在Binary Indexed Tree 中，上述的思想应用体现在：

我们需要下标为 1~11 的元素的累加和， 要 1~8 的累加和，加上 9~10 的累加和， 最后加上 11 的累加和。

填坑法图解 Binary Indexed Tree

数组例子：

数组:[ 0, 2, 0, 1, 1, 1, 0, 4, 4, 0, 1, 0, 1, 2, 3, 0 ]
下标:    2  3  4  5  6  7  8  9  10 11 12 13 14 15 16

为了简化后续操作，我们将上例中数组下标改为从 1 开始。

第一层：在1~16区间内，在下标为 2的指数 的BIT数组元素位置中，填充  从1开始 到 所有下标为  2的指数（1, 2，4,，8，16） 的区间和。

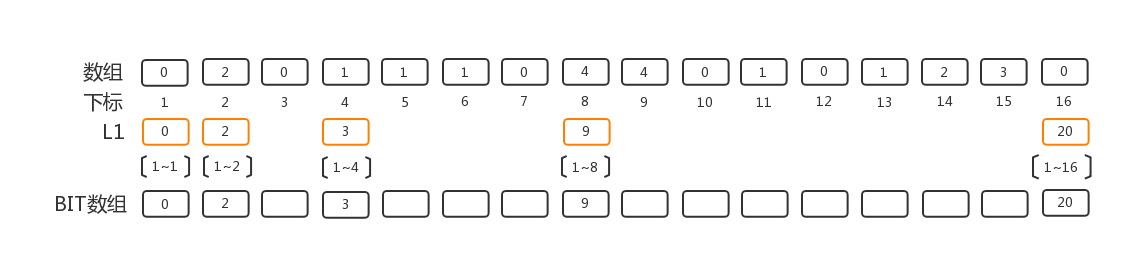
第二层：在所有未填充区间中，设每个区间开头下标为 start，在下标为 start+2的指数 的BIT数组元素位置中，填充 从start开始 到 下标为 start+2的指数 的区间和。

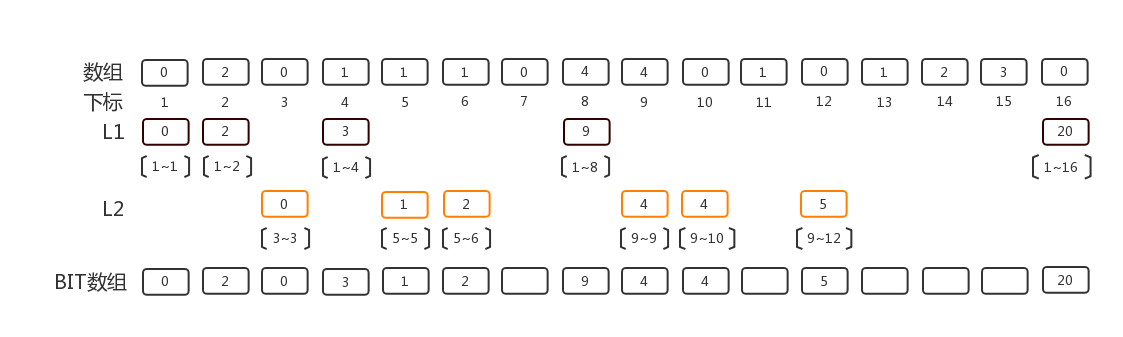
第三层，依照第二层的填坑方法类推，填充 7~7， 11~11， 13~15 区间。

第四层，以此类推，填充最后一个 坑 15~15。

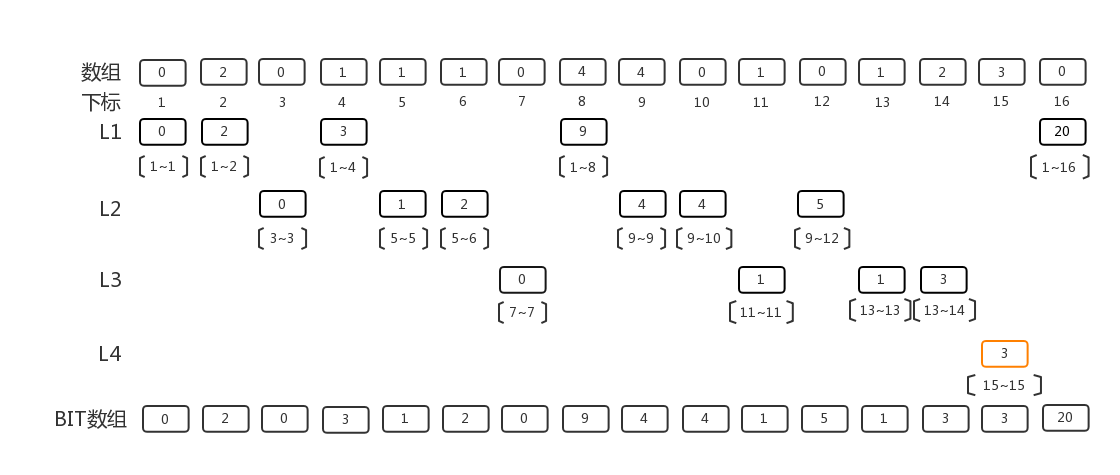
从上述过程可以看出，Binary Indexed Tree 实际上是个层次分明的结构。

从填坑法的角度来看，就是在每个坑中的第1、2、4、8、16……个位置上，填入从 坑的 start 位置 到 该位置 上所有元素的 sum 值；

第一层只有一个大坑，而第二层的坑 则是第一层填坑后留下的所有空洞位置；第三层的坑则是第一层和第二层填补后留下的所有空洞位置……

从下标的二进制表示来看，坑就是 0 的位置（多个 0 聚一起形成一个大坑）：

第一层      00000 （这里假设第一层是一个大坑）
填坑　　    0000 （1）
　　　　　　 0000 （2）
　　　　　　 0000 （4）
　　　　　　 0000 （8）
　　　　　　 0000 （16）

第二层   00001          00010           00100            01000            10000 （第二层有3个坑）
---------------------------------------------------------------------------------------------

填坑 　 　无            0001（3）       0010 （5）       0100 （9）         无
                                       0010 （6）      0100 （10）
                                                       0100 （12）   

……

注意区分几个概念：

1. 坑是指什么？从什么位置开始，到什么位置结束？-->下标二进制表示中 0 的聚合形成坑

2. 在BIT数组中填充的究竟是什么？ --> 某个坑中从 坑的开始位置 到 该BIT数组下标位置 的区间和

3. 如果确定每一层要操作的BIT数组下标？
   --> 可以根据下标的二进制表示，先确定坑有多大，再把坑中最后一个0变为1，然后把这个1依次左移，直到到达坑的开始位置；
       就可以得到一系列需要填充的区间结束位置，结合坑的开始位置，计算出该区间的和，填入 BIT[区间结束位置] 中。

Sum 操作

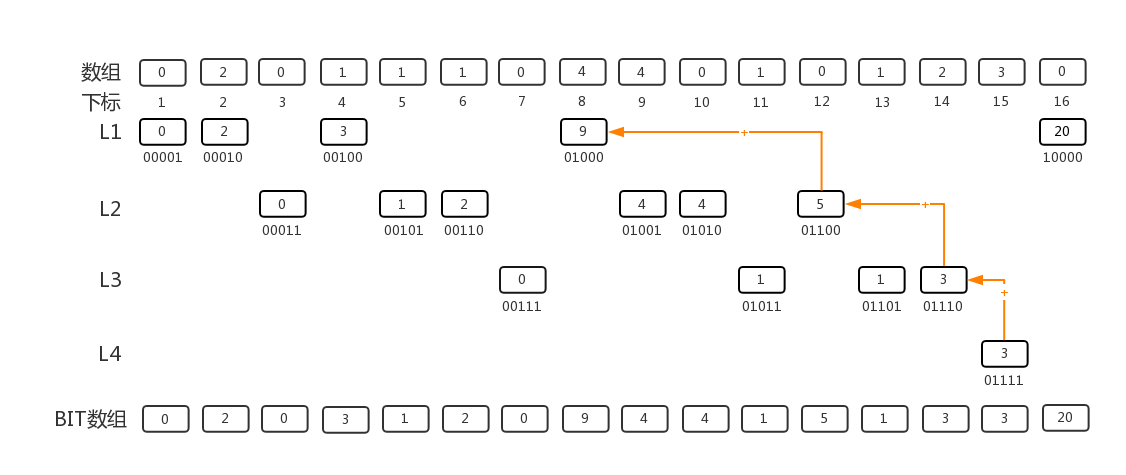
数字操作原理：

15 -> 14 -> 12 ->8
01111 -> 0111 -> 0110 -> 0100  //从右往左，依次把 1 反转为 0
15 = 01000 （1-8） + 00100 （9-12） + 00010 （13-14） + 00001 （15）

代码实现：

求 1~K 区间和
从 K 开始，依次翻转 K 的二进制表示 的最后一个 1 来获取 K1， K2， ……直至归零，然后：
Sum(1~K) = BIT[K] + BIT[K1] + BIT[K2] + ......

翻转最后一个 1 的小技巧：

利用补码
15的补码：       00001111
-15的补码：      11110001
两者按位相与，得到 00000001，即15二进制表示的最后一位1
所以直接让 15 减去 得到的这最后一位1就好。

所以推导下一位的代码是：

BIT[K] = BIT[K - (K & -K)]

时间复杂度

O(logn)

 Update 操作

对数组下标6的元素 +2示例：

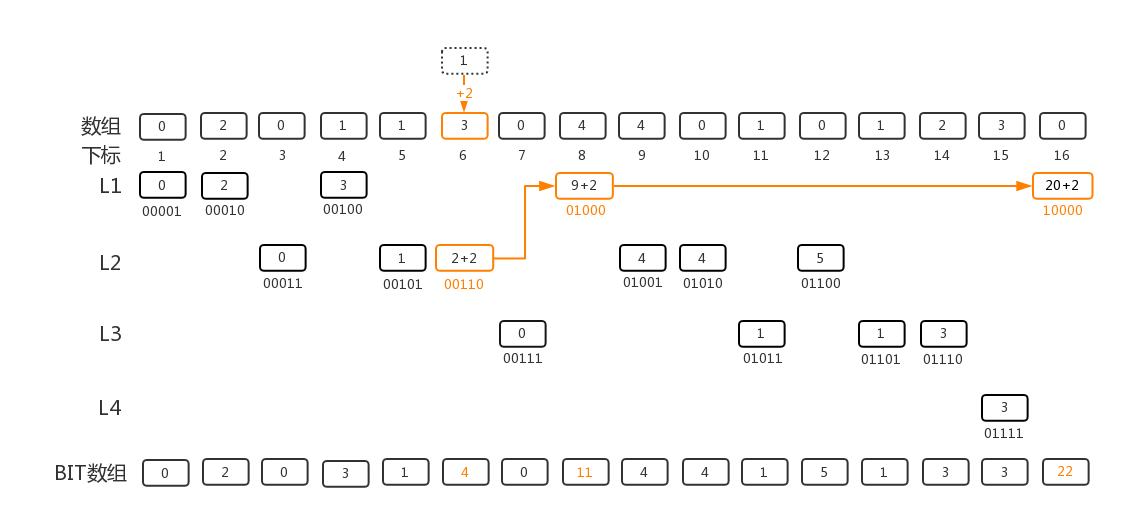
数字操作原理：

6 -> 8 ->16
00110 -> 01000 -> 10000
00110 + 00010 = 01000
01000 + 01000 = 10000
//让 K 加上其二进制表示的最后一位 1 形成的数字，即可推导出下一项的下标

推导下一项代码实现：

BIT[K] = BIT[K + (K & -K)]

时间复杂度：

O(logn)

Binary Indexed Tree的建立

把初始数组设为全为 0 的数组，然后依次把数组中的元素进行一次 update操作，就完成了 BIT 数组的构建。

时间复杂度：

O(nlogn)

其他观察

以 1 为初始下标，BIT数组中的奇数下标的元素都是直接存了原数组元素的值，而偶数下标的原数组的值也可以通过BIT数组在比较小的消耗情况下得到。

所以，Binary Indexed Tree在一定效率容忍情境下，可以用BIT数组取代原数组，不必保留原数组（省去空间）

BIT数组还可以被拓展到多维的应用？？？？（后续看到相关资料将补充）

参考链接：https://www.cnblogs.com/whensean/p/6851018.html