8、Situation-Dependent Combination of Long-Term and Session-Based Preferences in Group Recommendations: An Experimental Analysis ----组推荐中基于长期和会话偏好的情景依赖组合

一、摘要：

背景：会话组推荐系统的一个主要挑战是如何适当地利用群组成员之间的交互引起用户偏好，这可能会偏离用户的长期偏好。长期偏好和群组诱导的偏好之间的相对重要性应该根据具体的群组设置而变化。

本文：通过实验，结论：当群组讨论对群组成员的喜好没有影响时，长期偏好占有更大权重。而当群组上下文促使成员有更多或更少的相似喜好时，群组诱导偏好占有更大权重。

二、引言：

背景：传统的推荐系统注重于个性化推荐，但是现在存在许多需要满足一组用户需求的场景。例如，一群朋友或者一个家庭需寻找一个餐厅，这导致了群组推荐系统的发展。

问题：群组推荐系统在提高推荐质量的研究已经有了一定的进展，但是群组决策过程的动态性还没有得到充分的探索。事实上，大多数研究都注重融合群组成员静态偏好的方法，这些方法忽略了在特定组上下文中用户的行为，并且忽略了用户偏好的变化，【这些变化经常发生在群组决策过程中】

本文：提出一个会话群组重修正模型，该模型既考虑了个体的长期偏好【由项目评分获得】，还考虑了用户在群组讨论期间对项目的直接反馈【其反应了用户当前的需求】。该模型是在一个提供聊天环境的群组推荐系统中实现的，该推荐系统集成了各种决策支持和重新通知的功能。

在该系统可能存在群组成员面对群组情景有不同的社会表现。例如：群组成员可以根据个人想法表达自己观点，也可以改变自己的观点以接受他人的影响，或者他们采取与团队建议相反的行动。

本文的目的：研究如何在上述场景中适当地结合长期偏好和会话特定的偏好。

三种社会影响：（a）独立性——群组对用户偏好没有影响。（b）转换——群组推动成员之间有更多相似的偏好。（c）反一致性——群组使成员有更多的不同偏好。

偏好组合战略的三个变体：（一）长期和基于会话偏好的重要性相等（二）长期偏好更重要（三）会话偏好更重要。

三、群组推荐

在以往的模型中，组推荐系统通过项目评分来获得长期偏好，但是，在群组讨论中，群组成员可能偏离他们之前所观察到的偏好。这可能是由于其他群组成员和群组决策动态的影响。

因此，需利用两个偏好来生成且持续更新用户的偏好模型。

• 成员偏好模型由函数来表示，
• 对群组成员的效用函数进行聚合，建立群组偏好模型。
• 根据该组偏好来对群组推荐项目进行排序。

每个用户的偏好模型由效用函数表示：

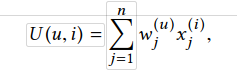
这里 x(i) = (x1(i), . . . , xn(i))是一个n维bool特征向量，其表示项目i。 xj(i) = 1 (xj(i) = 0) 表示项目有（无）第j个特征。例如：

x(5) = （1，0，1，0）意味着项目5包含第1和第3个特征，没有第2和第4个特征。

w表示用户偏好，权重。w_j^（u）表示用户u对第j个项目特征的重要程度。所有权重相加等于1，且大于0，越大越重视。

1、基于内容的方法生成表示用户的长期偏好的效用向量：

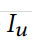是由用户u打分的项目集合，K是归一化因子。例如：

2、会话偏好

当群组决策过程中，假设用户为群组讨论提出项目并评估其他群组成员提出的项目。

在小组讨论中，所有项目被分为四组：BS（u）（最佳项目）、LS（u）（喜欢项目）、NS（u）（中性项目）、DS（u）（不喜欢项目）。

假设用户偏好具有较大效用的项，故以下满足约束：

：群组g中用户u的项目效用集合。

比如：

3、用户和群组的效用函数：

用户u的群组会话偏好：

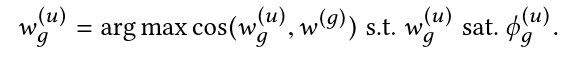
w (g)表示群组所有成员的平均会话偏好。wg(u)需要满足约束，同时与w(g)的余弦相似度最大。

原始用户长期偏好和会话偏好的线性组合：

以下表示用户长期偏好受群组诱导偏好的影响，产生的真实效用向量。其中，γ就是控制偏好组合三个变体的参数。

整体算法：