matlab 求解线性规划问题

线性规划 LP（Linear programming，线性规划）是一种优化方法，在优化问题中目标函数和约束函数均为向量变量的线性函数，LP问题可描述为：

• minf(x)：待最小化的目标函数（如果问题本身不是最小化问题，则应做适当转换，使其变为最小化问题，比如如果原始问题是最大化的话，目标函数 f = -f）
• A⋅x≤b：不等式约束
• Aeq⋅x=beq：等式约束
• lb≤x≤ub：取值范围约束（lb：lower bound，ub：upper bound）

[x, fval] = linprog(f,A,b,Aeq,beq,lb,ub)

2. 线性规划模型的三要素

• 1）决策变量：需决策的量，即待求的未知数（x），
• 2）目标函数：需优化的量，即欲达的目标，用决策变量的表达式表示（即目标函数是关于决策变量的函数 f(x)）
• 3）约束条件：为实现优化目标需受到的限制，用决策变量的等式（Aeq⋅x=beq）或者不等式表示（Ax≤b）

3. 使用 matlab 求解实际问题

一定要明确其中 A, b; Aeq, beq; lb, ub

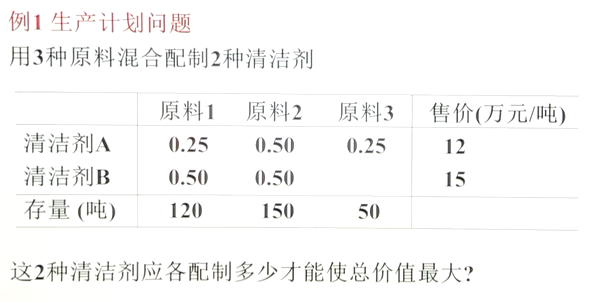
也即求解如下问题：

max12x+15y,s.t.0.25x+0.5y≤1200.5x+0.5y≤1500.25x≤50x≥0,y≥0

f = [-12, -15];
A = [.25, .5; .5, .5; .25, 0]; b = [120; 150; 50];
lb = [0; 0];
[x, fval] = linprog(f, A, b, [], [], lb, []);