SLAM概念学习之随机SLAM算法
这一节,在熟悉了Featue maps相关概念之后,我们将开始学习基于EKF的特征图SLAM算法。
1. 机器人,图和增强的状态向量
随机SLAM算法一般存储机器人位姿和图中的地标在单个状态向量中,然后通过一个递归预测和量测过程来估计状态参数。其中,预测阶段通过增量航迹估计来处理机器人的运动,并增加了机器人位姿不确定性的估计。当再次观测到Map中存储的特征后,量测阶段,或者叫更新阶段开始执行,这个过程可以改善整个的状态估计。当机器人在运动过程中观测到新特征时,便通过一个状态增强的过程将新观测的特征添加到状态向量中。
机器人的状态,即一个相对于参考笛卡尔坐标系的自身位姿参数通过均值和协方差来定义:
 (1)
(1)
 (2)
(2)
图的协方差矩阵Pm 包含特征之间的互相关信息(即非对角项),这些交叉关联信息表征了每个特征对Map中其他特征相关信息的依赖。由于特征的位置是静态的,当周围的环境也即Map是刚性的话,特征之间的交叉关联将会随着的特征的二次观测增强。图中的特征可以表示如下
 (3)
(3)
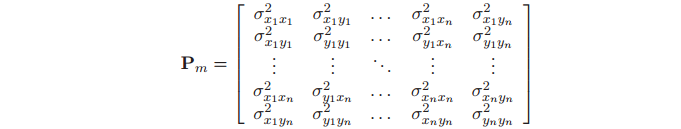 (4)
(4)
SLAM中的图通过一个串联了机器人位姿和特征图状态的增强状态向量定义,如图1所示。这是很有必要的,因为一致的SLAM依赖于机器人位姿和图之间相关性Pvm
 (5)
(5)
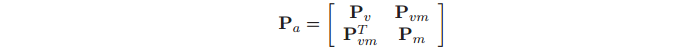 (6)
(6)

Fig. 1 增强的状态向量.
需要注意的是,状态的初始化时通常为 和
和 .也就是说,还没有特征被机器人观测到,并且初始时刻机器人位于参考坐标系的原点。
.也就是说,还没有特征被机器人观测到,并且初始时刻机器人位于参考坐标系的原点。
2. 预测阶段
随机SLAM算法的过程模型根据航迹推算运动估计来确定机器人相对于先前时刻位姿的运动,图特征仍然保持静止。这个模型对状态估计的影响存在于状态向量 部分和状态协方差矩阵中的
部分和状态协方差矩阵中的 以及
以及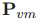 项。而
项。而 和
和 这些图特征相关项仍保持不变。
这些图特征相关项仍保持不变。
估计带来的机器人(这里以移动小车为例)位姿变化 和协方差
和协方差 通常用车轮的编码器测量和小车对应的运动学模型获取。本文里面的位姿改变通过基于激光测距的航迹推算获取,该算法可以通过批处理数据关联算法来找出序列激光扫描之间的相对位姿关系。
通常用车轮的编码器测量和小车对应的运动学模型获取。本文里面的位姿改变通过基于激光测距的航迹推算获取,该算法可以通过批处理数据关联算法来找出序列激光扫描之间的相对位姿关系。

Fig. 2 机器人位姿变化示意.
因此,预测的增强状态可以表示为
 (7)
(7)
 (8)
(8)
其中,雅各比矩阵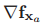 和
和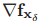 的定义为
的定义为
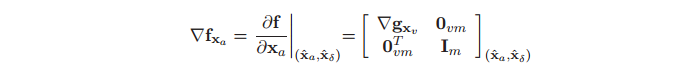 (9)
(9)
 (10)
(10)
雅各比矩阵 和
和 定义为
定义为
 (11)
(11)
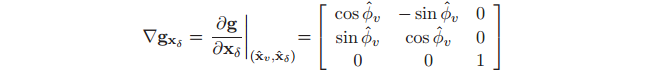 (12)
(12)
因为雅各比矩阵仅仅影响机器人的协方差矩阵 和对应的交叉相关性
和对应的交叉相关性 ,方程(8)用下式高效地实现
,方程(8)用下式高效地实现
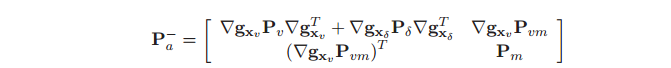 (13)
(13)
3. 更新阶段
如果已经存储在图中的估计特征 被距离方位传感器二次观测到,此时对应的量测量可以表示为
被距离方位传感器二次观测到,此时对应的量测量可以表示为
 (14)
(14)
 (15)
(15)
其中,量测量 分别表示对应的距离值和相对于观测机器人的偏转角度。
分别表示对应的距离值和相对于观测机器人的偏转角度。 为量测协方差。传感器获取的量测值和图之间的关联可以通过下面的方程表示
为量测协方差。传感器获取的量测值和图之间的关联可以通过下面的方程表示
 (16)
(16)
Kalman增益 可以得到
可以得到
 (17)
(17)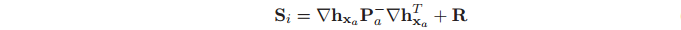 (18)
(18)
 (19)
(19)
其中,雅各比矩阵 为
为
 (20)
(20)
对于包含许多特征的SLAM图,雅各比矩阵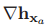 将会含有许多零项,这会使得方程(18)和(19)的计算非常高效。
将会含有许多零项,这会使得方程(18)和(19)的计算非常高效。
随后我们可以从更新过程得到一个后验SLAM估计
 (21/22)
(21/22)
实践表明,如果几个独立的量测同时可用,即知道 ,便有可能获取更加精确的更新。
,便有可能获取更加精确的更新。
4. 状态增强
当机器人在环境中漫游时,一旦新特征被观测到,就必须存储到图中。接下来将给出新观测到的特征初始化方法,首先,状态向量和对应的协方差矩阵通过新的量测的极值增强为
 (23)
(23)
 (24)
(24)
量测z 通过函数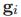 被转换位全局的笛卡尔坐标系特征位置,对应的变换表示如下
被转换位全局的笛卡尔坐标系特征位置,对应的变换表示如下
 (25)
(25)
可以通过线性化函数 将增强的状态初始化
将增强的状态初始化
 (26/27)
(26/27)
其中,雅克比矩阵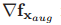 表示为
表示为
 (28)
(28)
与特征的储存相比,特征的删除非常简单,只需将特征对应的元素直接从状态向量删除,同时将相关的行和列中的项目从协方差矩阵中删除。
SLAM概念学习之随机SLAM算法的更多相关文章
- SLAM概念学习之特征图Feature Maps
特征图(或者叫地标图,landmark maps)利用参数化特征(如点和线)的全局位置来表示环境.如图1所示,机器人的外部环境被一些列参数化的特征,即二维坐标点表示.这些静态的地标点被观测器(装有传感 ...
- Bagging与随机森林算法原理小结
在集成学习原理小结中,我们讲到了集成学习有两个流派,一个是boosting派系,它的特点是各个弱学习器之间有依赖关系.另一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合. ...
- R语言︱决策树族——随机森林算法
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- 笔者寄语:有一篇<有监督学习选择深度学习 ...
- R语言︱机器学习模型评估方案(以随机森林算法为例)
笔者寄语:本文中大多内容来自<数据挖掘之道>,本文为读书笔记.在刚刚接触机器学习的时候,觉得在监督学习之后,做一个混淆矩阵就已经足够,但是完整的机器学习解决方案并不会如此草率.需要完整的评 ...
- Python机器学习笔记——随机森林算法
随机森林算法的理论知识 随机森林是一种有监督学习算法,是以决策树为基学习器的集成学习算法.随机森林非常简单,易于实现,计算开销也很小,但是它在分类和回归上表现出非常惊人的性能,因此,随机森林被誉为“代 ...
- 使用Numpy验证Google GRE的随机选择算法
最近在读<SRE Google运维解密>第20章提到数据中心内部服务器的负载均衡方法,文章对比了几种负载均衡的算法,其中随机选择算法,非常适合用 Numpy 模拟并且用 Matplotli ...
- H2O中的随机森林算法介绍及其项目实战(python实现)
H2O中的随机森林算法介绍及其项目实战(python实现) 包的引入:from h2o.estimators.random_forest import H2ORandomForestEstimator ...
- 用Python实现随机森林算法,深度学习
用Python实现随机森林算法,深度学习 拥有高方差使得决策树(secision tress)在处理特定训练数据集时其结果显得相对脆弱.bagging(bootstrap aggregating 的缩 ...
- 随机森林算法-Deep Dive
0-写在前面 随机森林,指的是利用多棵树对样本进行训练并预测的一种分类器.该分类器最早由Leo Breiman和Adele Cutler提出.简单来说,是一种bagging的思想,采用bootstra ...
随机推荐
- C# 特性(Attribute)
C# 特性(Attribute) 特性(Attribute)是用于在运行时传递程序中各种元素(比如类.方法.结构.枚举.组件等)的行为信息的声明性标签.您可以通过使用特性向程序添加声明性信息.一个声明 ...
- Android 多线程下载 显示进度 速度
功能要求:从网络下载一APK应用,显示下载速度.进度,并安装应用. 运行效果图: 工程结构图: 很简单,就一个activity,一个更新UI的线程,一个下载线程加个文件处理类 主要代码: /** *多 ...
- 五分钟DBA:浅谈伪分布式数据库架构
[IT168 技术]12月25日消息,2010互联网行业技术研讨峰会今日在上海华东理工大学召开.本次峰会以“互联网行业应用最佳实践”为主题,定位于互联网架构设计.应用开发.应用运维管理,同时,峰会邀请 ...
- 让html页面不缓存js的实现方法
很多朋友都会碰到这样的情况:如果我们页面加载了js的话下次打开时也会是调用这个js缓存文件,但对于我们调试时是非常的不方便了,本文就来谈论如何解决这一问题,下面一起来看看. 不缓存JS的方法其实挺简单 ...
- 自己写的PHP的mql类
用类封装的一个数据库的操作,不仅安全,而且会省去很多代码. header('Content-type:text/html;charset="utf-8"'); class mysq ...
- ZBrush通过显示与隐藏得到子物体
在ZBrush®中得到子物体的方法有很多,本文将为大家介绍一种新的创建子物体的方法,通过显示和隐藏得到子物. ZBrush 4R8中文版下载:http://wm.makeding.com/iclk/? ...
- 三、frpc 完整配置文件
# [common] is integral section [common] # A literal address or host name for IPv6 must be enclosed # ...
- 好文应该收藏-----redis 配置自启动
话不多说,请看原作者笔记,亲测,可用 https://blog.csdn.net/qq_42810276/article/details/81296012
- Redis windows版本的启停bat脚本命令
Reids windows版本安装 redis windows官网推荐:https://github.com/MicrosoftArchive/redis/releases 下载解压即可. 启停bat ...
- Hbase读取数据
get命令和HTable类的get()方法用于从HBase表中读取数据.使用 get 命令,可以同时获取一行数据.它的语法如下: get ’<table name>’,’row1’ 下面的 ...
