n阶方阵，数字从1~n^2，顺时针增大

运行结果如下图：

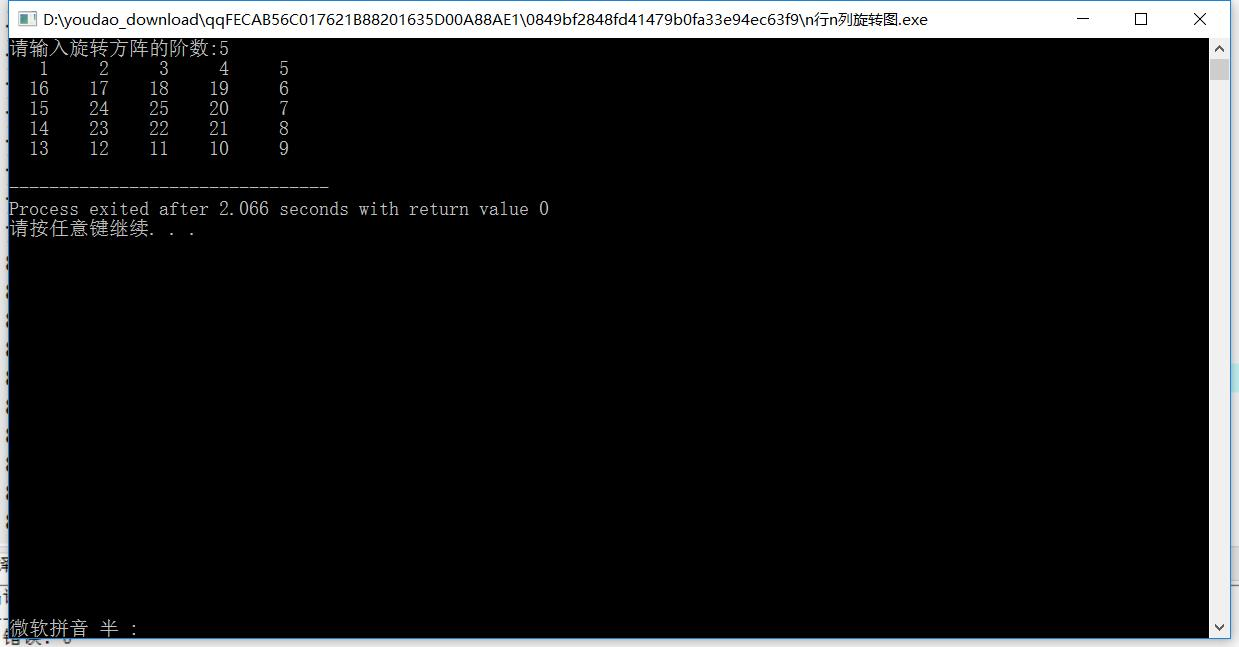
解题思路：可以将这个问题分解成x个外围正方形所围成的图形，外围的正方形又可以分为4个步骤，向右依次增大、向下依次增大、向左依次增大、向上依次增大。基本思路就是如此，最关键的就是什么时候是转折的时候，比如向右增大到接下来的向下增大转折条件是什么，我没细究所以给外围加了围墙（数组初始化为0，在输入n后在外围全赋值为1）作为判定条件，详细看代码

以下给出代码示例：

#include <stdio.h>//自己写的code 

#define N 20

//解决的问题：数字从1开始顺时针填入n行n列数组

int arrary[N][N]={0};

 

void assist(int);

void deal(int &,int,int);

 

int main()

{

    int row=1,column=1,i=row,j=column,n;

    int count=0,num=1;

    printf("请输入旋转方阵的阶数:"); 

    scanf("%d",&n);

    assist(n);

    while(count!=(n%2==0? n/2:n/2+1))

    {

    deal(num,row,column);

    count++; row++; column++;

    }

 

    for(i=1;i<=n;i++){

        for(j=1;j<=n;j++)

            printf("%4d  ",arrary[i][j]);        

        printf("\n");

    }

 

}

 

void assist(int n)//外加围墙

{

 

   for(int j=0;j<=n+1;j++)

   arrary[0][j]=1;

   for(int i=0;i<=n+1;i++)

   arrary[i][n+1]=1;

   for(int j=n+1;j>=0;j--)

    arrary[n+1][j]=1;

   for(int i=n+1;i>=0;i--)

    arrary[i][0]=1;

 }

 

 

void deal(int &num,int column,int row)

{

    int i,j;

    i=row;j=column;

    for(j=column;;j++)//右横

    {

    if(arrary[row][j])break;

    arrary[row][j]=num++;

    }column=j-1;

 //printf("column:%d\n",column);测试数据时候检测

    for(i=row+1;;i++)//下

    {

    if(arrary[i][column])break;

    arrary[i][column]=num++;

    }row=i-1;

//printf("row:%d\n",row);

    for(j=column-1;;j--)//左横

    {

    if(arrary[row][j])break;

    arrary[row][j]=num++;

    }column=j+1;

// printf("column:%d\n",column);

    for(i=row-1;;i--)//上

    {

    if(arrary[i][column])break;

    arrary[i][column]=num++;

    }row=i-1;

//printf("row:%d\n",row);

 }