P3398 仓鼠找sugar[LCA]

题目描述

小仓鼠的和他的基（mei）友（zi）sugar住在地下洞穴中，每个节点的编号为1~n。地下洞穴是一个树形结构。这一天小仓鼠打算从从他的卧室（a）到餐厅（b），而他的基友同时要从他的卧室（c）到图书馆（d）。他们都会走最短路径。现在小仓鼠希望知道，有没有可能在某个地方，可以碰到他的基友？

小仓鼠那么弱，还要天天被zzq大爷虐，请你快来救救他吧！

解析

当然可以树剖。

一开始想用路径长作为判断依据，但总是WA，下数据发现就错那么一个两个小问，也是很玄学。。。

于是转而研究点如何作为判断依据。

对于一个这样的树链，它的两端点为\(a,b\)，如下图。

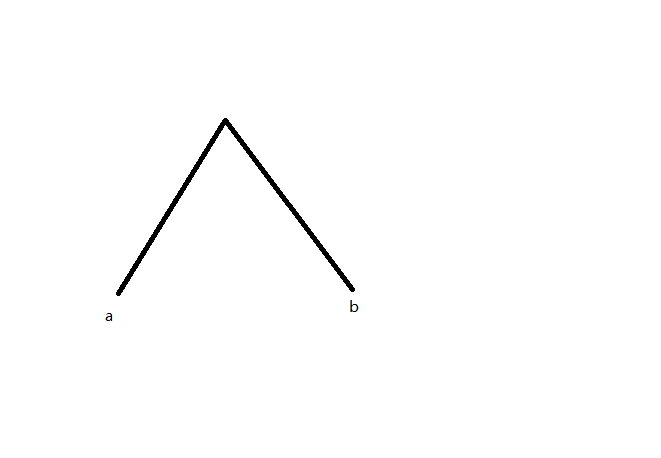
反过来想，如果我们要构造一条路径，使得树上某一个点到另一点的路径与现有路径相交，该如何做呢？

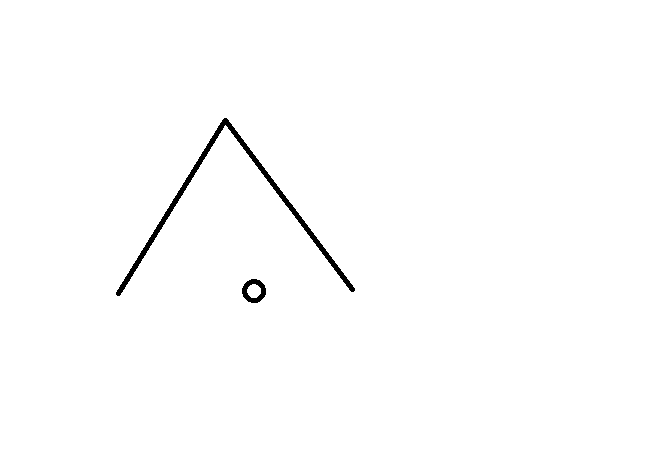
首先，这个点肯定要先有一部分路径连到原先的树链上吧，否则不可能相交。

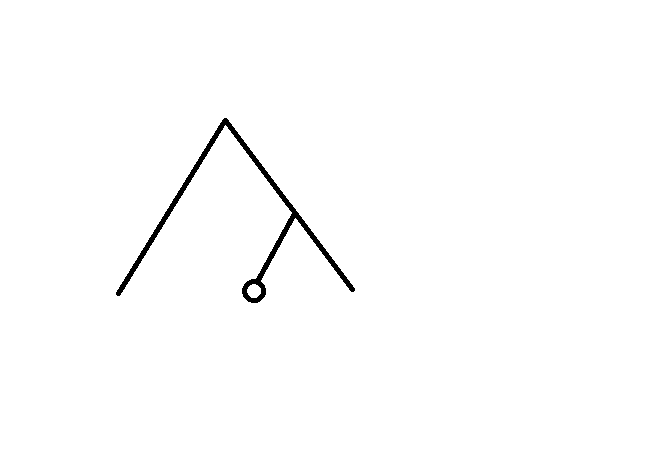
构造出的路径剩下的部分只可能是这三种情况。

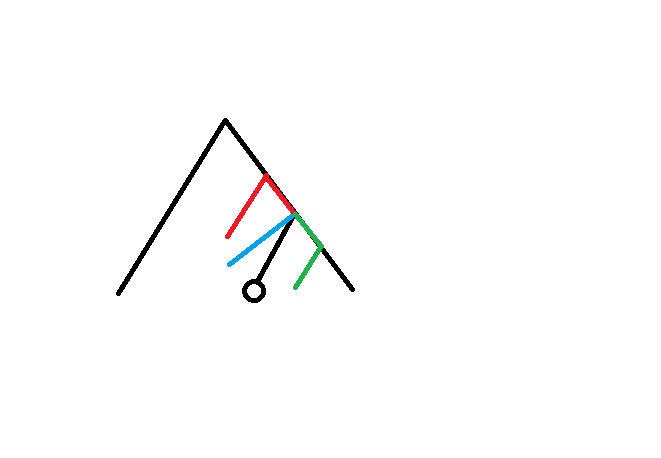
而如果这样构造路径就违反了树的定义。

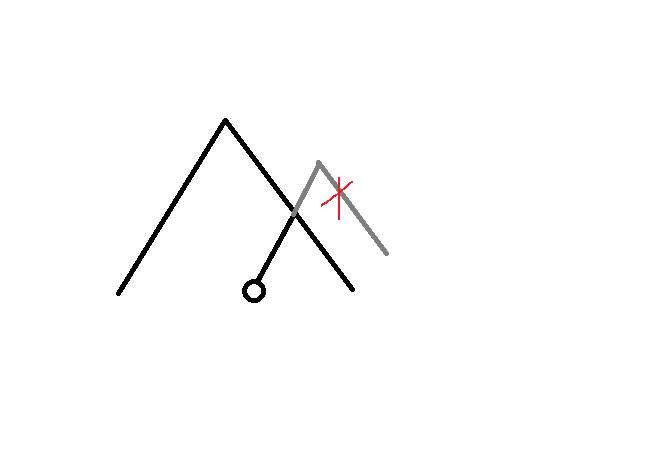
我们发现，构造出的路径一定有一个点在原树链上。但是这样还是不好下手，我们并不知道如何寻找这个点。

再进一步观察，发现新路径两端点的lca一定在原树链上。而lca很容易求，爱怎么求怎么求。

因此对于原问题，我们只需要判断某一对点的lca是否在另一对点表示的树链上即可。

判断一个点是否在一条树链上很容易，如果有一个点\(x\)，我们要判断它是否在\(a,b\)构成的树链

\((a,b)\)上，显然若

\[deep[x]>=deep[lca(a,b)]\&\&(lca(a,x)==x\| lca(b,x)==x)
\]

成立，那么\(x\)在\((a,b)\)上。

参考代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 100010
#define MOD 2520
#define E 1e-12
using namespace std;
inline int read()
{
	int f=1,x=0;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;
}
struct rec{
	int next,ver;
}g[N<<1];
int head[N],tot;
inline void add(int x,int y)
{
	g[++tot].ver=y;
	g[tot].next=head[x],head[x]=tot;
}
int f[21][N],dep[N],n,t;
inline void init()
{
	queue<int> q;
	q.push(1);dep[1]=1;
	while(q.size()){
		int x=q.front();q.pop();
		for(int i=head[x];i;i=g[i].next){
			int y=g[i].ver;
			if(dep[y]) continue;
			f[0][y]=x;dep[y]=dep[x]+1;
			for(int j=1;j<=t;++j)
				f[j][y]=f[j-1][f[j-1][y]];
			q.push(y);
		}
	}
}
inline int lca(int x,int y)
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int j=t;j>=0;--j)
		if(dep[f[j][x]]>=dep[y]) x=f[j][x];
	if(x==y) return x;
	for(int j=t;j>=0;--j)
		if(f[j][x]!=f[j][y]) x=f[j][x],y=f[j][y];
	return f[0][x];
}
int main()
{
	int q;
	n=read(),q=read();t=log2(n)+1;
	for(int i=1;i<n;++i){
		int u=read(),v=read();
		add(u,v),add(v,u);
	}
	init();
	while(q--){
		int a=read(),b=read(),c=read(),d=read();
		int k1=lca(a,b),k2=lca(c,d);
		if(dep[k1]>=dep[k2]&&(lca(c,k1)==k1||lca(d,k1)==k1)) puts("Y");
		else if(dep[k2]>=dep[k1]&&(lca(a,k2)==k2||lca(b,k2)==k2)) puts("Y");
		else puts("N");
	}
	return 0;
}