初探Android逆向：通过游戏APP破解引发的安全思考

如今移动互联网已经完全融入到我们的生活中，各类APP也是层出不穷，因此对于安卓APP安全的研究也尤为重要。本文通过对一款安卓APP的破解实例，来引出对于APP安全的探讨。（本人纯小白，初次接触安卓逆向一星期，略有体验，在这里分享一下）

本次破解的安卓APP是某款射击类游戏，我们发现在游戏里面有购买补给的功能，那么我们就针对这个功能进行破解，旨在达到免费购买。

首先，对该游戏进行还原，即反编译。反编译后可以查看该APP的配置文档、算法逻辑等，方便我们对其进行分析。在这里，我们使用工具AndroidKiller来对其进行反编译。

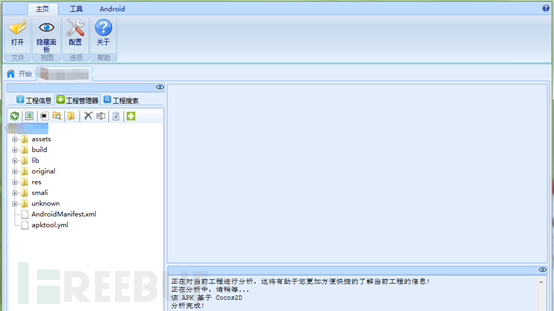
通过上图，可以看到APP的组成部分。我们只需要关注smali文件，因为Smali是安卓系统里的 Java 虚拟机（Dalvik）所使用的一种 dex 格式文件的汇编器。我们可以通过smali文件来查看APP的伪代码，从而了解其算法逻辑等。

接下来就是找到APP支付的入口，可以通过搜索success、pay、paid等关键字符串来找到相关文件。

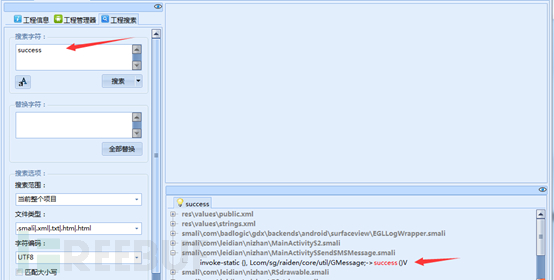
点进这个文件进行查看，我们可以看到一些与支付相关的字符串，猜测这里可能就是支付函数的入口，至于到底是不是，我们接着看下面。

这些smali语句可能看着晦涩难懂，没关系，我们可以通过AndroidKiller将其转化为我们熟悉的java代码。

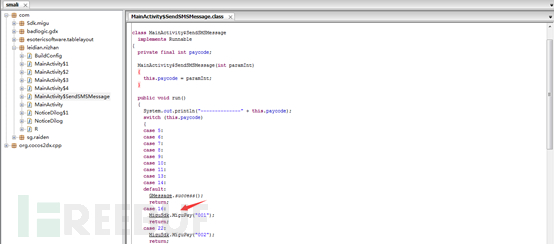
这里是一个switch语句，可能是对支付功能做的一些判断。我们可以看到这里有个MiguPay函数，这个函数到底是干什么的呢？点击MiguSdk类，可以跳转到MiguSdk类。

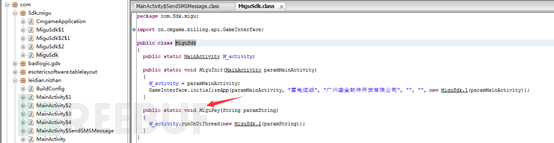
我们可以看到该方法里调用了runOnUiThread方法，其参数中有涉及另外一个类MiguSdk.2，跟着这个方法继续跳转下去。

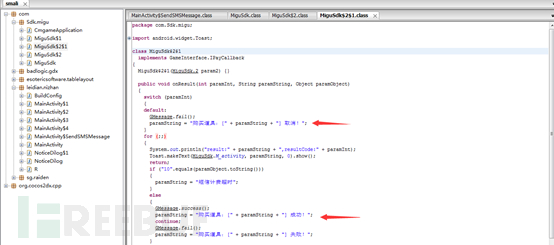
令人惊喜的一幕出现了，我们可以看到“购买道具”“成功”等字符串，到这里差不多就可以肯定这里就是与支付相关的方法了！好了，我们又跳转到之前switch判断的函数。

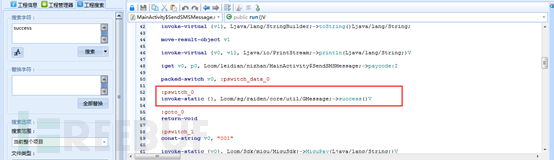
之前我们看到，当调用GMessage.success()时，就是说明购买成功。而这里的:pswitch_0语句就是发送的GMessage.success()。这就意味着，如果所有的判断语句都和pswitch_0里执行的一样，那么是不是所有的条件都能购买成功呢？我们试试，将所有的:pswitch_x全部改为pswitch_0。

用AndroidKiller对该APP进行打包签名，安装测试！

安装失败！提示签名校验不通过！看来该APP进行了签名校验，所谓的签名校验就是为了防止自己的应用被反编译后重新打包。那么有没有方法进行绕过呢？当然有！其实签名校验一般写在native层so文件里，或者是java层。通过搜索SignKey、Signature等关键字符串，一般可以找到签名校验的入口。以下文件就是判断签名的so文件里的相关函数，利用工具IDA转换为C语言的伪代码。

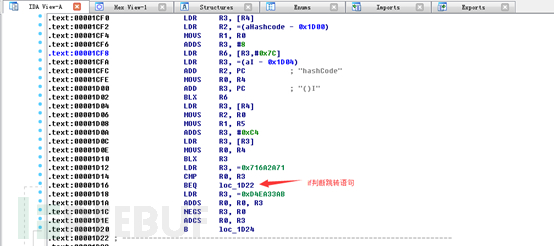
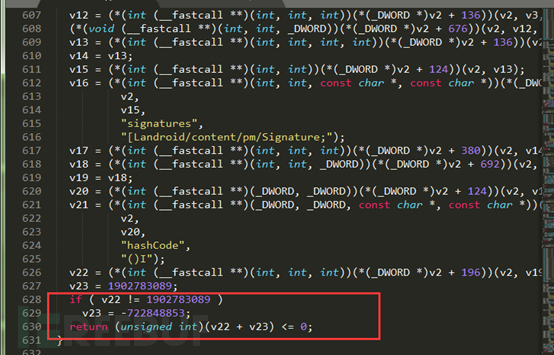
从上图可以看出，最后做了个if语句的判断，那么我们直接用十六进制编辑器将return语句直接改为return true。最后再次编译打包该APP，ok！破解成功！

思考：开发一个有商用价值的APP，无疑是需要大量的精力的，如果APP能被轻易破解，那带来的损失肯定是让人无法接受的。因此对于APP的安全防护显得至关重要。关于APP逆向的安全机制，一般有以下几种：

1、  代码混淆：对发布出去的程序进行重新组织和处理，使得处理后的代码与处理前代码完成相同的功能，而混淆后的代码很难被反编译，即使反编译成功也很难得出程序的真正语义。

2、  签名校验：比较用来签名app的证书的hash与我们写死在其中的hash是否一致。

3、  加壳处理：在二进制的程序中植入一段代码，在运行的时候优先取得程序的控制权，做一些额外的工作。