L2范数归一化概念和优势

1 归一化处理

       归一化是一种数理统计中常用的数据预处理手段，在机器学习中归一化通常将数据向量每个维度的数据映射到(0,1)或(-1,1)之间的区间或者将数据向量的某个范数映射为1，归一化好处有两个：

       (1) 消除数据单位的影响：其一可以将有单位的数据转为无单位的标准数据，如成年人的身高150-200cm、成年人体重50-90Kg，身高的单位是厘米而体重的单位是千克，不同维度的数据单位不一样，造成原始数据不能直接代入机器学习中进行处理，所以这些数据经过特定方法统一都映射到(0,1)这个区间,这样所有数据的取值范围都在同一个区间里的。

       (2) 可提深度学习模型收敛速度: 如果不进行归一化处理，假设深度学习模型接受的输入向量只有两个维度x1和x2，其中X1取值为0-2000，x2取值为0-3。这样数据在进行梯度下降计算时梯度时对应一个很扁的椭圆形，很容易在垂直等高线的方向上走大量的之字形路线，是的迭代计算量大且迭代的次数多，造成深度学习模型收敛慢。

2 L2范数归一化的概念

       L2范数归一化处理操作是对向量X的每个维度数据x1, x2, …, xn都除以||x||2得到一个新向量，即
\[{{\bf{X}}_2} = \left( {\frac{{{x_1}}}{{{{\left\| {\bf{x}} \right\|}_2}}},\frac{{{x_2}}}{{{{\left\| {\bf{x}} \right\|}_2}}}, \cdots ,\frac{{{x_n}}}{{{{\left\| {\bf{x}} \right\|}_2}}}} \right) = \left( {\frac{{{x_1}}}{{\sqrt {x_1^2 + x_2^2 + \cdots + x_n^2} }},\frac{{{x_2}}}{{\sqrt {x_1^2 + x_2^2 + \cdots + x_n^2} }}, \cdots ,\frac{{{x_n}}}{{\sqrt {x_1^2 + x_2^2 + \cdots + x_n^2} }}} \right)\]

       若向量A = (2, 3, 6)，易得向量X的L2范数为
\[{\left\| {\bf{A}} \right\|_2} = \sqrt {{2^2} + {3^2} + {6^2}} = \sqrt {4 + 9 + 36} = \sqrt {49} = 7\]

       所以向量A的L2范数归一化后得到向量为
\[{{\bf{A}}_2} = \left( {\frac{2}{7},\frac{3}{7},\frac{6}{7}} \right)\]

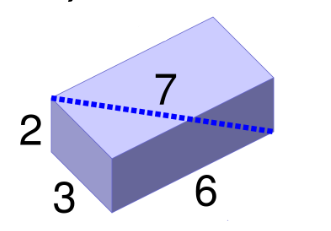
图1 L2范数可以看作是向量的长度

3 L2范数归一化的优势

       L2范数有一大优势：经过L2范数归一化后，一组向量的欧式距离和它们的余弦相似度可以等价

       一个向量X经过L2范数归一化得到向量X2，同时另一个向量Y经过L2范数归一化得到向量Y2。此时X2和Y2的欧式距离和余弦相似度是等价的，下面先给出严格的数学证明。

       假设向量X = (x1, x2, …, xn)，向量Y = (y1, y2, …, yn)， X2和Y2的欧式距离是
\[\begin{array}{l}
D\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right) = \sqrt {{{\left( {\frac{{{x_1}}}{{{{\left\| {\bf{X}} \right\|}_2}}} - \frac{{{y_1}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^2} + {{\left( {\frac{{{x_2}}}{{{{\left\| {\bf{X}} \right\|}_2}}} - \frac{{{y_2}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^2} + \cdots + {{\left( {\frac{{{x_n}}}{{{{\left\| {\bf{X}} \right\|}_2}}} - \frac{{{y_n}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^2}} \\
\quad \quad \quad \quad \quad \;\;\; = \sqrt {\left( {\frac{{\bf{X}}}{{{{\left\| {\bf{X}} \right\|}_2}}} - \frac{{\bf{Y}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right){{\left( {\frac{{\bf{X}}}{{{{\left\| {\bf{X}} \right\|}_2}}} - \frac{{\bf{Y}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^T}} \\
\quad \quad \quad \quad \quad \;\;\; = \sqrt {\frac{{{\bf{X}}{{\bf{X}}^T}}}{{\left\| {\bf{X}} \right\|_2^2}} - \frac{{{\bf{X}}{{\bf{Y}}^T}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}} - \frac{{{\bf{Y}}{{\bf{X}}^T}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}} + \frac{{{\bf{Y}}{{\bf{Y}}^T}}}{{\left\| {\bf{Y}} \right\|_2^2}}} \\
\quad \quad \quad \quad \quad \;\;\; = \sqrt {\frac{{{\bf{X}}{{\bf{X}}^T}}}{{{\bf{X}}{{\bf{X}}^T}}} - \frac{{2{\bf{X}}{{\bf{Y}}^T}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}} + \frac{{{\bf{Y}}{{\bf{Y}}^T}}}{{{\bf{Y}}{{\bf{Y}}^T}}}} \\
\quad \quad \quad \quad \quad \;\;\; = \sqrt {2 - 2\frac{{{\bf{X}}{{\bf{Y}}^T}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}}} \\
\end{array}\]

       X2和Y2的余弦相似度为
\[\begin{array}{l}
Sim\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right) = \frac{{\frac{{{x_1}}}{{{{\left\| {\bf{X}} \right\|}_2}}} \cdot \frac{{{y_1}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}{\rm{ + }}\frac{{{x_{\rm{2}}}}}{{{{\left\| {\bf{X}} \right\|}_2}}} \cdot \frac{{{y_{\rm{2}}}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}{\rm{ + }} \cdots {\rm{ + }}\frac{{{x_n}}}{{{{\left\| {\bf{X}} \right\|}_2}}} \cdot \frac{{{y_n}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}}}{{\sqrt {{{\left( {\frac{{{x_1}}}{{{{\left\| {\bf{X}} \right\|}_2}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {\frac{{{x_{\rm{2}}}}}{{{{\left\| {\bf{X}} \right\|}_2}}}} \right)}^{\rm{2}}}{\rm{ + }} \cdots {{\left( {\frac{{{x_{\rm{n}}}}}{{{{\left\| {\bf{X}} \right\|}_2}}}} \right)}^{\rm{2}}}} \cdot \sqrt {{{\left( {\frac{{{y_1}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^{\rm{2}}}{\rm{ + }}{{\left( {\frac{{{y_{\rm{2}}}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^{\rm{2}}}{\rm{ + }} \cdots {\rm{ + }}{{\left( {\frac{{{y_n}}}{{{{\left\| {\bf{Y}} \right\|}_2}}}} \right)}^{\rm{2}}}} }} \\
\quad \quad \quad \quad \quad \;\;\; = \frac{{\frac{{{x_1}{y_1} + {x_2}{y_2} + \cdots + {x_n}{y_n}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}}}}{{\sqrt {\frac{{x_1^2 + x_2^2 + \cdots + x_n^2}}{{\left\| {\bf{X}} \right\|_2^2}}} \cdot \sqrt {\frac{{y_1^2 + y_2^2 + \cdots y_n^2}}{{\left\| {\bf{Y}} \right\|_2^2}}} }} \\
\quad \quad \quad \quad \quad \;\;\; = \frac{{\frac{{{x_1}{y_1} + {x_2}{y_2} + \cdots + {x_n}{y_n}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}}}}{{\sqrt {\frac{{x_1^2 + x_2^2 + \cdots + x_n^2}}{{x_1^2 + x_2^2 + \cdots + x_n^2}}} \cdot \sqrt {\frac{{y_1^2 + y_2^2 + \cdots y_n^2}}{{y_1^2 + y_2^2 + \cdots y_n^2}}} }} \\
\quad \quad \quad \quad \quad \;\;\; = \frac{{{x_1}{y_1} + {x_2}{y_2} + \cdots + {x_n}{y_n}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}} \\
\quad \quad \quad \quad \quad \;\;\; = \frac{{{\bf{X}}{{\bf{Y}}^T}}}{{{{\left\| {\bf{X}} \right\|}_2}{{\left\| {\bf{Y}} \right\|}_2}}} \\
\end{array}\]
       结合两个表达式易得
\[D\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right) = \sqrt {2 - 2sim\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right)} \]

       即L2范数归一化处理后两个向量欧式距离等于2减去2倍余弦相似度的算术平方根。如果你被上面令人昏头转向的数学公式搞晕，而不想看的话，这里还有一种仅需要中学知识的更简单证明方法证明两者的等价性:

       假设一组二维数据，设经过L2范数归一化后向量X2 为 (p1, p2)，向量Y2 为 (q1, q2)。向量X2是原点(0,0) 指向点P(p1,p2)的有向线段，向量Y2是原点(0,0)指向点Q(q1, q2)的有向线段。易得

       X2和Y2的欧式距离为线段PQ长度

       X2和Y2的余弦相似度为∠POQ的余弦值

       根据余弦定理易得

\[\cos \angle POQ = \frac{{O{P^2} + O{Q^2} - P{Q^2}}}{{2 \cdot OP \cdot OQ}}\]

       因为L2范数归一化向量的长度都是1，因为L2范数归一化向量的长度都是1，那么向量对应的点肯定都在单位圆上，所以OP=OQ=1

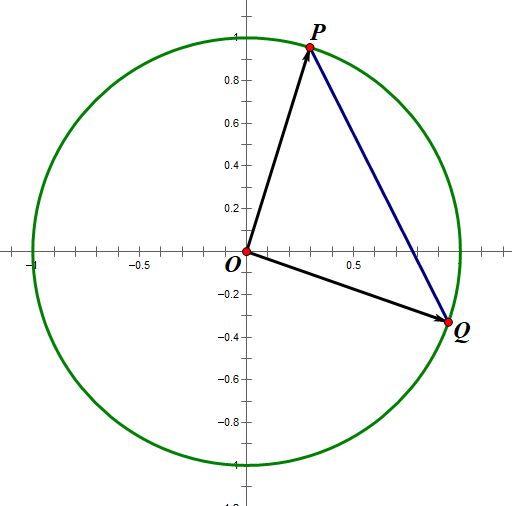
图2 L2范数归一化后向量对应的点都在单位圆上

       因此
\[\cos \angle POQ = \frac{{{1^2} + {1^2} - P{Q^2}}}{2} = \frac{{2 - P{Q^2}}}{2}\]

       即
\[sim\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right) = \frac{{2 - D{{\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right)}^2}}}{2} \Rightarrow D\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right) = \sqrt {2 - 2sim\left( {{{\bf{X}}_{\rm{2}}},{{\bf{Y}}_{\rm{2}}}} \right)} \]

       因此经L2范数归一化后，一组向量的欧式距离和它们的余弦相似度可等价。这一大优势是当你算得一组经过L2范数归一化后的向量的欧式距离后，又想计算它们的余弦相似度，可以根据公式在O(1)时间内直接计算得到；反过来也一样。

       另外，在一些机器学习处理包中，只有欧式距离计算没有余弦相似度计算，如Sklearn的Kmeans聚类包，这个包只能处理欧式距离计算的数据聚类。

       而在NLP领域，许多词语或文档的相似度定义为数据向量的余弦相似度，如果直接调用Sklearn的Kmeans聚类包则不能进行聚类处理。因此需要将词语对象的词向量或者文档对应的文本向量进行L2范数归一化处理。因为在L2范数归一化处理后的欧式距离和余弦相似度是等价的，所以此时可以放心大胆用Sklearn的Kmeans进行聚类处理。