长乐国庆集训Day1

T1 统计数字

题目

【题目描述】

设 S(N ) 表示 N 的各位数字之和，如 S(484) = 4+8+4 = 16， S(22) = 2+2 = 4。

如果一个正整数满足 S(x*x) = S(x) *S(x)，我们称之为 Rabbit N umber。比方说，22 就是一个 Rabbit N umber，因为 S(484) = S(22) *S(22)。

现在，给出一个区间 [L, R]，求在该区间内的 Rabbit N umber 的个数。

【输入格式】

输入仅一行，为空格隔开的两个数 L 和 R。

【输出格式】

输出仅一行一个整数，表示所求 Rabbit N umber 的个数。

【输入样例】

【输出样例】

【数据规模】

1 <= L <= R <= 10^9

解析

看完题目第一反应：从L枚举到R，依次判断每个数是不是Rabbit N umber。然而数据规模是10⁹，显然超时。

不过没事，打完暴力后，随便试一些数字，看看有没有什么规律。

1~1000内的Rabbit N umber如下：

不难发现，无论是哪一位上，都没有大于3的数字（更大的范围内也是，可以自己试试），至于为什么，这里便不给出详细证明了（因为本蒟蒻不会）。

所以便有了剪纸：任何位上有大于3的数字就跳过。

于是便有了两种做法：

dfs+剪纸
打表+二分

打表这里就不说了（太麻烦），这里来讲dfs做法：

dfs(int temp):temp可以理解为当前数是由temp+一个新的个位数组成的数，具体看代码就懂了。

从temp=0开始搜，每次dfs函数里处理个位为0 1 2 3的数，满足条件且在L~R的范围内就累加个数，

处理完后，如果数字小于等于R/10的话，就dfs(x)（即还可以增加位数）。

最后输出总个数就好了，别忘了开long long，至于S(x)，直接模拟就好了。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

long long read()

{

    long long num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

long long l,r,ans;

int S(long long x)

{

    int n=;

    while(x>)

    {

        n+=x%;

        x/=;

    }

    return n;

}

void dfs(int temp)

{

    for(int i=;i<=;i++)

    {

        long long x=temp*+i;

        int s=S(x);

        if(x==||S(x*x)!=s*s) continue;

        if(l<=x&&r>=x) ans++;

        if(x<=r/) dfs(x);

    }

}

int main()

{

    //freopen("rabbit.in","r",stdin);

    //freopen("rabbit.out","w",stdout);

    l=read(),r=read();

    dfs();

    cout<<ans;

    return ;

}

T2 数边方案

题目

【题目描述】

给你一张有n个点m条边的无向连通图，每条边有边权，设disa_i表示这张图中点i到点1的最短距离。

现在要求你在这张图中删去m-(n-1)条边，使得这张图变成一棵树，设disb_i表示这棵树中点i到点1的最短距离。现在请你求出，有多少种删边方案，使得对于任意的i，都有disa_i=disb_i。

【输入格式】

第一行包含两个正整数n,m，表示无向连通图的点数和边数。

接下来有m行，每行有3个正整数u,v,w，表示点u和点v之间有一条边权为w的无向边。

数据保证无重边、无自环。

【输出格式】

输出一行一个整数，表示满足条件的方案数对2147483647取模的结果。

【输入样例】

【输出样例】

【数据规模】

解析

据说有个叫最短路图的东西，就是把原图中满足dis(u)+w=dis(v)的边(u,v,w)保留下来构成的子图。

本题中，边权一定为正整数，所以最短路图是一个有向无环图，答案只需枚举有向无环图中生成树的数量即可，然而仍然过不了。

事实上，在构造最短路图的过程中，就是在给每个点选一个父亲，而可选父亲总数就是这个点的入度，显然答案为入度之积。

具体实现是用最短路，本蒟蒻采用的是Dijkstra。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

#include <queue>

using namespace std;

priority_queue<pair<int,int> > q;

const int N=,M=;

const long long mod=;

int n,m,head[N],ver[M],edge[M],from[M],tot,next[M],d[N],deg[N];

long long ans=;

bool v[N];

void add(int x,int y,int z)

{

    ver[++tot]=y,edge[tot]=z,from[tot]=x,next[tot]=head[x],head[x]=tot;

}

void dijkstra()

{

    memset(d,0x7f7f7f7f,sizeof(d));

    memset(v,false,sizeof(v));

    d[]=;

    q.push(make_pair(,));

    while(q.size())

    {

        int x=q.top().second;

        q.pop();

        if(v[x]) continue;

        v[x]=;

        for(int i=head[x];i;i=next[i])

        {

            int y=ver[i],z=edge[i];

            if(d[y]>d[x]+z)

            {

                d[y]=d[x]+z;

                q.push(make_pair(-d[y],y));

            }

        }

    }

    for(int i=;i<=tot;i++)

    {

        int x=from[i],y=ver[i],z=edge[i];

        if(d[x]+z==d[y]) deg[y]++;

    }

    for(int i=;i<=n;i++)

        if(deg[i]) ans=(1LL*ans*deg[i])%mod;

}

int main()

{

    cin>>n>>m;

    for(int i=;i<=m;i++)

    {

        int x,y,z;

        cin>>x>>y>>z;

        add(x,y,z);

        add(y,x,z);

    }

    dijkstra();

    cout<<ans;

    return ;

}

T3 开根号

题目

【题目描述】

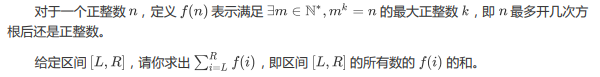
【输入格式】

输入包含多组数据。每组数据包含一行两个正整数L,R。

文件以0 0结尾（结尾不需要输出）。

【输出格式】

对于每组数据，输出一行表示答案。保证答案在[0,2⁶³)范围内。

【样例输入】

【样例输出】

【数据规模】

解析

可怕的数论题~~~

先把区间求和用前缀和表示，所以只需求[1,n]的答案。

依次求每个数的f(i)很麻烦，考虑求[1,n]中f(i)=k的个数，其个数用g(k)表示。

用p(k)表示[1,n]中开k次方还是正整数的数的个数，可以得到p(k)=n^1/k(向下取整)。

则。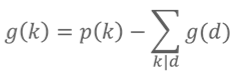

所以用递推推出答案就可以了。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

const double eps=1e-;

long long l,r,f[];

long long solve(long long x)

{

    if(x<) return ;

    int num=;

    for(int i=;i>=;i--)

    {

        f[i]=(long long)(pow(x,(double)1.0/i)+eps)-;

        for(int j=i+i;j<=;j+=i) f[i]-=f[j];

        num+=f[i]*(i-);

    }

    return num+x;

}

int main()

{

    cin>>l>>r;

    while(l!=&&r!=)

    {

        cout<<solve(r)-solve(l-)<<endl;

        cin>>l>>r;

    }

    return ;

}

T4 旅行

题目

【题目描述】

【输入格式】

第一行包含两个非负整数n,k，含义如【题目描述】所述。

接下来n-1行，每行三个正整数u,v,w，表示u,v之间有一条边权为w的边。

【输出格式】

输出一行一个整数，表示答案。保证存在合法解。

【输入样例】

【输出样例】

【数据规模】

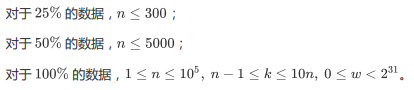
解析

不难发现：

dis(u,v)=dis(u,1)+dis(v,1)。
如果经过的边数为奇数，那么必定有一个点的深度为奇数，另一个点的深度为偶数。

所以将所有点按深度的奇偶来分类，于是就有了两个序列a，b，只需求a_i+b_i的第k小值即可。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

#include <queue>

using namespace std;

const int N=;

struct node

{

    long long v;

    int p;

    node(long long a,int b):v(a),p(b){}

    bool operator < (const node &a) const

    {

        return v>a.v;

    }

};

priority_queue<node> q;

int head[N],ver[N<<],edge[N<<],next[N<<],tot;

long long dis[N],deep[N],a[N],b[N],cnta,cntb;

void add(int x,int y,int z)

{

    ver[++tot]=y,edge[tot]=z,next[tot]=head[x],head[x]=tot;

}

void dfs(int x,int fa)

{

    for(int i=head[x];i;i=next[i])

    {

        int y=ver[i],z=edge[i];

        if(y==fa) continue;

        dis[y]=-dis[x]+z,deep[y]=deep[x]+;

        dfs(y,x);

    }

}

int main()

{

    int n,k;

    cin>>n>>k;

    for(int i=;i<=n-;i++)

    {

        int x,y,z;

        cin>>x>>y>>z;

        add(x,y,z);

        add(y,x,z);

    }

    dfs(,);

    for(int i=;i<=n;i++)

        if(deep[i]&) a[++cnta]=dis[i];

        else b[++cntb]=dis[i];

    sort(b+,b+cntb+);

    for(int i=;i<=cnta;i++) q.push(node(a[i]+b[],i));

    for(int i=;i<=cnta;i++) head[i]=;

    while(k>)

    {

        node t=q.top();

        q.pop();

        if((++head[t.p])<=cntb) q.push(node(a[t.p]+b[head[t.p]],t.p));

        k--;

    }

    cout<<q.top().v;

    return ;

}