trie树（前缀树）详解——PHP代码实现

trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

一、Tire树的基本性质

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
• 每个节点的所有子节点包含的字符都不相同。

Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起，比如我们有[b,abc,abd,bcd,abcd,efg,hii ]这个字符串集合，可以将其构建成下面这棵 Trie 树：

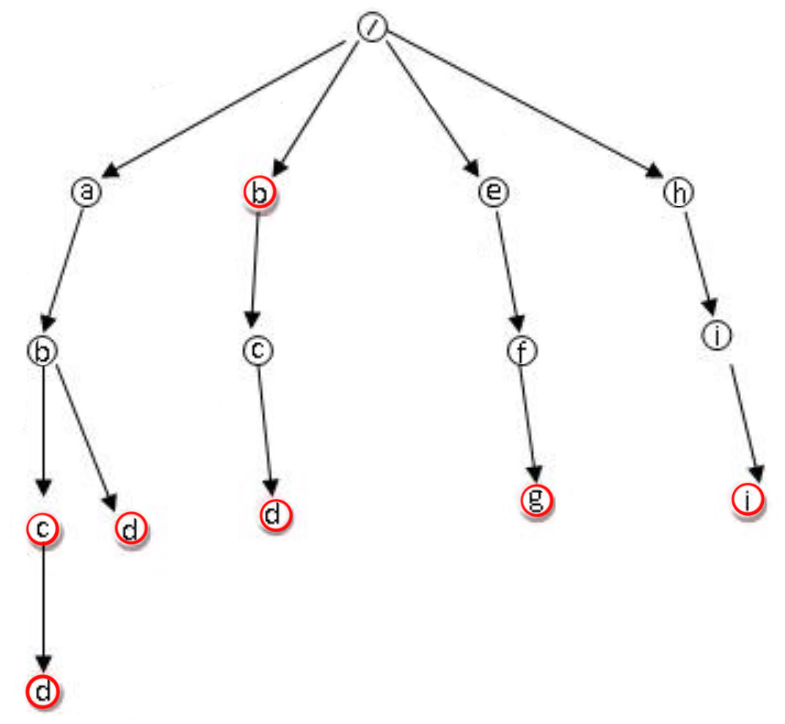
每个节点表示一个字符串中的字符，从根节点到红色节点的一条路径表示一个字符串（红色节点表示是某个单词的结束字符，但不一定都是叶子节点）。这样，我们就可以通过遍历这棵树来检索是否存在待匹配的字符串了

二、如何实现Tire树

Tire主要包含两个操作，一个是将字符串集合构造成 Trie 树。这个过程分解开来的话，就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。

Trie 树是个多叉树，在这里用数组来存储一个节点的所有子结点。

Trie树节点类，PHP代码实现：

 <?php
 /**
  * TrieNode.php
  * Created on 2019/4/29 14:53
  * Created by Wilin
  */

 class TrieNode
 {
     public $data;
     public $children = [];
     public $isEndingChar = false;

     public function __construct($data)
     {
         $this->data = $data;
     }
 }

Trie树，PHP代码实现：

 <?php
 /**
  * Tire.php
  * Created on 2019/4/29 14:57
  * Created by Wilin
  */

 include "TrieNode.php";

 class Tire {
     private $root;

     public function __construct() {
         $this->root = new TrieNode('/'); //根节点
     }

     public function getRoot() {
         return $this->root;
     }

     public function insert($text) {
         $p = $this->root;
         for ($i = 0; $i < mb_strlen($text); $i++) {
             $index = $data = $text[$i];

             if (empty($p->children[$index])) {
                 $newNode = new TrieNode($data);
                 $p->children[$index] = $newNode;
             }
             $p = $p->children[$index];
         }
         $p->isEndingChar = true;
     }

     public function find($pattern) {
         $p = $this->root;
         for ($i = 0; $i < mb_strlen($pattern); $i++) {
             $index = $data = $pattern[$i];

             if (empty($p->children[$index])) {
                 return false;
             }
             $p = $p->children[$index];
         }
         if ($p->isEndingChar == false) {
             return false;
         }
         return true;
     }
 }

 $trie = new Tire();
 $strings = ['b','abc','abd','bcd','abcd','efg','hii'];
 foreach ($strings as $str) {
     $trie->insert($str);
 }
 if ($trie->find('bcd')) {
     print "包含这个字符串\n";
 } else {
     print "不包含这个字符串\n";
 }
 print_r($trie->getRoot());

打印结果如下：

E:\www\tree\3>php Tire.php
包含这个字符串
TrieNode Object
(
    [data] => /
    [children] => Array
        (
            [b] => TrieNode Object
                (
                    [data] => b
                    [children] => Array
                        (
                            [c] => TrieNode Object
                                (
                                    [data] => c
                                    [children] => Array
                                        (
                                            [d] => TrieNode Object
                                                (
                                                    [data] => d
                                                    [children] => Array
                                                        (
                                                        )

                                                    [isEndingChar] => 1
                                                )

                                        )

                                    [isEndingChar] =>
                                )

                        )

                    [isEndingChar] => 1
                )

            [a] => TrieNode Object
                (
                    [data] => a
                    [children] => Array
                        (
                            [b] => TrieNode Object
                                (
                                    [data] => b
                                    [children] => Array
                                        (
                                            [c] => TrieNode Object
                                                (
                                                    [data] => c
                                                    [children] => Array
                                                        (
                                                            [d] => TrieNode Object
                                                                (
                                                                    [data] => d
                                                                    [children] => Array
                                                                        (
                                                                        )

                                                                    [isEndingChar] => 1
                                                                )

                                                        )

                                                    [isEndingChar] => 1
                                                )

                                            [d] => TrieNode Object
                                                (
                                                    [data] => d
                                                    [children] => Array
                                                        (
                                                        )

                                                    [isEndingChar] => 1
                                                )

                                        )

                                    [isEndingChar] =>
                                )

                        )

                    [isEndingChar] =>
                )

            [e] => TrieNode Object
                (
                    [data] => e
                    [children] => Array
                        (
                            [f] => TrieNode Object
                                (
                                    [data] => f
                                    [children] => Array
                                        (
                                            [g] => TrieNode Object
                                                (
                                                    [data] => g
                                                    [children] => Array
                                                        (
                                                        )

                                                    [isEndingChar] => 1
                                                )

                                        )

                                    [isEndingChar] =>
                                )

                        )

                    [isEndingChar] =>
                )

            [h] => TrieNode Object
                (
                    [data] => h
                    [children] => Array
                        (
                            [i] => TrieNode Object
                                (
                                    [data] => i
                                    [children] => Array
                                        (
                                            [i] => TrieNode Object
                                                (
                                                    [data] => i
                                                    [children] => Array
                                                        (
                                                        )

                                                    [isEndingChar] => 1
                                                )

                                        )

                                    [isEndingChar] =>
                                )

                        )

                    [isEndingChar] =>
                )

        )

    [isEndingChar] =>
)

参考资料：https://www.cnblogs.com/luosongchao/p/3239521.html，https://articles.zsxq.com/id_qa0npqvszcmx.html