hiho#1033 : 交错和

描述

给定一个数 x，设它十进制展从高位到低位上的数位依次是 a0, a1, ..., an - 1，定义交错和函数：

f(x) = a0 - a1 + a2 - ... + ( - 1)n - 1an - 1

例如：

f(3214567) = 3 - 2 + 1 - 4 + 5 - 6 + 7 = 4

给定

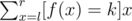
输入

输入数据仅一行包含三个整数，l, r, k(0 ≤ l ≤ r ≤ 1018, |k| ≤ 100)。

输出

输出一行一个整数表示结果，考虑到答案可能很大，输出结果模 109 + 7。

提示

对于样例 ，满足条件的数有 110 和 121，所以结果是 231 = 110 + 121。

更多样例：

Input

4344 3214567 3

Output

611668829

Input

404491953 1587197241 1

Output

323937411

Input

60296763086567224 193422344885593844 10

Output

608746132

Input

100 121 -1

Output

120

样例输入

100 121 0

样例输出

231

显然是很裸的数位DP，但写起来就有些MD了。
设f[len][x][k]表示长度为len，首位为x，交错和为k的数之和，g[len][x][k]表示长度为len，首位为x，交错和为k的数的个数。
然后转移比较简单自己歪歪或看我的code，询问时注意：rep(i,0,len-2) rep(j,1,9) (res+=f[i][j][k+200])%=MOD;    MD调了2h。

#include<cstdio>
#include<cctype>
#include<queue>
#include<cmath>
#include<cstring>
#include<algorithm>
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define dwn(i,s,t) for(int i=s;i>=t;i--)
#define ren for(int i=first[x];i!=-1;i=next[i])
using namespace std;
inline int read() {
    int x=,f=;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-;
    for(;isdigit(c);c=getchar()) x=x*+c-'';
    return x*f;
}
typedef long long ll;
ll f[][][],g[][][],xp[];
const int MOD=;
void init() {
    rep(i,,) f[][i][i+]=i,g[][i][i+]=;
    xp[]=;
    rep(len,,) {
        xp[len]=(xp[len-]*)%MOD;
        rep(k,-,) rep(x,,) rep(y,,) if(x-k>=-&&x-k<=) {
            f[len][x][x-k+]+=f[len-][y][k+]+(g[len-][y][k+]*(xp[len]*x))%MOD;
            (g[len][x][x-k+]+=g[len-][y][k+])%=MOD;
            f[len][x][x-k+]%=MOD;
        }
    }
}
int bit[],len,k;
ll cal(ll x) {
    if(x<=) return ;
    ll res=,cur2=;int cur=,c=;len=;
    while(x) bit[len++]=x%,x/=;
    rep(i,,len-) rep(j,,) (res+=f[i][j][k+])%=MOD;
    dwn(i,len-,) {
        c^=;
        rep(j,,bit[i]-) {
            if(!j&&i==len-) continue;
            if(c) (res+=f[i][j][k-cur+]+g[i][j][k-cur+]*cur2)%=MOD;
            else (res+=f[i][j][cur-k+]+g[i][j][cur-k+]*cur2)%=MOD;
        }
        if(c) cur+=bit[i];
        else cur-=bit[i];
        (cur2+=bit[i]*xp[i])%=MOD;
    }
    return res;
}
int main() {
    init();
    ll l,r;
    scanf("%lld%lld",&l,&r);k=read();
    printf("%lld\n",(cal(r+)-cal(l)+MOD)%MOD);
    return ;
}