回文串---Hotaru's problem

HDU   5371

Description

Hotaru Ichijou recently is addicated to math problems. Now she is playing with N-sequence. 
Let's define N-sequence, which is composed with three parts and satisfied with the following condition: 
1. the first part is the same as the thrid part, 
2. the first part and the second part are symmetrical. 
for example, the sequence 2,3,4,4,3,2,2,3,4 is a N-sequence, which the first part 2,3,4 is the same as the thrid part 2,3,4, the first part 2,3,4 and the second part 4,3,2 are symmetrical.

Give you n positive intergers, your task is to find the largest continuous sub-sequence, which is N-sequence.

 

Input

There are multiple test cases. The first line of input contains an integer T（T<=20）, indicating the number of test cases.

For each test case:

the first line of input contains a positive integer N（1<=N<=100000）, the length of a given sequence

the second line includes N non-negative integers ,each interger is no larger than  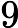, descripting a sequence. 

 

Output

Each case contains only one line. Each line should start with “Case #i: ”,with i implying the case number, followed by a integer, the largest length of N-sequence.

We guarantee that the sum of all answers is less than 800000.

 

Sample Input

1
10
2 3 4 4 3 2 2 3 4 4

 

Sample Output

Case #1: 9

 

Source

2015 Multi-University Training Contest 7

 

题意：给一个长为n的序列，求最长连续子序列的长度，这个子序列满足这样的特点：这个子序列由前到后分为长度相等的三部分，第一部分与第二部分对称，第一部分与第三部分相同;

 

思路：先利用回文串算法求出以第i个字符为中心的最大回文长度，然后在这个回文串的最右边的字符出开始判断，如果以这个字符为中心的回文串长度小于前面那个字符的回文串长度，这个比较的字符左移，再次比较，找到以第i个字符为中心的最大长度好，将length个字符遍历一遍就可找到最大的长度。直接这样求解会超时，可以在右边的那个比较的字符向左移动的过程中加上一些判断条件，减少无用的计算。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N=;
int p[*N];
int s[*N],str[*N];
int n;

void kp()
{
    int mx=;
    int id;
    for(int i=;i<n;i++)
    {
        if(mx>i)
            p[i]=min(p[*id-i],p[id]+id-i);
        else
            p[i]=;
        for( ;i+p[i]<n;)
        {
            if(str[i+p[i]]==str[i-p[i]])
            {
                if(str[i+p[i]]==) p[i]++;
                else
                {
                    p[i]+=;
                }
            }
            else break;
        }
        if(p[i]+i>mx)
        {
            mx=p[i]+i;
            id=i;
        }
    }
}

void init()
{
    str[]=;
    str[]=;
    for(int i=; i<n; i++)
    {
        str[i*+]=s[i];
        str[i*+]=;
    }
    n=n*+;
}

int main()
{
    int T,Case=;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=;i<n;i++)
        scanf("%d",&s[i]);
        if(n<)
        {
            printf("%d",);
        }
        init();
        kp();
        ///cout<<p[11]<<"++"<<p[15]<<endl;
        int sum=0;
        for(int i=;i<=n-;i=i+)
        {
            if(p[i]-<=sum/*) continue;
            int t=p[i];
            for(int j=t-;j>=;j=j-)
            {
                if(j<=sum/*) break;
                if(i+j>n) continue;///可能这儿超时；
                if(p[i+j]->=j)
                {
                    sum=max(sum,j/*);
                    break;
                }
            }
        }
        printf("Case #%d: %d\n",Case++,sum);
    }
    return ;
}