Python 汉诺塔

在汉诺塔游戏中，有三个分别命名为A、B、C得塔座，几个大小各不相同，从小到大一次编号得圆盘，每个原盘中间有一个小孔。最初，所有得圆盘都在A塔座上，其中最大得圆盘在最下面，然后是第二大，以此类推.

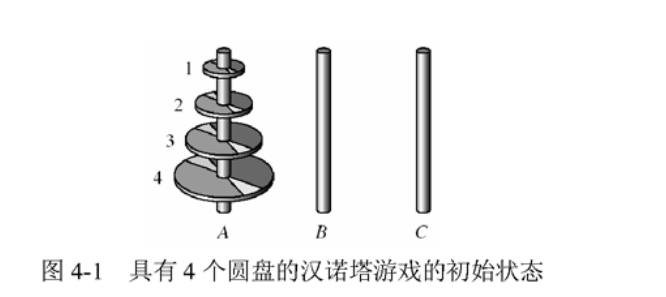
　游戏的目的是将所有的圆盘从塔座A移动到塔座B;塔座C用来防止临时圆盘,游戏的规则如下：

　　　　1、一次只能移动一个圆盘。

　　　　2、任何时候都不能将一个较大的圆盘压在较小的圆盘上面。

　　　　3、除了第二条限制,任何塔座的最上面的圆盘都可以移动到其他塔座上。

　汉诺塔问题解决思想：

　　　　在解决汉诺塔问题时，事实上，我们不是罪关心圆盘1开始应该挪到哪个塔座上，而是关心最下面的圆盘4。当然,我们不能直接移动圆盘4，但是圆盘4最终将从塔座A移动到塔座B。按照游戏规则，在移动圆盘4之前的情况一定如下图

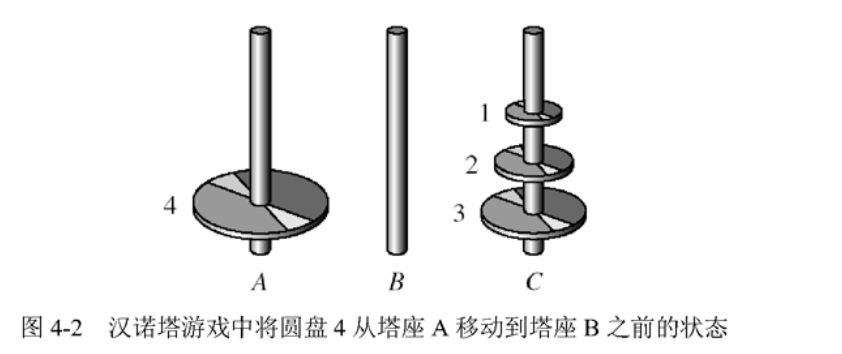
　　我们仍将分析，如何将前三个圆盘从A移动到C，然后圆盘4从A移动到B，前三个圆盘从C再移动到B。

　　但是上面的步骤可以重复利用!例如将三个圆盘从A移动到C，那么应该先将前两个圆盘从A移动到B，然后将圆盘3从A移动到C，最后将前两个圆盘从B移动到C。

　　持续简化这个问题，最终我们将只需要处理一个圆盘从一个塔座移动到另一个塔座的问题。

总而言之，就是将一座塔移动到另一座塔上，且移动的过程中大的圆盘不能在小的圆盘上面。

#codiing = utf-8

def hanoi(n,a,b,c):   #n = 圆盘数 ； a,b,c为三棵柱子（即起点、缓冲区、终点）
    if n == 1:
        print(a, '-->', c)
    else:
        hanoi(n - 1, a, c, b)
        print(a, '-->', c)
        hanoi(n - 1, b, a, c)

if __name__ == '__main__':
    hanoi(4,'A','B','C')     #输出把所有盘子从A借助B移动到C的方法