[leecode]---11.container with most water

description:

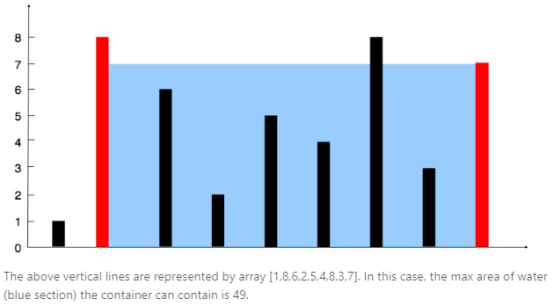
Input: [1,8,6,2,5,4,8,3,7]Output: 49

思路1：

　　从(1,a1)开始向后算面积，需要两层n循环，时间复杂度n²

思路2：

　　找出数组中最大的数，将其与次大，第三大数求面积，依次类推，也需要两层循环，还需要额外排序，时间复杂度n²

　　因为找出最大数并且并不知道输入数据的规律（有可能很杂乱），所以每个都有必要算，采取思路1.

　　代码实现如下：

class Solution {
    public int maxArea(int[] height) {
        int max = 0;
        for(int i = 0; i < height.length; i++){
            int mid = maxSpare(height, i);
            max = max >= mid ? max : mid;
        }
        return max;
    }
    // 从index = start开始向后对每一对求面积
    private int maxSpare(int[] height, int start){
        int maxArea = 0;
        for(int i = start + 1; i < height.length; i++){
            int area = countArea(height[start], height[i], i - start);
            maxArea = maxArea > area ? maxArea : area;
        }
        return maxArea;
    }
    private int countArea(int height1, int height2, int width){
        int result = 0;
        int height = height1 > height2 ? height2 : height1;
        result = height * width;
        return result;
    }
}

but only faster 15.40% of Java online submissions for Container With Most Water.

讨论区看见O(n)的算法：

（1）left = 0, right = n-1,计算left~right之间的面积

（2）若left的高度小于right的高度，则查找2~n-1之间大于left的位置，更新left，计算面积；否则，查找中间大于right高度的位置，作为新right，计算面积

（3）直到right< left

思考：

　　设以left=1为基点不变，找到一个right值，使left~right之间的矩形面积最大，则存在以下三种情况：

①a_left > a_right

　　此时高度height=a_right，width=（n-1），所求面积可能小于等于以a1为左边的最大面积。

②a_right为右边起第一个大于等于a_left的边，设right=n-1

　　此时height=a_left，width= (n-1)-1，面积有可能等于为以a1为左边的最大面积。

③a_right不为右边起第一个大于等于a_left的边，设right=n-2

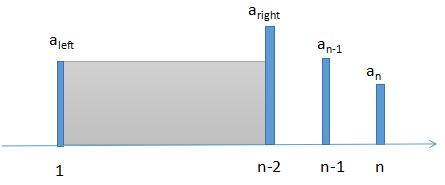
　　此时虽然height=a_left，但是width=(n-2)-1小于②中的width，所以③中求得的面积小于②中的面积，即③中的情况是不考虑的。

　　所以可以两头推进。参考如下代码：

class Solution {
    public int maxArea(int[] height) {
        int max = 0, left = 0, right = height.length-1;
        while(left < right){
            int area = Math.min(height[left],height[right]) * (right - left);
            max = max > area ? max : area;
            if(height[left] < height[right]){
                int base = height[left];
                while((height[left] <= base) && (left < right)){
                    left++;
                } // end while
            }
            else{
                int base = height[right];
                while((height[right] <= base) && (left < right)){
                    right--;
                } // end right
            } // end if-else
        } // end while
        return max;
    } // end maxArea
}

Runtime: 7 ms, faster than 55.28% of Java online submissions for Container With Most Water.

算法很重要　

一个3ms的代码：

class Solution {
　　public int maxArea(int[] height) {
　　　　int maxarea = 0;
　　　　int temparea = 0;
　　　　int i = 0;
　　　　int j = height.length -1;
　　　　while(i < j) {
　　　　　　if(height[i] <= height[j]) {
　　　　　　　　temparea = height[i] * (j-i);
　　　　　　　　i++;
　　　　　　}
　　　　　　else {
　　　　　　　　 temparea = height[j] * (j-i);
　　　　　　　　 j--;
　　　　　　}
　　　　　　if(temparea > maxarea) {
　　　　　　　　 maxarea = temparea;
　　　　　　}
　　　　}
　　　　return maxarea;
　 }
}