决策树（decision tree）

决策树是一种常见的机器学习模型。形象地说，决策树对应着我们直观上做决策的过程：经由一系列判断，得到最终决策。由此，我们引出决策树模型。

一、决策树的基本流程

---

决策树的跟节点包含全部样例，叶节点则对应决策结果。其它每个节点则对应一个属性测试，每个节点包含的样本集合根据属性测试结果被划分到不同子节点中。决策树学习的目的是，产生一棵泛化能力强，i.e.处理未见示例能力强的决策树。

决策树的基本流程遵循分治策略。基本算法的伪码书中已经给出：

从中看出，决策树是一个递归过程，有三种情形会导致递归返回：

1. 当前节点包含的样本全属于同一类别，无需划分；
2. 当前属性集为空，或所有样本在所有属性上取值相同，无法划分。此情形下，将当前节点标记为叶节点，并将其类别设为包含样本最多的类别。
3. 当前节点包含的样本集合为空，不能划分。此情形下，标记当前节点为叶节点，并将其类别设为父节点所含样例最多的类别。

情形2和3的处理之不同在于：2利用当前节点的后验分布，而3则是把父节点的样本分布作为当前节点的先验分布。

二、划分选择

---

从书中给出的伪码可以看出，决策树的关键在第8行，即如何选择最优的划分属性。一般而言，随着划分的不断进行，我们希望决策树的分支节点的“纯度”（purity）越来越高，即包含的样例尽可能多得属于同一类别。为度量纯度，我们首先需要引入信息熵和信息增益的概念。

2.1 信息增益

“信息熵”（information entropy）是度量信息纯度的一个常用指标，计算的是为了解这某条信息所付出的平均信息量。其定义如下：

假定当前样本集合D中第k类样本所占的比例为p_k(k = 1,2,...,|Y|)，则D的信息熵定义为

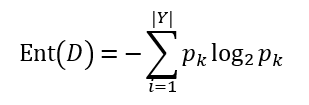
对于底数之所以取2，一般的理解是，因为信息按照计算机表示采用的是二进制形式。由定义可推知，Ent(D)的值越小，则D的纯度越高。

在此基础上，给出“信息增益”（information gain）的定义：

假定离散属性a有V种不同的取值{a¹, a², ..., a^V}，使用a对D进行划分，则会产生V个分支节点，其中第v个分支节点包含D中属性值为a^v的样本，记为D^v，则用属性a对样本集D进行划分所获得的信息增益定义为

一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的纯度提升越大。于是，我们便可以按信息增益来选择决策树的划分属性。相关的算法有著名的ID3算法[Quinlan, 1986]。

然而事实上，信息增益对可取值数目较多的属性有所偏好。这种偏好可能会降低模型的泛化能力。为减少这种偏好带来的不利影响，著名的C4.5决策树算法[Quinlan, 1993]不直接使用信息增益，而使用“增益率”（gain ratio）来划分最优属性。下面引入增益率的概念。

2.2 增益率

采用与信息增益相同的表达式，增益率定义为

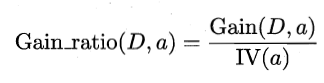
其中，

称为属性a的“固有值”（intrinsic value）[Quinlan, 1993]。属性a的可能取值数目越多（即V越大），则IV(a)的值通常会越大。

不过，增益率准则对于可取值数目少的属性又有所偏好，因此，C4.5算法并不是直接选择增益率最大的候选划分属性，而使用一个启发式算法：先从候选划分属性中找出信息增益高出平均水平的属性，再从中选择增益率最高的。

2.3 基尼系数

CART（Classification and Regression Tree）决策树[Breiman et al., 1984]则使用“基尼系数”（Gini index）来选择划分属性。数据集D的纯度可用基尼系数度量如下：

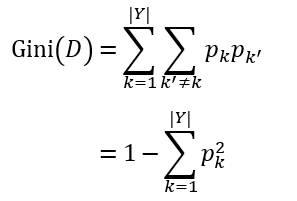
直观地讲，Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，Gini(D)越小，D的纯度越高。

在此基础上，给出属性a的基尼指数

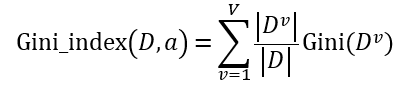
于是，我们可以选择基尼指数最小的属性作为最优划分属性。

三、决策树的剪枝处理

---

决策树的分支过多时，可能导致“过拟合”。剪枝（pruning）是决策树学习算法中解决“过拟合”的主要手段。

决策树的剪枝的基本策略主要有：

• 预剪枝（prepruning）：在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点不能提升决策树的泛化性能，则停止划分并将当前节点标记为叶节点；
• 后剪枝（postpruning）：先从训练集生成一棵决策树，然后自底向上考察非叶节点，若将该节点替换为叶节点能提升决策树的泛化性能，则将该节点替换为叶子节点。

为考察泛化能力，可以预留一部分“验证集”以进行模型评估。

值得注意的是，预剪枝虽然显著减少了训练时间和测试时间的开销，但却带来了欠拟合的风险。因为有些分支可能在当前划分无法提升泛化性能，却在后续划分中可以做到。而后剪枝决策树在一般情形下欠拟合风险更小，且泛化性能往往优于预剪枝决策树，不过代价是要付出大得多的训练时间开销。

顺便一提，经过剪枝后，仅有一层划分的决策树，也被称为“决策树桩”（decision stump）。

四、连续与缺失值

---

4.1 连续值处理

前面讨论的是基于离散属性生成的决策树。然而在现实任务中，时常会遇到连续属性，此时便不能直接根据连续属性的值来划分节点。需要对连续属性离散化。

最简单的策略是二分法（bi-partition）。给定样本集D和连续属性a，假定a在D上出现n个不同的取值，从小到大排序记为{a¹, a², ..., aⁿ}。于是，对于连续属性a，可以考虑n-1个元素的候选划分点集合T_a = {(a_i+a_i+1)/2 | 1 ≤ i ≤ n-1}。于是，在此基础上，可以对信息增益加以改造

4.2 缺失值处理

现实任务中，也会遇到大量样本出现缺失值的情况。如果简单放弃不完整样本，显然是对数据的极大浪费。为充分利用数据，需要解决两个问题：

1. 如何在属性值缺失的情况下进行划分属性选择？
2. 给定划分属性，若样本在该属性上缺失，如何对样本进行划分？

给定训练集D和属性a，令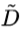表示D中在属性a上没有缺失的样本子集。对于问题1，显然仅可以根据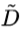来判断属性a的优劣。假定属性a有V个可取的值{a¹, a², ..., a^V}，令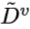表示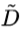中在属性a上取值为a^v的样本子集，表示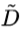中属于第k类（k=1,2,...,|Y|）的样本子集。则显然有

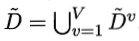
假定为每个样本x赋以权重ω_x，并定义

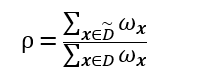
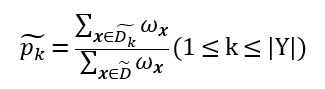
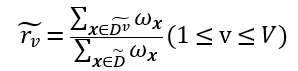
显然，，。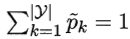

基于上述定义，可以将信息增益公式推广为

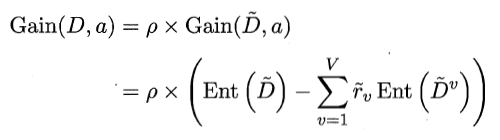
对于问题2，若样本x在属性a上的取值已知，则划入对应子节点，并保持样本权值即可；若取值未知，则同时划入所有子节点，且样本权值在属性值a^v对应的子节点中调整为。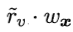

五、多变量决策树

---

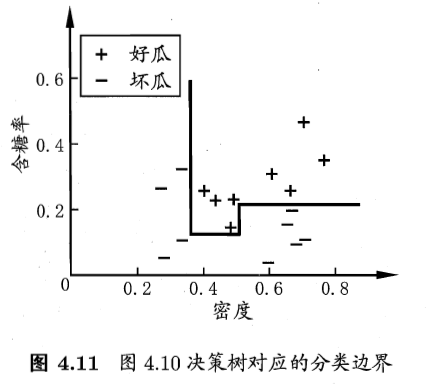
将每个属性视为坐标空间的一个坐标轴，则由d个属性描述的样本，对应于d维空间中的一个数据点。对样本分类，意味着在此坐标空间中寻找不容类样本间的分类边界。而决策树所形成的分类边界 有一个明显的特点：轴平行（axis-parallel），即其分类边界由若干个与轴平行的分段组成。这一特点的好处在于有较好的可解释性，但为了近似比较复杂的分类边界，会导致决策树过于复杂。为解决此问题，引入多变量决策树。

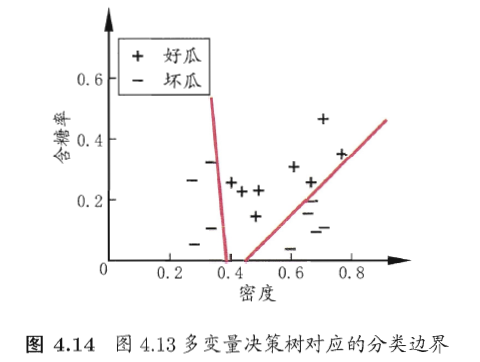
多变量决策树（multivariate decision tree）就能实现用斜线划分、甚至更复杂的划分。在此类决策树中，非叶节点不再仅是某个属性，而是对属性的线性组合进行测试，i.e.每个非叶节点都是一个形如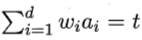的线性分类器。下面两张图给出了决策树和多变量决策树分类结果的对比。