主成分分析 —PCA

一.定义

　　主成分分析（principal components analysis)是一种无监督的降维算法，一般在应用其他算法前使用，广泛应用于数据预处理中。其在保证损失少量信息的前提下，把多个指标转化为几个综合指标的多元统计方法。这样可达到简化数据结构，提高分信息效率的目的。

　　通常，把转化生成的综合指标称为主成分，其中每个成分都是原始变量的线性组合，且每个主成分之间互不相关，使得主成分比原始变量具有某些更优越的性能。

　　一般，经主成分分析分析得到的主成分与原始变量之间的关系有：

• （1）每个主成分都是各原始变量的线性组合
• （2）主成分的数目大大骚鱼原始变量的数目
• （3）主成分保留了原始变量的绝大多数信息
• （4）各主成分之间互不相关

二.过程

　　其过程是对坐标系旋转的过程，各主成分表达式就是新坐标系与原坐标系的转换关系，在新坐标系中，各坐标轴的方向就是原始数据变差最大的方向。（参见《多元统计分析》P114-117,新坐标轴Y1和Y2，用X1和X2的线性组合表示，几何上是将坐标轴按逆时针方向旋转一定的角度而得出）

　　详细版：数据从原来的坐标系转换到新的坐标系。转换坐标系时，以方差最大的方向作为新坐标轴方向（数据的最大方差给出了数据的最重要的信息）。第一个新坐标轴选择的是原始数据中方差最大的方法，第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复以上过程，重复次数为原始数据的特征维数。

　　在重复中，我们不断地得到新的坐标系。Generally,方差集中于前面几个综合变量中，且综合变量在总方差中所占的比重依次递减，而后面新的坐标轴所包含的方差越来越小，甚至接近0。实际应用中，一般只要挑选前几个方差较大的主成分即可。

　　那么，我们如何得到这些包含最大差异性的主成分方向呢？事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值及特征向量，选择特征值最大（也即包含方差最大）的N个特征所对应的特征向量组成的矩阵，我们就可以将数据矩阵转换到新的空间当中，实现数据特征的降维（N维）。

　　由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵，所以PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。（特征值分解最大的问题是只能针对方阵，即n*n的矩阵。而在实际的应用中，我们分解的大部分都不是方阵，所以产生了SVD。）

三.Python实现

1.sklearn.decomposition.PCA

　　sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None)

它利用SVD分解协方差矩阵实现PCA算法，实现降维效果。

　　注意：此类不适用于稀疏数据。

　　参数：

　　（1）n_components : 整型, 浮点型, None or 字符串类型。设置最后保留下来的主成分个数。

如果不设置该参数，则保留所有主成分。

赋值为string，如n_components='mle'，将自动选取特征个数n，使得满足所要求的方差百分比。

　　（2）copy : 布尔值 (默认值 True)。表示在运算时，是否将原始数据复制一遍。

True:运算后，原始数据不会变化，因为运算是在原始数据的副本上进行的。

False：算法运算将在原始数据上运行，原始数据最终发生变化。

　　（3）whiten : 布尔值(默认 False)

True:对降维后的主成分进行归一化，使所有主成分的方差为1。

一般不白化，使用默认的False即可。

　　（4）svd_solver :指定奇异值分解SVD的方法。字符串，{auto、 full、arpack、 randomized}

auto :默认值。该类会自行选择以下三种中最佳的一种来实现算法。一般使用默认值即可。

full :传统意义的SVD，使用了scipy库的对应实现法。

arpack :用于数据量较大、维度较多，最后主成分较少的情况。

randomized :一般用于数据量大，数据维度多，且主成分较少的情况。

　　（5）random_state :设置复现的参数。

2.属性:

（1）components_ ：返回降维后各主成分方向，并按照各主成分的方差值大小排序。

（2）explained_variance_ ：降维后各主成分的方差值

（3）explained_variance_ratio_ ：返回各个成分的方差百分比（贡献率）

（4）n_components_ ：返回所保留的成分个数n。

3.例1：iris数据集

import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.decomposition import PCA     #主成分分析用
from mpl_toolkits.mplot3d import Axes3D  #画三维图

# 导入鸢尾花数据
iris = datasets.load_iris()
x, y = iris.data, iris.target

print("x:", x.shape)
print("y:", y.shape)
print("原始变量名：", iris.feature_names)
print("标签分类：",iris.target_names)

x: (150, 4)
y: (150,)
原始变量名： ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
标签分类： ['setosa' 'versicolor' 'virginica']

有150个样本，每个样本有四个特征：萼片长度、萼片宽度、花瓣长度、花瓣宽度，根据上诉四个特征，将150个样本分成三类。

pca0 = PCA(n_components=4)
pca0.fit(x).transform(x)
print("四个主成分方向：\n", pca.components_)

四个主成分方向：
 [[ 0.36158968 -0.08226889  0.85657211  0.35884393]
 [ 0.65653988  0.72971237 -0.1757674  -0.07470647]
 [-0.58099728  0.59641809  0.07252408  0.54906091]
 [ 0.31725455 -0.32409435 -0.47971899  0.75112056]]

假设原始变量为x1、x2、x3、x4, Y1为新的第一个主成分，则可认为Y1 = 0.36158968x1 - 0.08226889x2 + 0.85657211x3 + 0.35884393x4,以此类推，可写出Y2、Y3、Y4。

print("各主成分的方差值：\n",pca.explained_variance_)
print("各主成分的方差值占比：\n",pca.explained_variance_ratio_)

各主成分的方差值：
 [ 4.22484077  0.24224357  0.07852391  0.02368303]
各主成分的方差值占比：
 [ 0.92461621  0.05301557  0.01718514  0.00518309]

第一个主成分占方差百分比的92.5%，第二个主成分占百分比的5.3%，第三个主成分占百分比的0.2%，前面三个主成分已包含原始变量中99%的信息，现在剔除最后一个主成分，仅保留前三个主成分。

pca1 = PCA(n_components=3)
pca1.fit(x)
x1_new = pca1.transform(x)
print("前三个主成分方向:\n",pca1.components_)
print("各主成分的方差值：\n",pca1.explained_variance_)
print("各主成分的方差值占比：\n",pca1.explained_variance_ratio_)

前三个主成分方向:
 [[ 0.36158968 -0.08226889  0.85657211  0.35884393]
 [ 0.65653988  0.72971237 -0.1757674  -0.07470647]
 [-0.58099728  0.59641809  0.07252408  0.54906091]]
各主成分的方差值：
 [ 4.22484077  0.24224357  0.07852391]
各主成分的方差值占比：
 [ 0.92461621  0.05301557  0.01718514]

fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x1_new[:,0],x1_new[:,1],x1_new[:,2],c=y)

<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0xe352bb35c0>

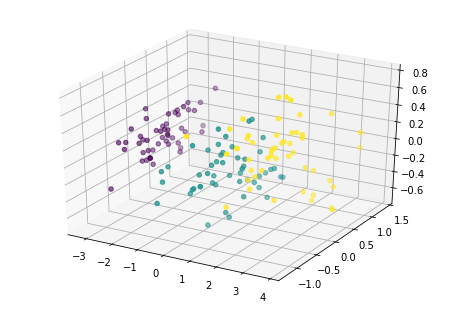
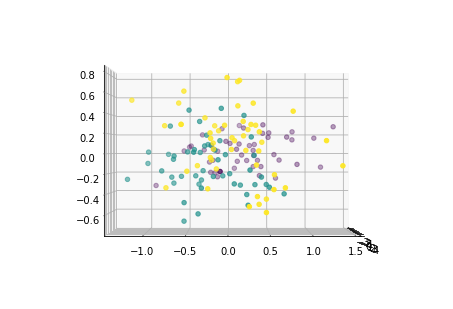
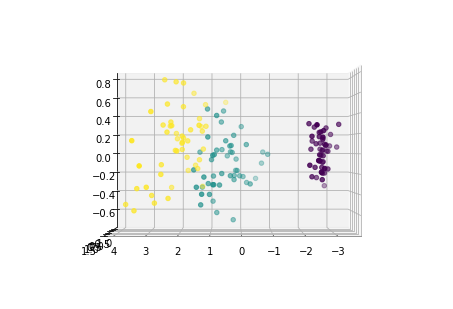
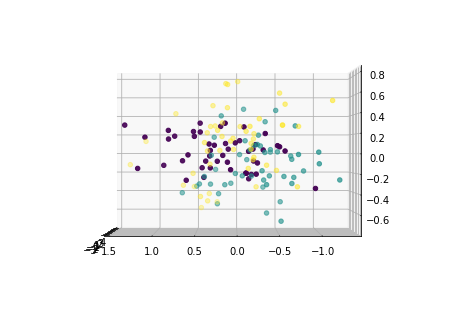
下面从多个角度来看各主成分的分布情况：

for i in [0,90,180,270]:
    fig = plt.figure()
    ax = Axes3D(fig,elev=0, azim=i)
    ax.scatter(x1_new[:,0],x1_new[:,1],x1_new[:,2],c=y)

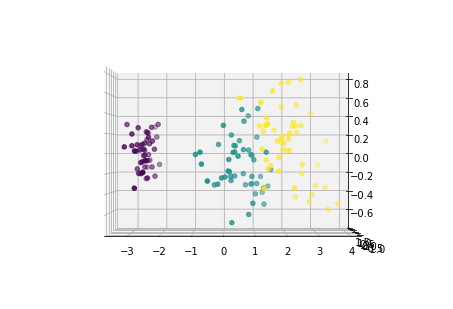
for i in [0,90,180,270]:
    fig = plt.figure()
    ax = Axes3D(fig,elev=i, azim=0)
    ax.scatter(x1_new[:,0],x1_new[:,1],x1_new[:,2],c=y)

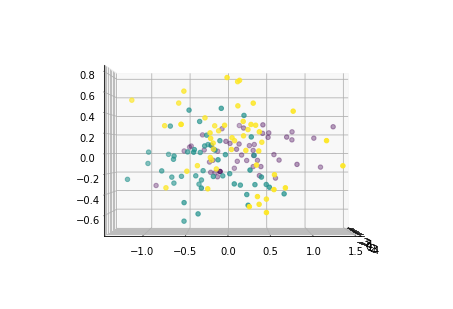
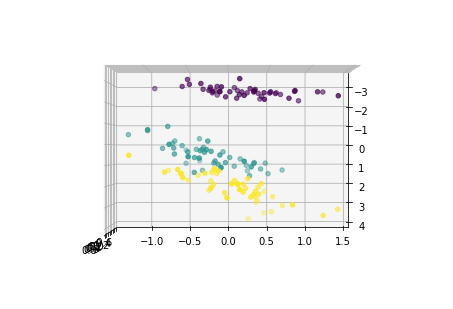
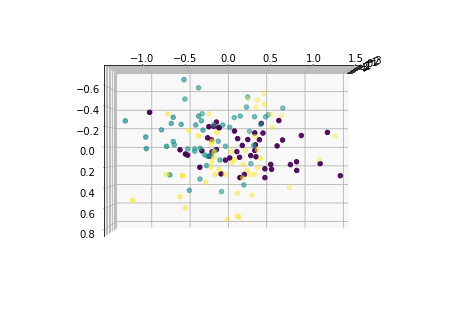
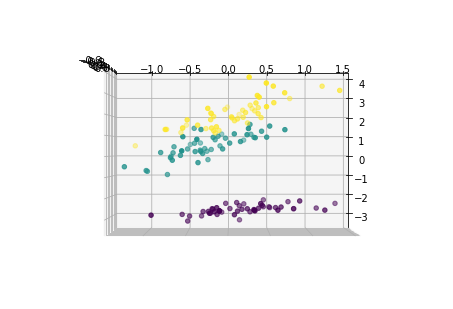
pca2 = PCA(n_components=2)
pca2.fit(x)
x2_new = pca2.transform(x)
print("2个主成分方向：\n", pca2.components_)
print("2个主成分的解释方差值：\n", pca2.explained_variance_)
print("2个主成分解释方差占比：\n", pca2.explained_variance_ratio_)
plt.scatter(x2_new[:,0],x2_new[:,1],c=y)

2个主成分方向：
 [[ 0.36158968 -0.08226889  0.85657211  0.35884393]
 [ 0.65653988  0.72971237 -0.1757674  -0.07470647]]
2个主成分的解释方差值：
 [ 4.22484077  0.24224357]
2个主成分解释方差占比：
 [ 0.92461621  0.05301557]

<matplotlib.collections.PathCollection at 0xe353a2af98>

四.PCA的缺点

1.各个主成分的含义具有模糊性，不具有原始变量的清晰含义。

2.方差小的主成分可能含有对样本差异的重要信息，那么降维后可能影响后续的数据分析。