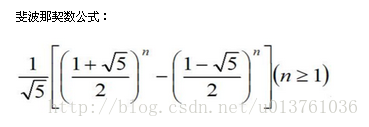hdu1568斐波那契前4位
题意:
就是求斐波那契数,但是只要求输出前四位,(n<=100000000)。
思路:
这个要用到斐波那契的公式和一些log的规律,直接打看着很乱,直接在网上偷张图片吧:
然后就是一些log的性质
log10(a^b) = b * log10(a),log10(a*b) = log10(a) + log10(b)
我们可以根据这个把大数的前几位拿出来,这样:
log10(1234567890)
= log10(1.234567890 * 10^9)
= log10(1.234567890) + 9
这样我们就得到了一个"小数部分"bit = log10(1.234567890)
然后pow(10.0 ,bit) = 1.234567890
这样我们就得到了一个大数的科学技术法的前边部分,想要四位,直接*1000取整就行了。
#include<stdio.h>
#include<math.h>
int num[25];
void ini()
{
num[0] = 0 ,num[1] = 1;
for(int i = 2 ;i <= 20 ;i ++)
num[i] = num[i-1] + num[i-2]; } int main ()
{
ini();
int n;
while(~scanf("%d" ,&n))
{
if(n <= 20)
{
printf("%d\n" ,num[n]);
continue;
}
double now = -0.5 * log10 (5.0) + n * 1.0 * log10((1+sqrt(5.0))/2.0);
double bit = now - (int)now;
double a = pow(10.0,bit);
a *= 1000;
printf("%d\n" ,int(a));
}
return 0;
}
hdu1568斐波那契前4位的更多相关文章
- hdu3117 斐波那契前后4位
题意: 求斐波那契的前后4位,n <= 10^8. 思路: 至于前四位,和hdu1568的求法一样: http://blog.csdn.net/u013761 ...
- AcWing 1303. 斐波那契前 n 项和
输出斐波那契数列前 n 项和 对m取摸的结果 #include<bits/stdc++.h> #define LL long long #define N 3 using namespac ...
- HDU 1568 快速求斐波那契前四位
思路: 把斐波那契通项公式转化成log的形式,高中数学... //By SiriusRen #include <bits/stdc++.h> using namespace std; ], ...
- HDU1568斐波那契推理
Fibonacci Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total S ...
- The sum - SGU 122(斐波那契前N项和)
直接上代码....... ======================================================================================= ...
- HDU 1568 Fibonacci【求斐波那契数的前4位/递推式】
Fibonacci Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Proble ...
- hdu1568&&hdu3117 求斐波那契数前四位和后四位
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1568 题意:如标题所示,求斐波那契数前四位,不足四位直接输出答案 斐波那契数列通式: 当n<=2 ...
- Python基础(二):斐波那契数列、模拟cp操作、生成8位随机密码
一.斐波那契数列 目标: 编写fib.py脚本,主要要求如下: 输出具有10个数字的斐波那契数列 使用for循环和range函数完成 改进程序,要求用户输入一个数字,可以生成用户需要长度的斐波那契数列 ...
- hdu 2160 母猪的故事(睡前随机水一发)(斐波那契数列)
解题思路: 一只母猪生下第二头后立马被杀掉,可以这样想即,生下第二头便被杀掉,可以看成母猪数量没变 第一天 1 第二天 2 第三天 3 :第一头生第二头后杀掉还是1头,第二头再加上第二头生下的,一共三 ...
随机推荐
- 面试常备,字符串三剑客 String、StringBuffer、StringBuilder
尽人事,听天命.博主东南大学硕士在读,热爱健身和篮球,乐于分享技术相关的所见所得,关注公众号 @ 飞天小牛肉,第一时间获取文章更新,成长的路上我们一起进步 本文已收录于 「CS-Wiki」Gitee ...
- vscode配置golang开发环境手把手描述篇
1.下载安装Golang https://golang.google.cn/dl/ 一路下一步即可 2.下载安装Vscode https://visualstudio.microsoft.com/zh ...
- kali Linux树莓派的完整配置,以及python环境的配置
kali Linux树莓派3b+的环境配置,以及python开发环境的配置 首先需要正确组装树莓派的硬件,所需:一块8G以上的内存卡,(一般情况下淘宝购买的时候都会选择一个,需要一个稳定的电源输出,防 ...
- 为 .NET 打 Call,为国产平台 Gitee 打 Call,我的 .NET/C# 开源项目清单,同步维护于 Github 和 Gitee
所有项目遵循 MIT 开源协议.可以随意使用,但是需在源代码和产品关于画面保留版权声明和我的网站链接,谢谢. Sheng.Winform.IDE Github:https://github.com/i ...
- Anchor-Free总结
目录 Anchor-Free综述 一. CornerNet 1.1 概述 1.2 模块介绍 1.2.1 Heatmap 1.2.2 Offset 1.2.3 Grouping Corners 1.2. ...
- Blind Super-Resolution Kernel Estimation using an Internal-GAN 论文解读
背景与思路来源 目前 SR 模型中合成 LR 使用的模糊核问题 目前大多数 SR 的 model 都是用的合成下采样图片来进行训练的,而这些合成的图片常常使用的是 MATLAB 里面的 imresiz ...
- io流(对象流总结)
对象流 对象流就是对引用数据类型进行操作 序列化:将对象的状态信息转换为可以存储或传输的形式的过程,因此类需要序列化后才可以存储到文件中 对象输出流: 很简单,就三句话,将把一个对象导入指定文件中,要 ...
- Linux—用户新建目录和文件的默认权限设置:umask详解
关注微信公众号:CodingTechWork,一起学习进步. 引言 我们有没有思考过一个问题,在登录Linux系统后,我们创建的目录或者文件的权限,为什么每次创建都是统一的?我们做以下实验:新建一 ...
- Windows + Jenkins + .NetFramework + SVN 持续部署
Windows + Jenkins + .NetFramework + SVN 持续部署 环境准备 服务端环境 安装 Windows 服务器 1.阿里云购买临时服务器 阿里云:https://www. ...
- 14、运行Django时浏览器中遇到Refused to display 'url' in a frame because it set 'X-Frame-Options' to 'deny'
问题:Refused to display 'url' in a frame because it set 'X-Frame-Options' to 'deny' 解决办法: 只需要在 Djagno ...