【SCOI2007】组队(单调性)

题目链接

大意

给定\(N\)个人与三个常量\(A,B,C\)，每个人有两个属性：\(Hi\),\(Vi\).

现要让你选些人出来，定义\(Hmin\)为选出来的这些人中最小的\(Hi\)值，\(Vmin\)同理.

对于选出来的这些人，每个人都要满足$$A\cdot Hi+B\cdot Vi\le A\cdot Hmin+B\cdot Vmin+C$$

求最多能选出多少人。

(满足\(N\le 5000\))

思路

对于给出的条件，简列一下就是：

\[\begin{cases}
①~A\cdot Hi+B\cdot Vi\le A\cdot Hmin+B\cdot Vmin+C\\
②~Hi\ge Hmin\\
③~Vi\ge Vmin\\
\end{cases}\]

首先，易得一个\(O(N^3)\)的算法：暴力枚举\(Hmin,Vmin\)，再对每个人，看是否满足以上条件。

考虑优化：

首先观察数据范围，发现支持\(O(N^2)\)的做法。

那么先随便枚举一个\(Hmin\)出来（以下推导均已满足\(Hmin\le Hi\)）。

考虑在枚举\(Vmin\)时，如何统计：

我们设\(Si=A\cdot Hi+B\cdot Vi\)，那么对于一个可以被选的点应满足

\[\begin{cases}
①Vi\ge Vmin\\
②Si\le C+A\cdot Hmin+B\cdot Vmin\\
\end{cases}\]

发现在\(Vmin\)值变大的时候，式子的右边都是单调递增的。

所以我们按照\(Vi\)排序，再枚举一个\(Vmin\)出来。

---

然后对于一个人，我们可以这样想，把它想成二维平面上的一个点\((Vi,Si)\)

那么就会有两个限制

\[\begin{cases}
①Vi\ge Vmin\\
②Si\le C+A\cdot Hmin+B\cdot Vmin\\
\end{cases}\]

设有两条直线：$$L1:X=Vmin$$$$L2:Y=C+A\cdot Hmin+B\cdot Vmin$$

那么在\(Vmin\)值变大的时候，\(L1\)右移，\(L2\)上移，如图：



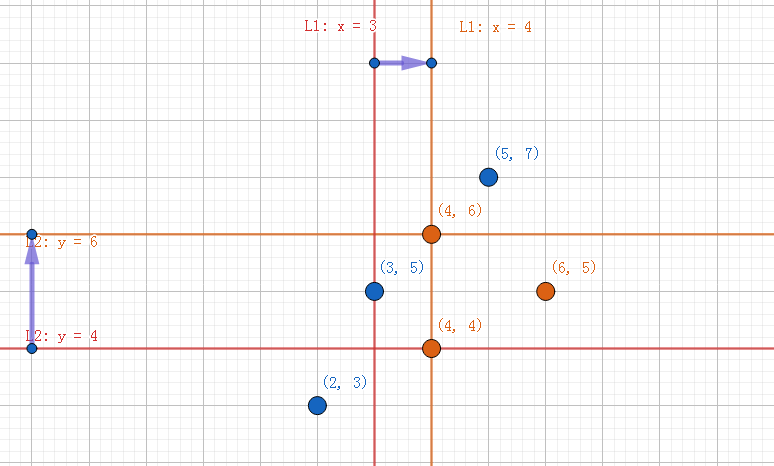
那么对应的，\(L1\)经过的点的\(Vi\)肯定都小于当前的\(Vmin\)，故\(L1\)经过的都不合法。

而当前合法的点肯定会被\(L2\)经过。(包含当前\(L2\)上点)

所以，我们就可以在\(Vmin\)增大时，用什么Vis数组之类的动态维护答案，不断取Max值就行了。

代码

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
#define LL long long
const int MAXN=5005;
const int MAXV=10000;
int N,Ans,Vis[MAXN];
long long A,B,C;
struct Node{int H,V,id;LL S;};
Node s1[MAXN],s2[MAXN],s3[MAXN];
bool cmpH(Node X,Node Y){return X.H<Y.H;}
bool cmpV(Node X,Node Y){return X.V<Y.V;}
bool cmpS(Node X,Node Y){return X.S<Y.S;}
int main(){
	//freopen("team.in","r",stdin);
	//freopen("team.out","w",stdout);
	scanf("%d%lld%lld%lld",&N,&A,&B,&C);
	for(int i=1;i<=N;i++){
		scanf("%d%d",&s1[i].H,&s1[i].V);
		s1[i].S=s1[i].H*A+s1[i].V*B;s1[i].id=i;
		s2[i]=s3[i]=s1[i];
	}
	sort(s2+1,s2+N+1,cmpV);
	sort(s3+1,s3+N+1,cmpS);
	for(int i=1;i<=N;i++){
		int Hmin=s1[i].H;
		int p1=1,p2=1,cnt=0;
		for(int j=1;j<=N;j++)Vis[j]=0;
		for(int j=1;j<=N;j++){
			int Vmin=s2[j].V;
			for(;p1<=N&&s3[p1].S<=C+Hmin*A+Vmin*B;p1++)
				if(s3[p1].H>=Hmin)cnt+=(Vis[s3[p1].id]==0),Vis[s3[p1].id]=1;
			for(;p2<=N&&s2[p2].V<Vmin;p2++)
				if(s2[p2].H>=Hmin)cnt-=Vis[s2[p2].id],Vis[s2[p2].id]=1;
			Ans=max(Ans,cnt);
		}
	}
	printf("%d\n",Ans);
}
/*
H*A+V*B<=C+Hmin*A+Vmin*B
H>=Hmin  V>=Vmin
*/