DP+单调队列详解+题目

介绍：

单调队列优化的原理

先回顾单调队列的概念，它有以下特征：

（1）单调队列的实现。用双端队列实现，队头和队尾都能插入和弹出。手写双端队列很简单。

（2）单调队列的单调性。队列内的元素具有单调性，从小到大，或者从大到小。

（3）单调队列的维护。每个新元素都能进入队列，它从队尾进入队列时，为维护队列的单调性，应该与队尾比较，把破坏单调性的队尾弹出。例如一个从小到大的单调队列，如果要进队的新元素a比原队尾v小，那么把v弹走，然后a继续与新的队尾比较，直到a比队尾大为止，最后a进队尾。

单调队列在DP优化中的基本应用，是对这样一类DP方程进行优化：

$ d p [ i ] $= m i n { $ d p [ j ] + a [ i ] + b [ j ] $ } $L ( i ) ≤ j ≤ R ( i )$ --方程(1)

公式中的$min$也可以是$max$。方程的特点是其中关于$i$的项$a[i]$和关于$j$的项$b[j]$是独立的。$j$被限制在窗口$[L(i),R(i)]$内，常见的例如给定一个窗口值$k$，$i − k ≤ j ≤ i $。这个DP方程的编程实现，如果简单地对i做外层循环，对j做内层循环，复杂度 $O( n^2 )$。如果用单调队列优化，复杂度可提高到$O(n)$。

为什么单调队列能优化这个DP方程？

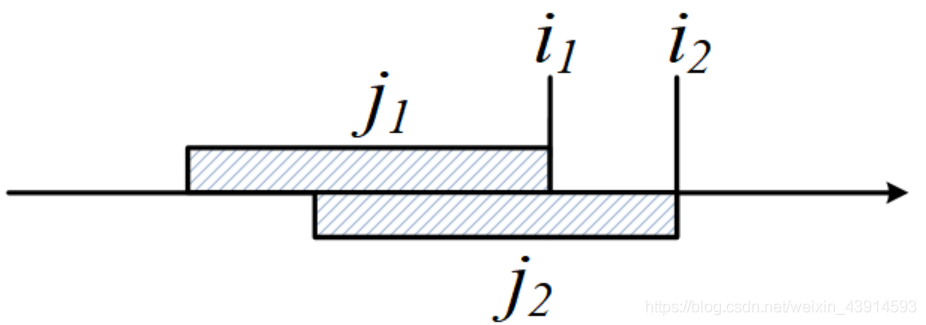
概况地说，单调队列优化算法能把内外 $ i、j $ 两层循环，精简到一层循环。其本质原因是“外层 $ i $ 变化时，不同的 $ i $ 所对应的内层 $ j $ 的窗口有重叠”。如下图所示，$ i = i_1 $时，对应的 $ j_1 $ 的移动窗口（窗口内处理DP决策）范围是上面的阴影部分,$ i = i_2 $ 时，对应的 $j_2$ 处理的移动窗口范围是下面的阴影；两部分有重叠。当 $ i $ 从 $ i_1 $ 增加到 $ i_2 $ 时，这些重叠的部分被重复计算，如果减少这些重复，就得到了优化。

主要方法：先写出没有单调队列的普通DP，在加上单调队列，即可

题目

代码比较明了就没加注释

）逃

P1886 滑动窗口 /【模板】单调队列

#include <bits/stdc++.h>
using namespace std;
const int N = 2000005;
int n,l,r;
int a[N];
int dp[N],dq[N];
int head=1,tail=0;
int maxx=-0x3f3f3f,ans=-0x3f3f3f;
int main(){
	memset(dp,-0x3f3f3f,sizeof(dp));
	scanf("%d%d%d",&n,&l,&r);
	for (int i=0;i<=n;i++)
		scanf("%d",&a[i]);
	dp[0]=0;
	for (int i=l;i<=n+r;i++){
		while (head<=tail&&dq[head]<i-r)
			head++;
		while (head<=tail&&dp[dq[tail]]<=dp[i-l])
			tail--;
		dq[++tail]=i-l;
		int temp=dp[dq[head]];
		dp[i]=temp+a[i];
	}
	for (int i=n;i<=n+r;i++)
		ans=max(ans,dp[i]);
	printf("%d",ans);
	return 0;
}

P2627 [USACO11OPEN]Mowing the Lawn G

【Description】

　　在一年前赢得了小镇的最佳草坪比赛后，FJ变得很懒，再也没有修剪过草坪。现在，新一轮的最佳草坪比赛又开始了，FJ希望能够再次夺冠。

　　然而，FJ的草坪非常脏乱，因此，FJ只能够让他的奶牛来完成这项工作。FJ有N(1 <= N <= 100,000)只排成一排的奶牛，编号为1…N。每只奶牛的效率是不同的，奶牛i的效率为E_i(0 <= E_i <= 1,000,000,000)。

靠近的奶牛们很熟悉，因此，如果FJ安排超过K只连续的奶牛，那么，这些奶牛就会罢工去开派对:)。因此，现在FJ需要你的帮助，计算FJ可以得到的最大效率，并且该方案中没有连续的超过K只奶牛。

【Input】

　　* 第一行：空格隔开的两个整数N和K

　　* 第二到N+1行：第i+1行有一个整数E_i

【Output】

　　* 第一行：一个值，表示FJ可以得到的最大的效率值

【Sample Input】

【Sample Output】

【Hint】

　　FJ有5只奶牛，他们的效率为1，2，3，4，5。他们希望选取效率总和最大的奶牛，但是他不能选取超过2只连续的奶牛

　　FJ可以选择出了第三只以外的其他奶牛，总的效率为1+2+4+5=12。

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
ll f[maxn],g[maxn],s[maxn];
int n,k,q[maxn],a[maxn];
int main()
{
    scanf("%d%d",&n,&k);
    for (int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		s[i]=s[i-1]+a[i];
	}
    int l=1,r=1;
    for (int i=1;i<=n;i++)
    {
        while(l<r&&i-q[l]>k)l++;
        f[i]=g[q[l]]-s[q[l]]+s[i];
        g[i]=max(f[i-1],g[i-1]);
        while(l<=r&&g[q[r]]-s[q[r]]<=g[i]-s[i])r--;
        q[++r]=i;
    }
    printf("%lld\n",max(f[n],g[n]));
    return 0;
}

P1725 琪露诺

#include <bits/stdc++.h>
using namespace std;
const int N = 2000005;
int n,l,r;
int a[N];
int dp[N],dq[N];
int head=1,tail=0;
int maxx=-0x3f3f3f,ans=-0x3f3f3f;
int main(){
	memset(dp,-0x3f3f3f,sizeof(dp));
	scanf("%d%d%d",&n,&l,&r);
	for (int i=0;i<=n;i++)
		scanf("%d",&a[i]);
	dp[0]=0;
	for (int i=l;i<=n+r;i++){
		while (head<=tail&&dq[head]<i-r)
			head++;
		while (head<=tail&&dp[dq[tail]]<=dp[i-l])
			tail--;
		dq[++tail]=i-l;
		int temp=dp[dq[head]];
		dp[i]=temp+a[i];
	}
	for (int i=n;i<=n+r;i++)
		ans=max(ans,dp[i]);
	printf("%d",ans);
	return 0;
}