【LeetCode】119. 杨辉三角 II Pascal‘s Triangle II（Python & Java）

作者： 负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/

---

目录

• 题目描述
• 题目大意
• 解题思路
• • 方法一： 空间复杂度

    O

    (

    k

    ∗

    (

    k

    +

    1

    )

    /

    2

    )

    O(k * (k + 1) / 2)

    O(k∗(k+1)/2)

  • 方法二：空间复杂度

    O

    (

    k

    )

    O(k)

    O(k)

• 刷题心得
• 日期

[LeetCode]

题目地址：[https://leetcode.com/problems/pascals-triangle-ii/][1]

Total Accepted: 74643 Total Submissions: 230671 Difficulty: Easy

题目描述

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.

Note that the row index starts from 0.

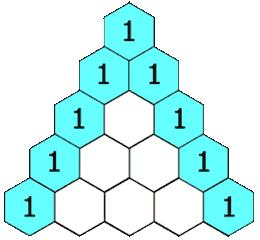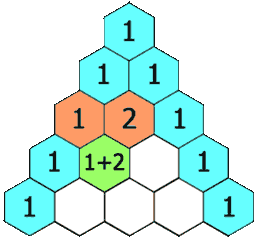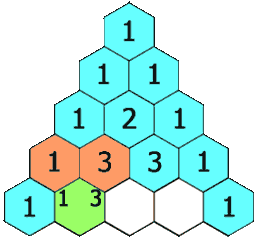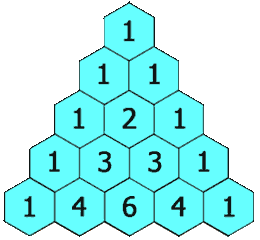
In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O(k) extra space?

题目大意

计算杨辉三角的第k行是多少。

解题思路

本题可以有两种空间复杂度的解法：

O

(

k

∗

(

k

+

1

)

/

2

)

O(k * (k + 1) / 2)

O(k∗(k+1)/2) 和

O

(

k

)

O(k)

O(k)。下面分别介绍。

方法一： 空间复杂度

O

(

k

∗

(

k

+

1

)

/

2

)

O(k * (k + 1) / 2)

O(k∗(k+1)/2)

该方法是常见的方法，即按照新建一个二维数组 res[i][j] ，数组的每一行 res[i] 代表了杨辉三角的第

i

i

i 行的所有元素， res[i][j] 表示杨辉三角的第

i

i

i 行第

j

j

j 列的元素。。

由下面的图我们可以看出：

r

e

s

[

i

]

[

j

]

=

r

e

s

[

i

−

1

]

[

j

−

1

]

+

r

e

s

[

i

−

1

]

[

j

]

res[i][j] = res[i - 1][j - 1] + res[i - 1][j]

res[i][j]=res[i−1][j−1]+res[i−1][j]。

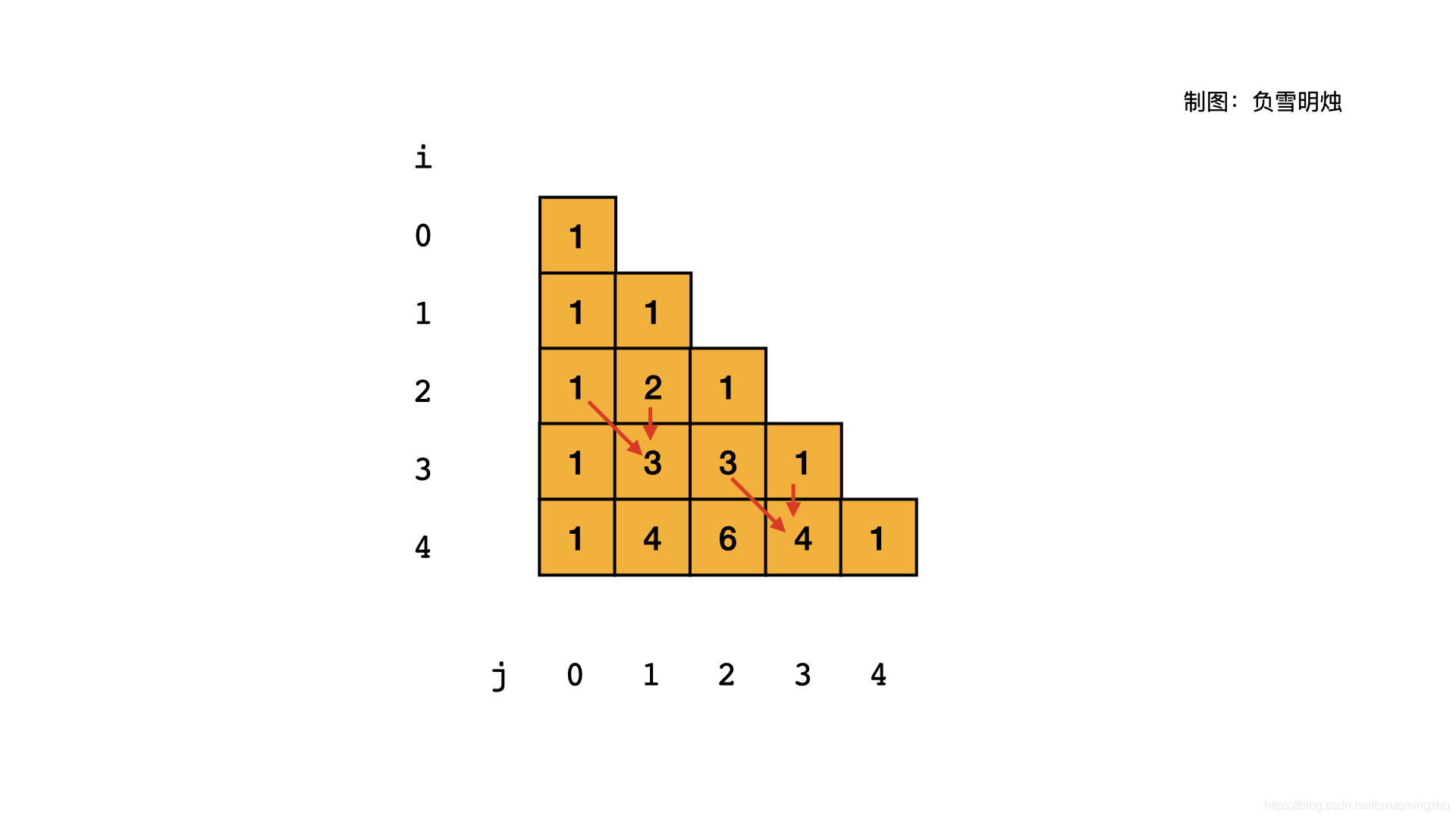
该方法对应的 Python2 代码是：

class Solution(object):
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        res = [[1 for j in range(i + 1)] for i in range(rowIndex + 1)]
        for i in range(2, rowIndex + 1):
            for j in range(1, i):
                res[i][j] = res[i - 1][j - 1] + res[i - 1][j]
        return res[-1]

方法二：空间复杂度

O

(

k

)

O(k)

O(k)

题目中给了一个进阶问题，能不能用

O

(

k

)

O(k)

O(k) 的时间复杂度呢？

其实是可以的，我们只用一个长度为

k

k

k 的一维数组。类似于动态规划中降维的思路。

使用一维数组，然后从右向左遍历每个位置，每个位置的元素

r

e

s

[

j

]

res[j]

res[j] += 其左边的元素

r

e

s

[

j

−

1

]

res[j - 1]

res[j−1]。

为啥不从左向右遍历呢？因为如果从左向右遍历，那么左边的元素已经更新为第 i 行的元素了，而右边的元素需要的是第

i

−

1

i - 1

i−1 行的元素。故从左向右遍历会破坏元素的状态。

该方法对应的 Python2 代码是：

class Solution(object):
    def getRow(self, rowIndex):
        """
        :type rowIndex: int
        :rtype: List[int]
        """
        res = [1] * (rowIndex + 1)
        for i in range(2, rowIndex + 1):
            for j in range(i - 1, 0, -1):
                res[j] += res[j - 1]
        return res

刷题心得

1. 本题的空间优化方式，类似于滚动数组，看来刷题的方法是通用的。
2. 本题也可以用公式求解。

日期

2016 年 05月 8日
2018 年 11 月 21 日 —— 又是一个美好的开始
2021 年 2 月 12 日 —— 今天是大年初一，祝大家牛年大吉！

[1]: https://leetcode.com/problems/pascals-triangle-ii1]: https://leetcode.com/problems/pascals-triangle/