[NOIP2013 提高组] 华容道 P1979 洛谷

[NOIP2013 提高组] 华容道 P1979 洛谷

强烈推荐，更好的阅读体验

经典题目：spfa+bfs+转化

题目大意:

给出一个01网格图，和点坐标x,y空格坐标a,b，目标位置tx,ty要求移动空格最少步数使点到tx,ty

本题关键:

我们可以发现本题可以用BFS获得很高的暴力分，但是也可以使用DP:

$f[i][j][x][y]表示空格在i,j目标点在x,y的最少操作次数$

但是本题的多次询问给我们一个启发-->可以预处理

所有我们可能可以预先处理一些状态的转移

可以发现很多状态是无效的，对于一个正确的移动路径:一定由两个部分组成

1.空格移动到目标格附近-->2.目标格借助空格移动到终点

对于前者很容易独立求出，对于后者，我们单独优化

目标点与空格的位置合并为一个状态,容易发现这个状态是4维的，空间卡住，时间__了

优化状态:

$f[i][j][0/1/2/3]表示目标点x=i,y=j,空格在其上下左右的相邻位置的状态$

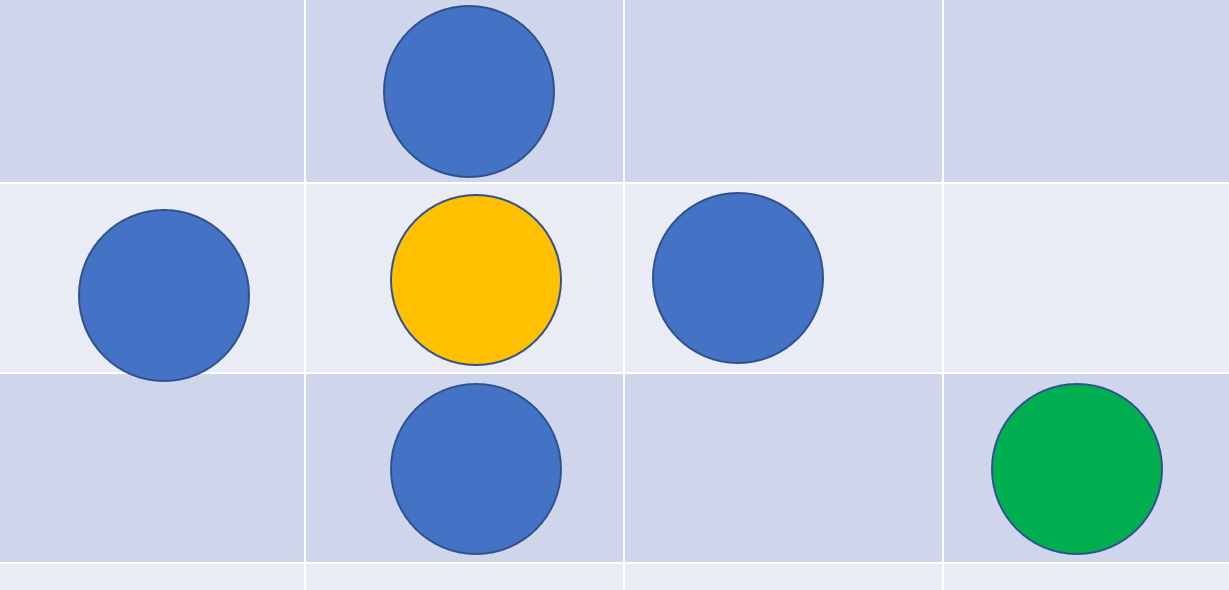
为什么可以这样定义:因为在目标格借助空格移动到终点的过程中

假设目标点是下图黄球，空格只能是蓝球不能是绿球

不需要怎么了

状态之间的联系:

相邻状态:黄球位置确定下的所有蓝球位置(有效<=4)

所有对于一个状态考虑的转移左右3+1个

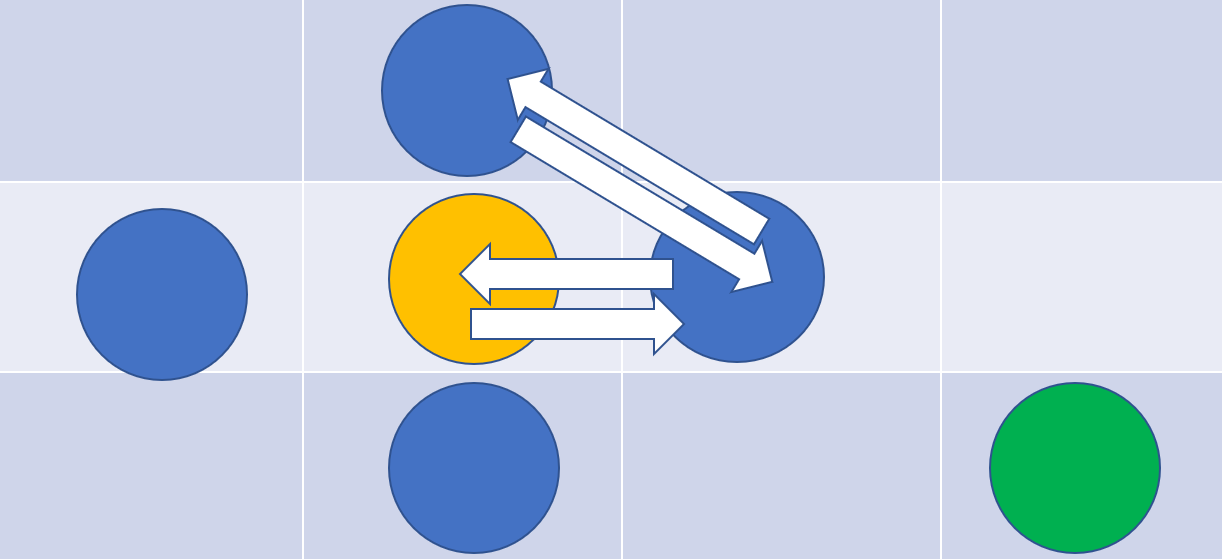
另外一个是空格目标交换位置(下图两种情况)

下面就可以上代码了

  1 //先看主函数
  2 #include<bits/stdc++.h>
  3 #define ll int
  4 #define f(i,a,b) for(ll i=a;i<=b;i++)
  5 #define fd(i,a,b) for(ll i=a;i>=b;i--)
  6 #define il inline
  7 #define gc getchar()
  8 #define r(i,a) for(ll i=fir[a];i;i=e[i].nex)
  9 const ll maxn=32,INF=1e9,half=10,maxm=1e5;
 10 ll n,m,q;
 11 using namespace std;
 12 bool Map[maxn][maxn];
 13 ll xa[10]={-1,0,1, 0,0,0,0};
 14 ll ya[10]={0, 1,0,-1,0,0,0};
 15          //下 左→  ←
 16 ll f[maxn][maxn][half],cnt;
 17 ll dis[maxn][maxn],fir[maxm];
 18 //把所有数组定义提前，以免重复或re
 19 struct edge{ll to,nex,w;}e[maxm<<1];
 20
 21 il void add(ll a,ll b,ll c){e[++cnt].to=b,e[cnt].nex=fir[a],e[cnt].w=c;fir[a]=cnt;}
 22
 23 //↑用于spfa的建边,在dfs中建边
 24 ll getnum(ll x,ll y){return ((x-1)*(m)+y)<<2;}
 25 //对于每个空格与目标个相邻的状态进行编号
 26 ll fat(ll x){return (x+2)%4;}
 27 //空格相对于目标格的位置下上右左-->上下左→
 28 queue<pair<ll,ll> >que;
 29 //记录空格在s的d方位
 30 il void bfs(ll a,ll b,ll x,ll y,ll d){//重复使用bfs
 31     //a,b是枚举格子,x,y是空格
 32     memset(dis,-1,sizeof(dis));
 33     dis[a][b]=1;//防止被加入队列
 34     dis[x][y]=0;
 35     que.push(make_pair(x,y));
 36     while(!que.empty()){
 37         ll ux=que.front().first,uy=que.front().second;
 38         que.pop();
 39         f(i,0,3){
 40             ll vx=ux+xa[i],vy=uy+ya[i];
 41             if(Map[vx][vy]&&dis[vx][vy]==-1){
 42                 que.push(make_pair(vx,vy));
 43                 dis[vx][vy]=dis[ux][uy]+1;
 44             }
 45         }
 46     }
 47     if(d==5) return;//用于每次处理最少空格单独行走步数
 48     ll num=getnum(a,b);
 49     f(i,0,3){
 50         ll vx=a+xa[i],vy=b+ya[i];
 51         if(dis[vx][vy]>0)
 52             //状态连边
 53             add(num+d,num+i,dis[vx][vy]);
 54     }
 55     //交换位置,getnum表示相对位置取反
 56     add(num+d,getnum(x,y)+fat(d),1);
 57 }
 58 ll far[maxm];
 59 bool vis[maxm];
 60 queue<ll> Q;
 61 il void spfa(ll sx,ll sy){//基本的spfa
 62     memset(far,-1,sizeof(far));//mem-1可以相当于赋值
 63     ll num=getnum(sx,sy);
 64     f(i,0,3){
 65         ll vx=sx+xa[i],vy=sy+ya[i];
 66         if(dis[vx][vy]!=-1){
 67             far[num+i]=dis[vx][vy];
 68             Q.push(num+i);
 69         }
 70     }
 71     //↑压入起始状态(<=4种)
 72     while(!Q.empty()){
 73         ll u=Q.front();
 74         Q.pop();
 75         vis[u]=0;
 76         r(i,u){
 77             ll v=e[i].to;
 78             if(far[v]>far[u]+e[i].w||far[v]==-1){
 79                 far[v]=far[u]+e[i].w;
 80                 if(!vis[v]){
 81                     Q.push(v);
 82                     vis[v]=1;
 83                 }
 84             }
 85         }
 86     }
 87 }
 88 int main()
 89 {
 90     cin>>n>>m>>q;
 91     f(i,1,n) f(j,1,m) cin>>Map[i][j];
 92     f(i,1,n){
 93         f(j,1,m){
 94             if(!Map[i][j]) continue;
 95             f(o,0,3){
 96                 //处理每相邻状态的空格移动的最小步数
 97                 //包括目标点不动空格动(<=3种)，目标空格交换位置(1种)
 98                 ll x=i+xa[o],y=j+ya[o];
 99                 if(Map[x][y]) bfs(i,j,x,y,o);
100             }
101         }
102     }
103     ll sx,sy,ex,ey,tx,ty,ans;
104     while(q--){
105         ans=INF;
106         cin>>ex>>ey>>sx>>sy>>tx>>ty;
107         if(sx==tx&&sy==ty){cout<<0<<endl;continue;}
108         bfs(sx,sy,ex,ey,5);
109         //借用bfs求出空格独立行走最短路
110         spfa(sx,sy);
111         ll num=getnum(tx,ty);
112         f(i,0,3)
113             if(far[num+i]!=-1) ans=min(ans,far[num+i]);
114         cout<<((ans==INF)?-1:ans)<<endl;
115     }
116 }