算法：数字推盘游戏--重排九宫（8-puzzle）

一、数字推盘游戏

　　数字推盘游戏（n-puzzle）是一种最早的滑块类游戏，常见的类型有十五数字推盘游戏和八数字推盘游戏等。也有以图画代替数字的推盘游戏。可能Noyes Palmer Chapman在1874年发明十五数字推盘，但Sam Loyd则在1891年也宣称为其发明。

　　八数字推盘（又名重排九宫）则同样是Noyes Palmer Chapman在1870年代发明，并且马丁·加德纳在科学科普杂志上寻求更快的解答。也有人宣称重排九宫是传统中国游戏，来自洛书，并且为华容道的祖先。

二、分支界定法

　　给定一个具有 8 个图块的 3×3 板（每个图块都有一个 1 到 8 的数字）和一个空白空间（用 0 代表）。目的是将数字放置在图块上，以使用空白的空间匹配最终配置。我们可以将四个相邻的（左，右，上方和下方）图块滑动到空白区域。

　　通常可以使用 DFS、BFS 搜索算法来进行暴力破解。本文利用分支界定法，来“智能”的排名函数（近似于成本函数）来加快对成本节点的搜索，这里每一个节点都存有当前移动后整个方块的分布，从而避免在找不到最终答案的子树继续搜索。

　　分支界定法基本上涉及三种类型的节点：

1. 存活节点，是已生成但尚未生成其子节点的节点；
2. 当前正在扩展的节点，探索它的子节点；
3. 死亡节点，死节点是生成的节点，将不再扩展或探索。死节点的所有子节点均已扩展。

　　成本函数：C(x) = g(x) + h(x)。

　　g(x) 是当前节点到根节点的成本（即路径长度）。h(x) 是当前除开空白块外与答案节点错位（放错位置）的成本，假设在往上下左右任一方向移动图块的成本为 1。　　

　　给定初始状态和目的状态：

　　下图显示了上述算法从给定的8-Puzzle初始配置达到最终配置所遵循的路径。注意，仅具有最小成本函数值的节点被扩展。

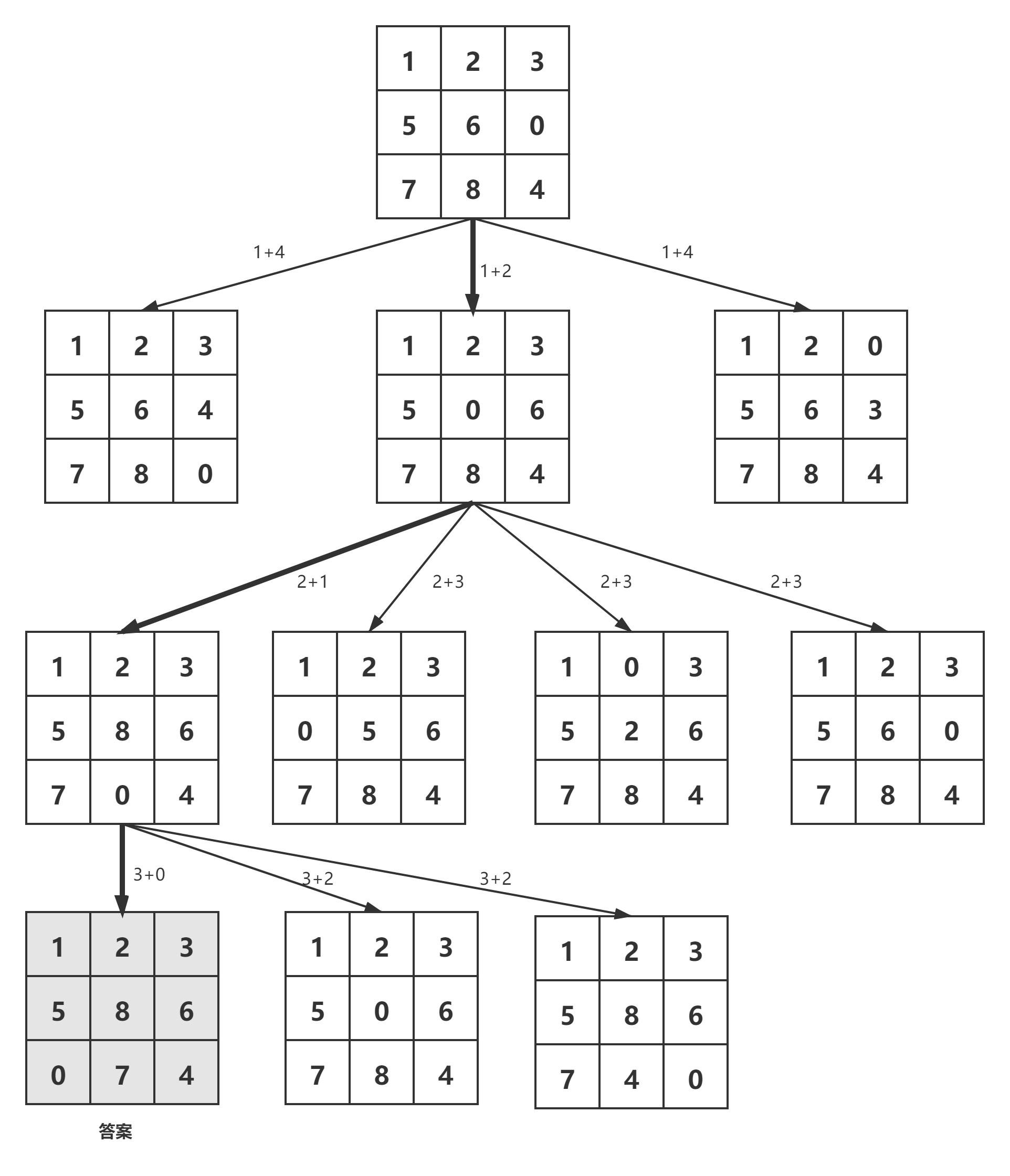
（注意：以上是本算法的流程图）

三、分支界定法的实现

节点的构造：

 1     /**
 2      * 节点
 3      */
 4     private class Node {
 5         private Node parent;
 6         private int[][] mat;
 7         private int x, y;
 8         private int cost;
 9         private int level;
10         private Node() {
11             mat = new int[N][N];
12         }
13     }

插入一个新节点：

 1 　　/**
 2      * 分配一个新节点
 3      *
 4      * @param mat
 5      * @param x
 6      * @param y
 7      * @param newX
 8      * @param newY
 9      * @param level
10      * @param parent
11      * @return
12      */
13     private Node newNode(int[][] mat, int x, int y, int newX, int newY, int level, Node parent) {
14         Node node = new Node();
15         node.parent = parent;
16
17         copyMatrix(mat, node.mat);
18
19         swap(node.mat, x, y, newX, newY);
20
21         node.cost = Integer.MAX_VALUE;
22         node.level = level;
23
24         node.x = newX;
25         node.y = newY;
26
27         return node;
28     }

计算错位成本：

 1     /**
 2      * 计算错位方块的数量, 即不在目标位置的非空白块的数量
 3      *
 4      * @param initial
 5      * @param finals
 6      * @return
 7      */
 8     private int calculateCost(int[][] initial, int[][] finals) {
 9         int count = 0;
10         for (int i = 0; i < N; i++)
11             for (int j = 0; j < N; j++)
12                 if (initial[i][j] != 0 && initial[i][j] != finals[i][j]) {
13                     count++;
14                 }
15         return count;
16     }

利用优先队列（PriorityQueue）来实现分支界定法：

 1     /**
 2      * 分支界定法解决问题
 3      *
 4      * @param initial
 5      * @param x
 6      * @param y
 7      * @param finals
 8      */
 9     private void solve(int[][] initial, int x, int y, int[][] finals) {
10         // 创建优先级队列以存储搜索树的活动节点
11         PriorityQueue<Node> pq = new PriorityQueue<>(new Comp());
12
13         // 创建一个根节点并计算其成本
14         Node root = newNode(initial, x, y, x, y, 0, null);
15         root.cost = calculateCost(initial, finals);
16
17         // 将根添加到活动节点列表中；
18         pq.add(root);
19
20         // 查找成本最低的活动节点，
21         // 将其子级添加到活动节点列表中，并最后将其从列表中删除。
22         while (!pq.isEmpty()) {
23             // 查找估计成本最低的活动节点, 找到的节点将从活动节点列表中删除
24             Node min = pq.poll();
25
26             // 如果min是一个答案节点
27             if (min.cost == 0) {
28                 printPath(min);
29                 return;
30             }
31
32             // 为每个min节点的孩子
33             // 一个节点最多4个孩子
34             for (int i = 0; i < 4; i++) {
35                 if (isSafe(min.x + row[i], min.y + col[i])) {
36                     // 创建一个子节点并计算它的成本
37                     Node child = newNode(min.mat, min.x, min.y,
38                             min.x + row[i], min.y + col[i],
39                             min.level, min);
40                     child.cost = calculateCost(child.mat, finals);
41
42                     // 将min的孩子添加到活动节点列表
43                     pq.add(child);
44                 }
45             }
46         }
47     }

　　分支定界是一种算法设计范例，通常用于解决组合优化问题。 这些问题通常在时间复杂度上呈指数关系（2^N），在最坏的情况下可能需要探索所有可能的排列（扩展完堆中所有可能的节点）。 分支界定相对较快地解决了这些问题。但是在最坏的情况下，我们需要完全计算整个树。充其量，我们只需要完全计算一条穿过树的路径，然后修剪其余路径即可。

本文源代码：

  1 package algorithm;
  2
  3 import java.util.Comparator;
  4 import java.util.PriorityQueue;
  5
  6 /**
  7  * 重排九宫，或者称之为八码数问题，或是说数字推盘问题4，使用分支界定法实现
  8  */
  9 public class EightPuzzle {
 10     // 方阵边长
 11     private static final int N = 3;
 12
 13     // 坐标的行列索引向下、左、上、右
 14     private static final int[] row = {1, 0, -1, 0};
 15     private static final int[] col = {0, -1, 0, 1};
 16
 17     /**
 18      * 节点
 19      */
 20     private class Node {
 21         private Node parent;
 22         private int[][] mat;
 23         private int x, y;
 24         private int cost;
 25         private int level;
 26         private Node() {
 27             mat = new int[N][N];
 28         }
 29     }
 30
 31     /**
 32      * 用于堆排序的比较对象
 33      */
 34     class Comp implements Comparator<Node> {
 35         @Override
 36         public int compare(Node o1, Node o2) {
 37             return (o1.cost + o1.level) - (o2.cost + o2.level);
 38         }
 39     }
 40
 41     /**
 42      * 打印矩阵
 43      *
 44      * @param mat
 45      */
 46     private void printMatrix(int[][] mat) {
 47         for (int i = 0; i < N; i++) {
 48             for (int j = 0; j < N; j++)
 49                 System.out.print(mat[i][j] + " ");
 50             System.out.println();
 51         }
 52     }
 53
 54     /**
 55      * 交换二维矩阵中的值
 56      *
 57      * @param mat
 58      * @param x
 59      * @param y
 60      * @param newX
 61      * @param newY
 62      */
 63     private void swap(int[][] mat, int x, int y, int newX, int newY) {
 64         int tmp = mat[x][y];
 65         mat[x][y] = mat[newX][newY];
 66         mat[newX][newY] = tmp;
 67     }
 68
 69     /**
 70      * 矩阵复制
 71      *
 72      * @param arr1
 73      * @param arr2
 74      */
 75     private static void copyMatrix(int[][] arr1, int[][] arr2) {
 76         for (int i = 0; i < arr1.length; i++)
 77             System.arraycopy(arr1[i], 0, arr2[i], 0, arr1[0].length);
 78
 79     }
 80
 81     /**
 82      * 分配一个新节点
 83      *
 84      * @param mat
 85      * @param x
 86      * @param y
 87      * @param newX
 88      * @param newY
 89      * @param level
 90      * @param parent
 91      * @return
 92      */
 93     private Node newNode(int[][] mat, int x, int y, int newX, int newY, int level, Node parent) {
 94         Node node = new Node();
 95         node.parent = parent;
 96
 97         copyMatrix(mat, node.mat);
 98
 99         swap(node.mat, x, y, newX, newY);
100
101         node.cost = Integer.MAX_VALUE;
102         node.level = level;
103
104         node.x = newX;
105         node.y = newY;
106
107         return node;
108     }
109
110     /**
111      * 计算错位方块的数量, 即不在目标位置的非空白块的数量
112      *
113      * @param initial
114      * @param finals
115      * @return
116      */
117     private int calculateCost(int[][] initial, int[][] finals) {
118         int count = 0;
119         for (int i = 0; i < N; i++)
120             for (int j = 0; j < N; j++)
121                 if (initial[i][j] != 0 && initial[i][j] != finals[i][j]) {
122                     count++;
123                 }
124         return count;
125     }
126
127     /**
128      * 检查（x，y）是否为有效矩阵坐标
129      *
130      * @param x
131      * @param y
132      * @return
133      */
134     private boolean isSafe(int x, int y) {
135         return (x >= 0 && x < N && y >= 0 && y < N);
136     }
137
138     /**
139      * 打印路径
140      *
141      * @param root
142      */
143     private void printPath(Node root) {
144         if (root == null)
145             return;
146         printPath(root.parent);
147         printMatrix(root.mat);
148         System.out.println();
149     }
150
151     /**
152      * 分支界定法解决问题
153      *
154      * @param initial
155      * @param x
156      * @param y
157      * @param finals
158      */
159     private void solve(int[][] initial, int x, int y, int[][] finals) {
160         // 创建优先级队列以存储搜索树的活动节点
161         PriorityQueue<Node> pq = new PriorityQueue<>(new Comp());
162
163         // 创建一个根节点并计算其成本
164         Node root = newNode(initial, x, y, x, y, 0, null);
165         root.cost = calculateCost(initial, finals);
166
167         // 将根添加到活动节点列表中；
168         pq.add(root);
169
170         // 查找成本最低的活动节点，
171         // 将其子级添加到活动节点列表中，并最后将其从列表中删除。
172         while (!pq.isEmpty()) {
173             // 查找估计成本最低的活动节点, 找到的节点将从活动节点列表中删除
174             Node min = pq.poll();
175
176             // 如果min是一个答案节点
177             if (min.cost == 0) {
178                 printPath(min);
179                 return;
180             }
181
182             // 为每个min节点的孩子
183             // 一个节点最多4个孩子
184             for (int i = 0; i < 4; i++) {
185                 if (isSafe(min.x + row[i], min.y + col[i])) {
186                     // 创建一个子节点并计算它的成本
187                     Node child = newNode(min.mat, min.x, min.y,
188                             min.x + row[i], min.y + col[i],
189                             min.level, min);
190                     child.cost = calculateCost(child.mat, finals);
191
192                     // 将min的孩子添加到活动节点列表
193                     pq.add(child);
194                 }
195             }
196         }
197     }
198
199     public static void main(String[] args) {
200         int[][] initial =
201         {
202             {1, 2, 3},
203             {5, 6, 0},
204             {7, 8, 4}
205         };
206
207         int[][] finals =
208         {
209             {1, 2, 3},
210             {5, 8, 6},
211             {0, 7, 4}
212         };
213
214         // 0的位置（空白块）
215         int x = 1, y = 2;
216
217         EightPuzzle eightPuzzle = new EightPuzzle();
218         eightPuzzle.solve(initial, x, y, finals);
219
220     }
221 }