这次不咕了。

首先发现这套题目十分毒瘤， $T1$ 就没有太大的思路。

结果最后也是暴力收场。。。

菜。

$T1\;60pts$ 暴力居然还是挺高的，$T2$ 莽了一个随机化上去结果还是暴力分数。$T3$过于莽撞只打了一个垃得不能再垃的暴力结果只有 $30pts$ ，结果赛后 $set$ 直接撑到 $60pts$。

挂了不少，主要还是欠考虑。

$T1$ 主要就是在 $60pts$ 的基础之上把前缀和优化加上，这样的话就只用处理一个 $\mathcal O(4000^2log(4000))$ 的预处理，因为常数还是比较小的，所以没有什么问题，完全可以跑动。

之后在询问每一个问题的时候，我们只需要输出 $he_{n-1,m-1}*2+n+m$ 就是最终的答案。

$code$:

#include<bits/stdc++.h>

using std::cout; using std::endl;

#define debug cout<<"debug"<<endl

//#define int long long

namespace xin_io

{

	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++

	#define scanf eat1 = scanf

	#define freopen eat2 = freopen

	int eat1; FILE *eat2; char buf[1<<20],*p1 = buf,*p2 = buf;

	inline void openfile() {freopen("t.txt","r",stdin);} inline void outfile() {freopen("o.txt","w",stdout);}

	template<class type>inline type get()

	{

		type s = 0,f = 1; register char ch = gc();

		while(!isdigit(ch)) {if(ch == '-') f = -1; ch = gc();}

		while(isdigit(ch))  {s = s * 10 + ch - '0'; ch = gc();}

		return s * f;

	}

}

using namespace xin_io; static const int maxn = 4e3+10,inf = 0x7f7f7f,mod = (1<<30);

#define try(i,a,b) for(register signed i=a;i<=b;++i)

#define throw(i,a,b) for(register signed i=a;i>=b;--i)

typedef long long ll;

namespace xin

{

	#define max(a,b) (a > b ? a : b)

	int he[maxn][maxn][2],f[maxn][maxn];

	int T,ans = 0;

	inline int gcd(int x,int y)

	{return !y ? x : gcd(y,x%y);}

	inline int gan(int n,int m,int i,int j)

	{

		if(gcd(i,j) == 1)

			return (n - i) * (m - j) - (max(n - (i << 1),0) * (max(m - (j << 1),0)));

		else return 0;

	}

	inline short main()

	{

	#ifndef ONLINE_JUDGE

		openfile();

	#endif

		T = get<signed>();

		try(i,1,4000)

			try(j,1,4000)

			{

				he[i][j][0] = (he[i-1][j][0] + he[i][j-1][0] - he[i-1][j-1][0] + (gcd(i,j) == 1));

				he[i][j][1] = (he[i-1][j][1] + he[i][j-1][1] - he[i-1][j-1][1] - he[i/2][j/2][0] + he[i][j][0]);

				he[i][j][0] &= (mod - 1); he[i][j][1] &= (mod - 1);

			}

		try(que,1,T)

		{

			register int n = get<signed>(),m = get<signed>();

			printf("%d\n",(n + m + 2 * he[n-1][m-1][1]) & (mod - 1));

		}

		return 0;

	}

}

signed main() {return xin::main();}

T2:

$T2$ 到最后还是暴力收场了，用并查集优化也是我没有想到的，思路还是要再宽一点。

我们对于权值进行排序，运用贪心的思想，然后从其中权值最大的开始，把连接他的并且权值比他大的边进行合并就可以，之后开始计算这个联通集合当中的最长路和最长路两端的端点，为什么要计算两端的端点呢？我们就需要知道一个类似性质的东西。

对于合并两个联通集合，其新出现的最长路的端点一定会从两个联通集合原先的最长路的四个端点中选出。

知道这个性质，我们就可以轻松的算出来这个新的联通集合的最长路了。

分 $6$ 种情况讨论。

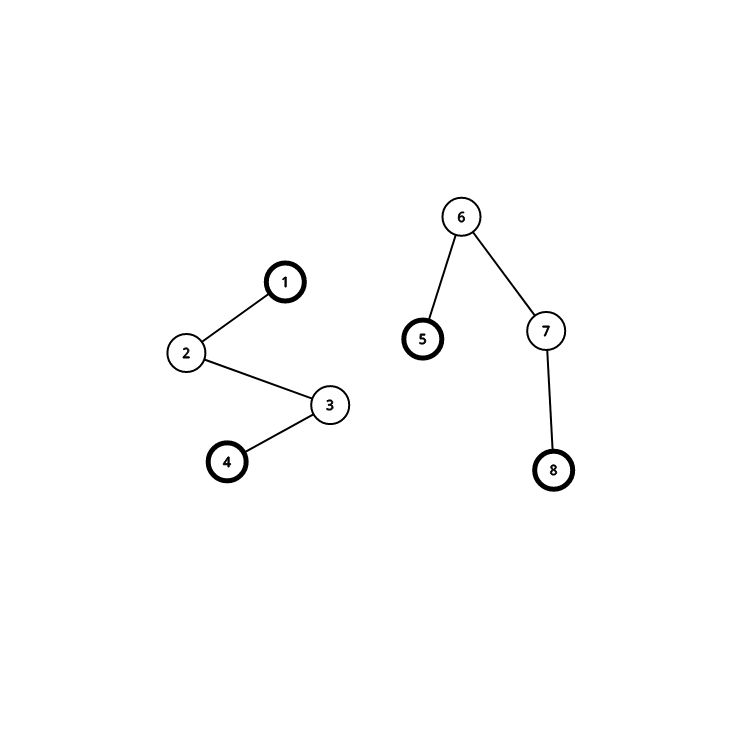
就好比这两个。

1 4
1 5
1 8
4 5
4 8
5 8

分成这六种情况开始计算。之后每次合并更新答案。

$code$:

#include<bits/stdc++.h>

using std::cout; using std::endl;

#define int long long

#define debug cout<<"debug"<<endl

namespace xin_io

{

	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++

	#define scanf eat1 = scanf

	#define freopen eat2 = freopen

	int eat1; FILE *eat2; char buf[1<<20],*p1 = buf,*p2 = buf;

	inline void openfile() {freopen("t.txt","r",stdin);} inline void outfile() {freopen("o.txt","w",stdout);}

	template<class type>inline type get()

	{

		type s = 0,f = 1; register char ch = gc();

		while(!isdigit(ch)) {if(ch == '-') f = -1; ch = gc();}

		while(isdigit(ch))  {s = s * 10 + ch - '0'; ch = gc();}

		return s * f;

	}

}

using namespace xin_io; static const int inf = 0x7f7f7f7f,mod = 998244353;

#define try(i,a,b) for(register signed i=a;i<=b;++i)

#define throw(i,a,b) for(register signed i=a;i>=b;--i)

typedef long long ll;

#define m(c,size) memset(c,0,size)

int n,T;

namespace xin

{

	const int maxn = 1e6+10;

	class xin_edge{public:int next,ver,w;}edge[maxn];

	class xin_data

	{

		public:

			int id,w;

			friend bool operator < (xin_data x,xin_data y)

			{return x.w > y.w;}

	}c[maxn];

	int head[maxn],zhi = 0;

	inline void add(int x,int y,int z) {edge[++zhi].ver = y; edge[zhi].w = z;edge[zhi].next = head[x]; head[x] = zhi;}

/*	inline bool pan(int ci)

	{

		double t = (double)clock() / (double)CLOCKS_PER_SEC;

		if(t > ci * tmax) return false;

		return true;

	}*/

	inline int random(int x) {return (ll) rand() * rand() % x;}

	int top[maxn],size[maxn],hson[maxn],d[maxn],fa[maxn],he[maxn];

	void dfs1(int x,int f)

	{

		d[x] = d[f] + 1; fa[x] = f; size[x] = 1;

		for(register int i=head[x];i;i=edge[i].next)

		{

			register int y = edge[i].ver,z = edge[i].w;

			if(y == f) continue;

			he[y] = he[x] + z;

			dfs1(y,x);

			size[x] += size[y];

			if(size[y] > size[hson[x]]) hson[x] = y;

		}

	}

	void dfs2(int x,int t)

	{

		top[x] = t;

		if(hson[x]) dfs2(hson[x],t);

		for(register int i=head[x];i;i=edge[i].next)

		{

			register int y = edge[i].ver;

			if(y == fa[x] or y == hson[x]) continue;

			dfs2(y,y);

		}

	}

	inline int lca(int x,int y)

	{

		while(top[x] != top[y])

		{

			if(d[top[x]] < d[top[y]]) std::swap(x,y);

			x = fa[top[x]];

		}

		if(d[x] > d[y]) std::swap(x,y);

		return x;

	}

//	void merge(int x,int y) {f[find(y)] = find(x);}

	inline int getdis(int x,int y)

	{

		int nc = lca(x,y);

		return he[x] + he[y] - 2 * he[nc];

	}

	int val[maxn];

	ll ans;

	class xin_bcj

	{

		public:

			int l,r,id,minn;

			ll dis;

			xin_bcj(){}

			xin_bcj(int l,int r,int id,int minn):l(l),r(r),id(id),minn(minn){}

	}bcj[maxn];

	inline int find(int x){return x == bcj[x].id ? bcj[x].id : bcj[x].id = find(bcj[x].id);}

	inline void clear()

	{

		zhi = 0;

		m(head,sizeof(int) * (n+1));

		try(i,1,n)

		{

			edge[i].next = edge[i].ver = edge[i].w = 0;

			bcj[i] = xin_bcj(0,0,0,0);

		}

		m(top,sizeof(int) * (n+1)); m(size,sizeof(int) * (n+1)); m(hson,sizeof(int) * (n+1));

		m(d,sizeof(int) * (n + 1)); m(fa,sizeof(int) * (n + 1));

	}

	inline void merge(int x,int y)

	{

		if(find(x) == find(y)) return ;

		register int fx = find(x),fy = find(y);

		bcj[fx].id = fy; bcj[fy].minn = std::min(bcj[fy].minn,bcj[fx].minn);

		int maxx = -inf,newl,newr;

		register int xl = bcj[fx].l,xr = bcj[fx].r,yl = bcj[fy].l,yr = bcj[fy].r,temp;

		if((temp = getdis(xl,yl)) > maxx) {maxx = temp;newl = xl; newr = yl;}

		if((temp = getdis(xl,yr)) > maxx) {maxx = temp;newl = xl; newr = yr;}

		if((temp = getdis(xr,yl)) > maxx) {maxx = temp;newl = xr; newr = yl;}

		if((temp = getdis(xr,yr)) > maxx) {maxx = temp;newl = xr; newr = yr;}

		if((temp = getdis(xl,xr)) > maxx) {maxx = temp;newl = xl; newr = xr;}

		if((temp = getdis(yl,yr)) > maxx) {maxx = temp;newl = yl; newr = yr;}

		bcj[fy].dis = maxx; bcj[fy].l = newl; bcj[fy].r = newr;

		ans = std::max(ans,1ll * bcj[fy].minn * bcj[fy].dis);

	}

	inline short main()

	{

//	#ifndef ONLINE_JUDGE

//		openfile();

//	#endif

//		srand((unsigned)(time(0)));

//		T = get<signed>();

//		tmax = 2.40 / (T * 1.0);

		try(que,1,T)

		{

			if(que xor 1) clear();

			if(que xor 1) n = get<signed>();

			try(i,1,n) c[i].w = get<signed>(),c[i].id = i,val[i] = c[i].w;

			try(i,1,n) bcj[i].id = bcj[i].l = bcj[i].r = i,bcj[i].minn = val[i];

			try(i,1,n-1)

			{

				register int x = get<signed>(),y = get<signed>(),z = get<signed>();

				add(x,y,z); add(y,x,z);

			}

			dfs1(1,0); dfs2(1,1);std::sort(c+1,c+n+1);

			ans = -inf;

			try(i,1,n)

			{

				register int x = c[i].id;

				for(register int i=head[x];i;i=edge[i].next)

				{

					register int y = edge[i].ver;

					if(val[y] < val[x]) continue;

					merge(x,y);

				}

			}

			cout<<ans<<endl;

		}

		return 0;

	}

}

signed main()

{

#ifndef ONLINE_JUDGE

	openfile();

#endif

	T = get<signed>();	n = get<signed>();

	xin::main();

	return 0;

}

T3:

首先读懂题意，然后发现显然用线段树维护。

然而并不是很好去维护，我们还是需要记录很多变量分很多中情况讨论。

首先提供 $30pts$ 做法：

就是暴力枚举每一个剩下的位置。

然后去寻找那个能离某个花精最远的位置。

然而也并不是很好写。。。。

#include<bits/stdc++.h>

using std::cout; using std::endl;

#define debug cout<<"debug"<<endl

namespace xin_io

{

	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++

	#define scanf eat1 = scanf

	#define freopen eat2 = freopen

	int eat1; FILE *eat2; char buf[1<<20],*p1 = buf,*p2 = buf;

	inline void openfile() {freopen("t.txt","r",stdin);} inline void outfile() {freopen("o.txt","w",stdout);}

	template<class type>inline type get()

	{

		type s = 0,f = 1; register char ch = gc();

		while(!isdigit(ch)) {if(ch == '-') f = -1; ch = gc();}

		while(isdigit(ch))  {s = s * 10 + ch - '0'; ch = gc();}

		return s * f;

	}

}

using namespace xin_io; static const int maxn = 1e6+10,inf = 0x7f7f7f,mod = 998244353;

#define try(i,a,b) for(register signed i=a;i<=b;++i)

#define throw(i,a,b) for(register signed i=a;i>=b;--i)

typedef long long ll;

namespace xin

{

	bool vis[maxn];

	int n,m;

	int head[maxn];

	class xin_data

	{

		public:

			int x,far;

			friend bool operator < (xin_data x,xin_data y)

			{return (x.far == y.far) ? x.x < y.x : x.far > y.far;}

			xin_data(){}

			xin_data(int x,int far):x(x),far(far){}

	};

	std::priority_queue<xin_data>q;

	xin_data que[maxn];int zhi = 0;

	inline int getmax(int pos)

	{

		int r = 0;

		throw(i,n,1) if(vis[i]) {r = i; break;}

		if(!r) {vis[1] = 1; head[pos] = 1; return 1;}

		int far = 0,maxv = -inf,maxp;

		try(i,1,n)

		{

			if(vis[i]) continue;

//			while(!q.empty()) q.pop();

			zhi = 0;

			try(j,0,n)

			{

				if(i + j <= n and vis[i + j]) {que[++zhi] = xin_data(i,j); break;}

				if(i - j >= 1 and vis[i - j]) {que[++zhi] = xin_data(i,j); break;}

//				std::sort(que+1,que+zhi+1);

			}

			int temp = que[zhi].x,away = que[zhi].far;

			if(away > maxv or (away == maxv and temp < maxp))

				maxv = away,maxp = temp;

		}

		vis[maxp] = 1; return head[pos] = maxp;

	}

	inline short main()

	{

	#ifndef ONLINE_JUDGE

		openfile();

	#endif

		n = get<signed>(); m = get<signed>();

		try(que,1,m)

		{

			register int op = get<signed>(),pos = get<signed>();

			if(op == 1)

				printf("%d\n",getmax(pos));

			else

				vis[head[pos]] = false;

		}

		return 0;

	}

}

signed main() {return xin::main();}

对于 $%60$ 的数据：

题解对我发起了挑战，所以我就搞出来了一个能拿到 $60pts$ 的做法

所以以后这个题解该改一改了

用 $set$ 维护之间距离，然后 $iterator$ 遍历取出元素就行了。

#include<bits/stdc++.h>

using std::cout; using std::endl;

#define debug cout<<"debug"<<endl

namespace xin_io

{

	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++

	#define scanf eat1 = scanf

	#define freopen eat2 = freopen

	int eat1; FILE *eat2; char buf[1<<20],*p1 = buf,*p2 = buf;

	inline void openfile() {freopen("t.txt","r",stdin);} inline void outfile() {freopen("o.txt","w",stdout);}

	template<class type>inline type get()

	{

		type s = 0,f = 1; register char ch = gc();

		while(!isdigit(ch)) {if(ch == '-') f = -1; ch = gc();}

		while(isdigit(ch))  {s = s * 10 + ch - '0'; ch = gc();}

		return s * f;

	}

}

using namespace xin_io; static const int maxn = 1e6+10,inf = 0x7f7f7f,mod = 998244353;

#define try(i,a,b) for(register signed i=a;i<=b;++i)

#define throw(i,a,b) for(register signed i=a;i>=b;--i)

typedef long long ll;

namespace xin

{

	std::set<int>s;

	int n,m;

	bool vis[maxn];

	int head[maxn];

	inline int query(int bian)

	{

		if(!s.size()) {vis[1] = 1;s.insert(1); return head[bian] = 1;}

		if(s.size() == 1)

		{

			int pos = *s.begin();

			int r = n - pos,l = pos - 1;

			if(r > l) {s.insert(n); vis[n] = 1; return head[bian] = n;}

			else {s.insert(1); vis[1] = 1; return head[bian] = n;}

		}

		else

		{

			int l_pos = *s.begin(),r_pos = *s.end(),now,last = l_pos;

			int maxv = -inf,maxp;

			std::set<int>::iterator it;

			for(it = s.begin();it != s.end();++it)

			{

//				if(bian == 8) cout<<" *it =  "<<*it<<endl;

				if(*it == l_pos) continue;

				now = (*it - last - 2) / 2;

//				if(bian == 8) cout<<"*it = "<<*it<<" last = "<<last<<" now = "<<now<<endl;

				if(maxv < now and (*it - last - 2) >= 0) {maxv = now; maxp = now + last + 1;/*if(bian == 5) cout<<"maxp = "<<maxp<<endl;*/}

				last = *it;

			}

//			if(bian == 8) cout<<"maxp = "<<maxp<<" maxv = "<<maxv<<" last = "<<last<<" l_pos = "<<l_pos<<endl;

			int l_max = l_pos - 2,r_max = n - last - 1;

//			if(bian == 8) cout<<"l_max = "<<l_max<<" r_max = "<<r_max<<endl;

			if(l_max >= maxv and l_max >= r_max) {s.insert(1); vis[1] = 1; return head[bian] = 1;}

			else

			{

				if(r_max > maxv) {s.insert(n); vis[n] = 1; return head[bian] = n;}

				else {s.insert(maxp); vis[maxp] = 1; return head[bian] = maxp;}

			}

		}

	}

	inline short main()

	{

	#ifndef ONLINE_JUDGE

		openfile();

	#endif

		n = get<signed>(); m = get<signed>();

		try(que,1,m)

		{

			register int op = get<signed>(),bian = get<signed>();

			if(op == 1)

				printf("%d\n",query(bian));

			else vis[bian] = false,s.erase(head[bian]);;

		}

		return 0;

	}

}

signed main() {return xin::main();}

然后就是正解，维护线段树，每次的答案就是 $t[1].ans$

就这样。

只不过要写一堆东西，说也说不清，所以看代码就行了。。。。。

#include<bits/stdc++.h>

using std::cout; using std::endl;

#define debug cout<<"debug"<<endl

namespace xin_io

{

	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++

	#define scanf eat1 = scanf

	#define freopen eat2 = freopen

	int eat1; FILE *eat2; char buf[1<<20],*p1 = buf,*p2 = buf;

	inline void openfile() {freopen("t.txt","r",stdin);} inline void outfile() {freopen("o.txt","w",stdout);}

	template<class type>inline type get()

	{

		type s = 0,f = 1; register char ch = gc();

		while(!isdigit(ch)) {if(ch == '-') f = -1; ch = gc();}

		while(isdigit(ch))  {s = s * 10 + ch - '0'; ch = gc();}

		return s * f;

	}

}

using namespace xin_io; static const int maxn = 1e6+10,inf = 0x7f7f7f,mod = 998244353;

#define try(i,a,b) for(register signed i=a;i<=b;++i)

#define throw(i,a,b) for(register signed i=a;i>=b;--i)

typedef long long ll;

namespace xin

{

	int n,m;

	class xin_segment

	{

		private:

			#define ls(fa) (fa << 1)

			#define rs(fa) (fa << 1 | 1)

			inline void up(int fa,int l,int r)

			{

				t[fa].mid_mid_val = t[ls(fa)].mid_mid_val; t[fa].l_l_mid_val = t[ls(fa)].l_l_mid_val; t[fa].r_r_mid_val = t[ls(fa)].r_r_mid_val;

				if(((t[fa].mid_mid_val + 1) >> 1) < ((t[rs(fa)].l_mid_val + t[ls(fa)].r_mid_val + 1) >> 1))

					t[fa].mid_mid_val = t[rs(fa)].l_mid_val + t[ls(fa)].r_mid_val,t[fa].l_l_mid_val = t[ls(fa)].l_r_val,t[fa].r_r_mid_val = t[rs(fa)].r_l_val;

				if(((t[fa].mid_mid_val + 1) >> 1) < ((t[rs(fa)].mid_mid_val + 1) >> 1))

					t[fa].mid_mid_val = t[rs(fa)].mid_mid_val,t[fa].l_l_mid_val = t[rs(fa)].l_l_mid_val,t[fa].r_r_mid_val = t[rs(fa)].r_r_mid_val;

//				cout<<"t[rs(fa)].l_l_mid_val = "<<t[rs(fa)].l_l_mid_val<<endl;

				register int mid = l + r >> 1;

				t[fa].l_mid_val = t[ls(fa)].l_mid_val; t[fa].r_l_val = t[ls(fa)].r_l_val;

				if(t[fa].l_mid_val == mid + 1 - l) t[fa].l_mid_val += t[rs(fa)].l_mid_val,t[fa].r_l_val = t[rs(fa)].r_l_val;

				t[fa].r_mid_val = t[rs(fa)].r_mid_val; t[fa].l_r_val = t[rs(fa)].l_r_val;

				if(t[fa].r_mid_val == r - mid) t[fa].r_mid_val += t[ls(fa)].r_mid_val,t[fa].l_r_val = t[ls(fa)].l_r_val;

			}

		public:

			class xin_tree{public:int mid_mid_val,l_l_mid_val,r_r_mid_val,l_mid_val,r_mid_val,r_l_val,l_r_val;}t[maxn];

			inline void build(int fa,int l,int r)

			{

				t[fa].l_mid_val = t[fa].r_mid_val = t[fa].mid_mid_val = r - l + 1;

				t[fa].l_l_mid_val = t[fa].l_r_val = l; t[fa].r_l_val = t[fa].r_r_mid_val = r;

				if(l == r) return ;

				register int mid = l + r >> 1;

				build(ls(fa),l,mid); build(rs(fa),mid+1,r);

				up(fa,l,r);

			}

			inline void modify(int fa,int l,int r,int pos,int val)

			{

				if(pos > r or pos < l )return;

				if(l == r)

				{

					if(val == 2) t[fa].mid_mid_val = t[fa].l_mid_val = t[fa].r_mid_val = 1,t[fa].l_l_mid_val = t[fa].r_r_mid_val = t[fa].l_r_val = t[fa].r_l_val = pos;

					else t[fa].mid_mid_val = t[fa].l_mid_val = t[fa].r_mid_val = 0,t[fa].l_l_mid_val = t[fa].l_r_val = pos + 1,t[fa].r_r_mid_val = t[fa].r_l_val = pos - 1;

					return ;

				}

				register int mid = l + r>> 1;

				modify(ls(fa),l,mid,pos,val); modify(rs(fa),mid+1,r,pos,val);

				up(fa,l,r);

			}

	}t;

	int head[maxn];

	inline short main()

	{

	#ifndef ONLINE_JUDGE

		openfile();

	#endif

		n = get<signed>(); m = get<signed>();

		t.build(1,1,n);

		try(i,1,m)

		{

			register int op = get<signed>(),bian = get<signed>();

			if(op == 2)

				t.modify(1,1,n,head[bian],2);

			else

			{

				int pos = (t.t[1].r_r_mid_val + t.t[1].l_l_mid_val) >> 1;

				if(t.t[1].l_l_mid_val == 1 or t.t[1].l_mid_val >= (t.t[1].mid_mid_val + 1) >> 1) pos = 1;

				else if(t.t[1].r_r_mid_val == n or t.t[1].r_mid_val > (t.t[1].mid_mid_val + 1) >> 1) pos = n;

				printf("%d\n",pos);

//				cout<<"pos = "<<pos<<endl;

				t.modify(1,1,n,pos,1);

				head[bian] = pos;

			}

		}

		return 0;

	}

}

signed main() {return xin::main();}

[考试总结]noip模拟15的更多相关文章

6.17考试总结(NOIP模拟8)[星际旅行·砍树·超级树·求和]
6.17考试总结(NOIP模拟8) 背景考得不咋样,有一个非常遗憾的地方:最后一题少取膜了,$100pts->40pts$,改了这么多年的错还是头一回看见以下的情景... T1星际旅行前 ...
5.23考试总结(NOIP模拟2)
5.23考试总结(NOIP模拟2) 洛谷题单看第一题第一眼,不好打呀;看第一题样例又一眼,诶,我直接一手小阶乘走人然后就急忙去干T2T3了后来考完一看,只有$T1$骗到了$15pts$[ ...
5.22考试总结(NOIP模拟1)
5.22考试总结(NOIP模拟1) 改题记录 T1 序列题解暴力思路很好想,分数也很好想$QAQ$ (反正我只拿了5pts) 正解的话: 先用欧拉筛把1-n的素数筛出来 void get_Pr ...
2021.9.17考试总结[NOIP模拟55]
有的考试表面上自称NOIP模拟,背地里却是绍兴一中NOI模拟吓得我直接文件打错 T1 Skip 设状态$f_i$为最后一次选$i$在$i$时的最优解.有$f_i=max_{j<i}[f_j+a ...
[考试总结]noip模拟23
因为考试过多,所以学校的博客就暂时咕掉了,放到家里来写不过话说,vscode的markdown编辑器还是真的很好用先把 $noip$ 模拟 $23$ 的总结写了吧.. 俗话说:" ...
2021.7.15考试总结[NOIP模拟16]
ZJ模拟D2就是NB.. T1 Star Way To Heaven 谁能想到这竟是个最小生成树呢?(T1挂分100的高人JYF就在我身边把上边界和下边界看成一个点和星星跑最小生成树,从上边界开始跑 ...
7.15考试总结(NOIP模拟16)[Star Way To Heaven·God Knows·Lost My Music]
败者死于绝望,胜者死于渴望. 前言一看这个题就来者不善,对于第一题第一眼以为是一个大模拟,没想到是最小生成树. 对于第二题,先是看到了状压可以搞到的 20pts 然后对着暴力一顿猛调后来发现是题面理 ...
2021.8.15考试总结[NOIP模拟40]
T1 送花线段树.枚举右端点,线段树记录左端点对应的值. 每次对当前颜色上上次出现的位置到上次出现的位置区间减,上次出现的位置到当前位置区间加. $code:$ 1 #include<bits ...
2021.10.15考试总结[NOIP模拟77]
$n=40$考虑$meet \;in \;the \;middle$ 某个元素有关的量只有一个时考虑转化为树上问题对暴力有自信,相信数据有梯度没了 UPD:写了个略说人话的. T1 最大或 ...

随机推荐

Halcon 纹理缺陷检测 apply_texture_inspection_model
在纹理中找瑕疵.基于高斯混合模型(GMM)分类器的纹理检查模型,适用于图像金字塔,可以分析纹理的多个频率范围. [要求]训练样本,必须完美无瑕疵. [步骤] 1.创建模型 create_texture ...
Mysql数据库值的添加、修改、删除及清空
3.MySQL数据管理第一种方式:不太建议,看起来复杂些 -- 学生表的 gradeid 字段,要去引用年级表的 gradeid -- 定义外键key -- 给这个外键添加约束,(执行引用),RE ...
【NX二次开发】点到矢量或直线的垂点
已知p1.p2.v1求p0 求解: 通过P1点和P2点,先求出v2: 使用 UF_VEC3_dot(),v1点乘v2得到P0与P2之间的距离: 使用UF_VEC3_unitize()将v1单位化: p ...
JVM调优的反思与总结
垃圾回收的悖论所谓"成也萧何败萧何".Java的垃圾回收确实带来了很多好处,为开发带来了便利.但是在一些高性能.高并发的情况下,垃圾回收确成为了制约Java应用的瓶颈.目前JDK ...
《手把手教你》系列基础篇之（二）-java+ selenium自动化测试-环境搭建（下）基于Maven（详细教程）
1.简介 Apache Maven是一个软件项目管理和综合工具.基于项目对象模型(POM)的概念,Maven可以从一个中心资料片管理项目构建,报告和文件.由于现在企业和公司中Java的大部分项目都是基 ...
C++ 11 关键字
1.auto 我现在用auto,基本是在变量定义时根据初始化表达式自动推断该变量的类型. 另外与关键字 decltype 连用,在声明或定义函数时作为函数返回值的占位符. auto不能用来声明函数的返 ...
Centos 8 误删/boot文件夹下文件后的恢复
一.环境 Centos8 二.过程 1.查看/boot底下文件 ls /boot 2.模拟误删/boot底下文件 rm -rf /boot/*ls /boot 3.reboot,无法正常启动 4.在v ...
Linux搭建私有yum源
一.前期准备环境:CentOS 8.3 镜像: CentOS-7-x86_64-Everything-2009.iso CentOS-8.3.2011-x86_64-dvd1.iso 二.搭建步骤 ...
SpringMVC（7）格式化显示
在SpringMVC(六)数据验证中我们介绍了如何验证提交的数据的正确性,当数据验证通过后就会被我们保存起来.保存的数据会用于以后的展示,这才是保存的价值.那么在展示的时候如何按照要求显示?(比如:小 ...
在Xshell中文件内容显示乱码
1.修改系统语言支持中文 echo $LANG 查看系统语言默认 en_US.UFT_8 vim /etc/locale.conf 修改配置文件将LANG的值改为 zh_CN.UT ...

[考试总结]noip模拟15

T2:

T3:

[考试总结]noip模拟15的更多相关文章

随机推荐

热门专题