「算法笔记」Splay

一、简介

Splay（伸展树）是平衡树中的一种。它通过不断将某个节点旋转到根节点的位置，使整棵树仍满足 BST 的性质，并且保持平衡而不至于退化为链。

频繁访问的节点会被移动到离根节点较近的位置，进而获得更快的访问速度。

可以通过均摊复杂度证明，\(n\) 个点，进行 \(m\) 次 Splay 操作，最终的时间复杂度是 \(\mathcal{O}((n+m)\log n)\)。证明。

二、基本操作

一些维护的信息：

\(rt\)	\(tot\)	\(fa(x)\)	\(lc(x)\)	\(rc(x)\)	\(val(x)\)	\(cnt(x)\)	\(sz(x)\)
根节点编号	节点个数	父亲	左儿子	右儿子	节点权值	权值出现次数	子树大小

基本操作：

• \(\text{getnew}(k)\)：新建一个关键码（即节点权值）为 \(k\) 的节点。

• \(\text{upd}(x)\)：更新节点 \(x\) 的 \(sz\)。

int getnew(int k){
    val[++tot]=k,cnt[tot]=sz[tot]=1;
    return tot;
}
void upd(int p){
    sz[p]=sz[lc[p]]+sz[rc[p]]+cnt[p];
}

三、旋转操作

为了使 Splay 保持平衡而进行旋转操作，旋转的本质是将某个节点上移一个位置。

旋转需要保证：

• 整棵树的中序遍历不变（不能破坏二叉查找树的性质）。

• 受影响的节点维护的信息依然正确有效。

• root​ 必须指向旋转后的根节点。

和 Treap 的旋转操作差不多，只是多了对 \(fa\) 数组的维护。接下来对 Treap 中的旋转操作进行搬运、修改和补充（可能会有锅 QAQ）。

1. 左旋与右旋

在 Splay 中的旋转分为两种：左旋 和 右旋。

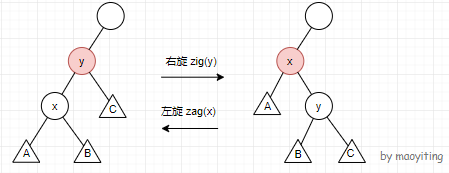
以右旋为例。如图所示，在初始情况下，\(x\) 是 \(y\) 的左子节点，\(A\) 和 \(B\) 分别是 \(x\) 的左右子树，\(C\) 是 \(y\) 的右子树。

“右旋”操作在保持 BST 性质的基础上，把 \(x\) 变为 \(y\) 的父节点。因为 \(x\) 的关键码小于 \(y\) 的关键码，所以 \(y\) 应该作为 \(x\) 的右子节点。

当 \(x\) 变成 \(y\) 的父节点后， \(y\) 的左子树就空了出来，于是 \(x\) 原来的右子树 \(B\) 就恰好作为 \(y\) 的左子树。

• 左旋：将右儿子提到当前节点，自己作为右儿子的左儿子，右儿子原来的左儿子变成自己新的右儿子。

• 右旋：将左儿子提到当前节点，自己作为左儿子的右儿子，左儿子原来的右儿子变成自己新的左儿子。

右旋将左儿子上移，左旋将右儿子上移。左右旋并 没有本质区别。其目的相同，即将指定节点上移一个位置。

2. 代码实现

在之前 Treap 代码上的修改：

• 之前的 Treap 没有记录父节点，方便起见，把左右旋定义为一个节点的子节点绕其向左或向右旋转。（某些书籍中不是这样的）

• 这里的 Splay 记录了父节点，把左右旋定义为一个节点绕其父节点向左或向右旋转。（当然要跟之前 Treap 一样也可以，Code）

• Splay 需要维护 \(fa\) 数组。

具体步骤： （假设需要旋转的节点为 \(x\)，其父亲为 \(y\)，以右旋为例）

1. 将 \(y\) 的左儿子指向 \(x\) 的右儿子，且 \(x\) 的右儿子的父亲指向 \(y\)。

2. 将 \(x\) 的右儿子指向 \(y\)，且 \(y\) 的父亲指向 \(x\)。

3. 如果原来的 \(y\) 还有父亲 \(z\)，那么把 \(z\) 的某个儿子（原来 \(y\) 所在的儿子位置）指向 \(x\)，且 \(x\) 的父亲指向 \(z\)。

void zig(int &p){    //Treap 右旋
    int q=lc[p];
    lc[p]=rc[q],rc[q]=p,p=q,upd(rc[p]),upd(p);
}
void zig(int p){    //Splay 右旋。p 不需要引用。
    int q=fa[p],k=fa[q];
    lc[q]=rc[p],fa[rc[p]]=q;
    rc[p]=q,fa[q]=p,fa[p]=k;
    if(q==lc[k]) lc[k]=p;    //如果原来的 q 还有父亲 k，那么把 k 的某个儿子（原来 q 所在儿子的位置）指向 p。前面已将 p 的父亲指向 q。
    else if(q==rc[k]) rc[k]=p;
    upd(q),upd(p);    //先更新 q 再更新 p
    if(rt==q) rt=p;    //如果原来 q 是根，那么现在 p 就是根
}

Splay 左右旋：（换了个变量名 233）

void zig(int x){    //右旋
    int y=fa[x],z=fa[y];
    lc[y]=rc[x],fa[rc[x]]=y;
    rc[x]=y,fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    upd(y),upd(x);
    if(rt==y) rt=x;
}
void zag(int x){    //左旋
    int y=fa[x],z=fa[y];
    rc[y]=lc[x],fa[lc[x]]=y;
    lc[x]=y,fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    upd(y),upd(x);
    if(rt==y) rt=x;
}

四、伸展操作

Splay 利用伸展操作趋近平衡。具体描述为，将当前访问过的节点旋转至根节点的位置。（伸展操作也称 Splay 操作）

这样旋转的好处在于，经常访问的节点访问速度将速度很快（因为就在根结点附近），而且在旋转的过程中，整棵树也会逐渐平衡。

单旋：反复旋转 \(x\) 的父节点直到 \(x\) 到达根节点为止。使用这种方法，复杂度无法保证，会退化。

双旋：讨论 \(x\) 和父亲的关系 与 \(x\) 的父亲和祖父的关系是否相同。

双旋操作

设访问过的节点为 \(x\)。分三种情况考虑，直到 \(x\) 成为根节点。

情况一： \(fa(x)\) 为根节点。则将 \(x\) 旋转一次到根即可。举个栗子：

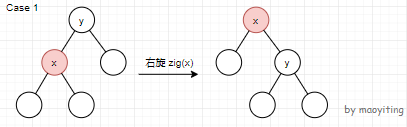
情况二：\(fa(x)\) 不是根节点，\(x\) 是 \(fa(x)\) 的左(右)儿子且 \(fa(x)\) 是 \(fa(fa(x))\) 的左(右)儿子。则先右(左)旋 \(fa(x)\)，再右(左)旋 \(x\) 。栗子：

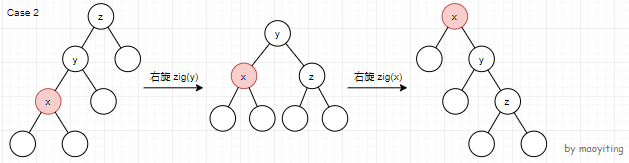
情况三：\(y\) 不是根节点，\(x\) 是 \(fa(x)\) 的左(右)儿子且 \(fa(x)\) 是 \(fa(fa(x))\) 的右(左)儿子。则先右(左)旋 \(x\)，再左(右)旋 \(x\) 。栗子：

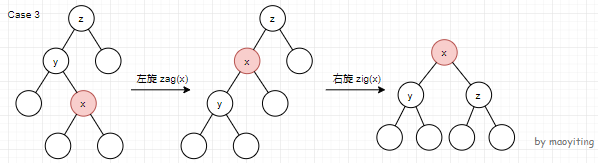
\(\text{Splay(x,g)}\) 表示把 \(x\) 旋转到 \(g\) 的儿子（当 \(g=0\) 时表示旋转到根）。

void rotate(int x){    //通过旋转把节点 x 上移
    int y=fa[x];
    if(x==lc[y]) zig(x);
    else zag(x);
}
void splay(int x,int g){    //把 x 旋转到 g 的儿子的位置（当 g=0 时表示旋转到根）
    while(fa[x]!=g){
        int y=fa[x],z=fa[y];
        if(z!=g) rotate((x==lc[y])==(y==lc[z])?y:x);
        rotate(x);
    }
    if(!g) rt=x;    //标记根节点
}

五、其他操作

1. 查找操作

在 Splay 中查找一个值就需要查找操作。

跟 BST 的查找过程一样，每次根据待查找的值 \(k\) 与当前节点的值的关系，来判断进入左、右儿子。

不过它不会给出返回值，而是把查找到的 \(k\) 对应的节点（若没有找到，就是离 \(k\) 最近的节点）通过 Splay 操作旋转到根节点。

void find(int k){
    if(!rt) return ;    //树是空的就返回
    int x=rt,y;
    while(val[x]!=k&&(y=k<val[x]?lc[x]:rc[x])) x=y;
    splay(x,0);    //伸展到根节点
}

2. 插入操作

按照二叉查找树的性质向下查找，找到待插入的值 \(k\) 应该插入的节点并插入。如果 \(k\) 原来就存在，那么直接更新 \(cnt\)，否则新建一个空节点。

最后把插入的 \(k\) 对应的节点通过 Splay 操作到根节点。

void insert(int k){
    int x=rt,y=0;    //y 是 x 的父节点
    while(x&&val[x]!=k) y=x,x=k<val[x]?lc[x]:rc[x];
    if(x) cnt[x]++;    //找到 k
    else x=getnew(k),y?(k<val[y]?lc[y]=x:rc[y]=x):0,fa[x]=y;    //更新 x 的信息
    splay(x,0);    //伸展到根节点
}

3. 查询排名

\(k\) 的排名定义为第一个等于 \(k\) 的值的排名。

只需把 \(k\) 旋转到根节点，返回根的左子树的 \(sz\) 再加 \(1\) 即可。

（代码中没有加 \(1\) 的原因：为了避免越界，减少边界情况的判断，我们在初始时额外插入了关键码为 \(+\infty\) 和 \(−\infty\) 的节点。所以代码中是不用 \(+1\) 的）

int rank(int k){
    find(k);
    return sz[lc[rt]];
}

4. 第 k 小数

设 \(rk\) 为剩余排名，具体步骤如下：

• 如果 \(rk\) 大于左子树大小与当前节点大小的和，那么向右子树查找。

• 如果 \(rk\) 不大于左子树的大小，那么向左子树查找。

• 否则直接返回当前节点的值。

int Kth(int rk){
    int x=rt;rk++;     //rk+1 是因为有关键码为负无穷大的节点
    while(1){
        if(rk>sz[lc[x]]+cnt[x]) rk-=sz[lc[x]]+cnt[x],x=rc[x];    //右子树
        else if(rk<=sz[lc[x]]) x=lc[x];    //左子树
        else return val[x];
    }
}

5. 查询前驱/后继

前驱定义为小于 \(k\) 且最大的数，后继定义为大于 \(k\) 且最小的数。

查询前驱：将 \(k\) 旋转到根节点， 前驱即为 \(k\) 的左子树中最右边的节点。注意当 \(k\) 不存在时，根节点的值比 \(k\) 小的情况要特判。

查询后继：同理，找 \(k\) 的右子树中最左边的节点即可。

int pre(int k){    //查询前驱
    find(k);
    if(val[rt]<k) return rt;
    int x=lc[rt];
    while(rc[x]) x=rc[x];
    return x;    //这里返回了节点编号，因为后面的删除操作需要用到前驱的编号
}
int nxt(int k){    //查询后继
    find(k);
    if(val[rt]>k) return rt;
    int x=rc[rt];
    while(lc[x]) x=lc[x];
    return x;
}

6. 删除操作

\(\text{splay}(x,g)\) 的 \(g\) 参数就是这里用哒。

删除关键码为 \(k\) 的节点。步骤如下：

• 首先找到 \(k\) 的前驱 \(last\) 和后继 \(next\)。将 \(last\) 旋转到根节点，将 \(next\) 旋转到 \(last\) 的儿子（显然是右儿子）。

• 观察这个过程可以发现：若 \(k\) 存在，那么这时的 \(k\) 一定是 \(next\) 的左儿子，且 \(k\) 对应的节点没有儿子。将这个节点的 \(cnt\) 减 \(1\)（需要 Splay 操作），或者直接删除即可。

void erase(int k){
    int p1=pre(k),p2=nxt(k);    //找到前驱后继
    splay(p1,0),splay(p2,p1);    //把前驱伸展到根结点，把后继伸展到前驱的子节点
    int x=lc[p2];    //这时的 k 一定是该后继的左子结点，且这个节点 x 没有子节点
    if(cnt[x]>1) cnt[x]--,splay(x,0);    //cnt-=1，将 x 伸展到根节点
    else lc[p2]=0;    //删除节点 x
} 

六、模板

禁止某莱白嫖板子

//Luogu P3369
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,opt,x,tot,rt,lc[N],rc[N],val[N],sz[N],cnt[N],fa[N],ans;
void upd(int p){
    sz[p]=sz[lc[p]]+sz[rc[p]]+cnt[p];
}
int getnew(int k){
    val[++tot]=k,cnt[tot]=sz[tot]=1;
    return tot;
}
void zig(int x){    //右旋
    int y=fa[x],z=fa[y];
    lc[y]=rc[x],fa[rc[x]]=y,rc[x]=y,fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    upd(y),upd(x);
    //if(rt==y) rt=x; 这一步在 splay 操作的末尾有，可以省略
}
void zag(int x){    //左旋
    int y=fa[x],z=fa[y];
    rc[y]=lc[x],fa[lc[x]]=y,lc[x]=y,fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    upd(y),upd(x);
    //if(rt==y) rt=x;
}
void rotate(int x){
    x==lc[fa[x]]?zig(x):zag(x);
}
void splay(int x,int g){
    while(fa[x]!=g){
        int y=fa[x],z=fa[y];
        if(z!=g) rotate((x==lc[y])==(y==lc[z])?y:x);
        rotate(x);
    }
    if(!g) rt=x;
}
void find(int k){
    if(!rt) return ;
    int x=rt,y;
    while(val[x]!=k&&(y=k<val[x]?lc[x]:rc[x])) x=y;
    splay(x,0);
}
void insert(int k){
    int x=rt,y=0;
    while(x&&val[x]!=k) y=x,x=k<val[x]?lc[x]:rc[x];
    if(x) cnt[x]++;
    else x=getnew(k),y?(k<val[y]?lc[y]=x:rc[y]=x):0,fa[x]=y;
    splay(x,0);
}
int rank(int k){
    find(k);
    return sz[lc[rt]];
}
int Kth(int rk){
    int x=rt;rk++;
    while(1){
        if(rk>sz[lc[x]]+cnt[x]) rk-=sz[lc[x]]+cnt[x],x=rc[x];
        else if(rk<=sz[lc[x]]) x=lc[x];
        else return val[x];
    }
}
int pre(int k){
    find(k);
    if(val[rt]<k) return rt;
    int x=lc[rt];
    while(rc[x]) x=rc[x];
    return x;
}
int nxt(int k){
    find(k);
    if(val[rt]>k) return rt;
    int x=rc[rt];
    while(lc[x]) x=lc[x];
    return x;
}
void erase(int k){
    int p1=pre(k),p2=nxt(k);
    splay(p1,0),splay(p2,p1);
    int x=lc[p2];
    if(cnt[x]>1) cnt[x]--,splay(x,0);
    else lc[p2]=0;
}
signed main(){
    scanf("%lld",&n),insert(-1e18),insert(1e18);
    while(n--){
        scanf("%lld%lld",&opt,&x),ans=-1;
        if(opt==1) insert(x);
        else if(opt==2) erase(x);
        else if(opt==3) ans=rank(x);
        else if(opt==4) ans=Kth(x);
        else if(opt==5) ans=val[pre(x)];
        else ans=val[nxt(x)];
        if(~ans) printf("%lld\n",ans);
    }
    return 0;
}

附：快乐压行

void rotate(int x){
    int y=fa[x],z=fa[y];
    if(x==lc[y]) lc[y]=rc[x],fa[rc[x]]=y,rc[x]=y;    //zig(x)
    else rc[y]=lc[x],fa[lc[x]]=y,lc[x]=y;    //zag(x)
    fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    upd(y),upd(x);
}

七、维护区间

以 Luogu P3391 文艺平衡树 为例：维护一个有序数列，支持 区间翻转。

总体思路：用 Splay 维护这个序列，节点的关键码为每个数在原数列中的 下标。显然一个子树对应一个区间。每次提取区间 \([l,r]\) 就可以将左右子树全部交换，就实现了区间翻转。

（平衡树上的每个节点存 \(1,2,\cdots,n\)。如果不进行翻转操作的话，这个平衡树在任意时刻，无论经过了多少次 Splay 操作，它的中序遍历都是 \(1,2,\cdots,n\) 这个序列，并且容易发现，一个子树，一定是连续的一段区间。）

提取区间：对于区间 \([l,r]\)，我们可以把 \(l-1\) 旋转到根，\(r+1\) 旋转到根的儿子（显然是右儿子）。那么 根的右儿子的左子树 就是区间 \([l,r]\) 的全部元素。

注意这里的 \(l-1\) 和 \(r+1\) 指的是序列中第 \(l-1\) 和第 \(r+1\) 个元素对应的节点（即平衡树中序遍历的第 \(l-1\) 和第 \(r+1\) 个节点），而不是下标为 \(l-1\) 和 \(r+1\) 的节点。因此我们要调用 Kth(l-1) 和 Kth(r+1) 找到对应节点的编号。

交换子树：加一个 \(\text{tag}\) 标记就好啦，作用就跟线段树的懒标记差不多。每次维护的时候，将标记下传、交换左右子树、清空自身标记。

时间复杂度：\(\mathcal{O}(n\log n)\)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,m,l,r,tot,rt,lc[N],rc[N],val[N],sz[N],cnt[N],fa[N],tag[N],ans;
int getnew(int k){
    val[++tot]=k,cnt[tot]=sz[tot]=1;
    return tot;
}
void pushup(int p){
    sz[p]=sz[lc[p]]+sz[rc[p]]+cnt[p];
}
void pushdown(int p){
    if(!tag[p]) return ;
    swap(lc[p],rc[p]),tag[lc[p]]^=1,tag[rc[p]]^=1,tag[p]=0;
}
void zig(int x){    //右旋
    int y=fa[x],z=fa[y];
    lc[y]=rc[x],fa[rc[x]]=y,rc[x]=y,fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    pushup(y),pushup(x);
}
void zag(int x){    //左旋
    int y=fa[x],z=fa[y];
    rc[y]=lc[x],fa[lc[x]]=y,lc[x]=y,fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    pushup(y),pushup(x);
}
void rotate(int x){
    x==lc[fa[x]]?zig(x):zag(x);
}
void splay(int x,int g){
    while(fa[x]!=g){
        int y=fa[x],z=fa[y];
        if(z!=g) rotate((x==lc[y])==(y==lc[z])?y:x);
        rotate(x);
    }
    if(!g) rt=x;
}
void insert(int k){
    int x=rt,y=0;
    while(x&&val[x]!=k) y=x,x=k<val[x]?lc[x]:rc[x];
    if(x) cnt[x]++;
    else x=getnew(k),y?(k<val[y]?lc[y]=x:rc[y]=x):0,fa[x]=y;
    splay(x,0);
}
int Kth(int rk){
    int x=rt;rk++;
    while(1){
        pushdown(x);
        if(rk>sz[lc[x]]+cnt[x]) rk-=sz[lc[x]]+cnt[x],x=rc[x];
        else if(rk<=sz[lc[x]]) x=lc[x];
        else return x;
    }
}
void rev(int l,int r){
    splay(Kth(l-1),0),splay(Kth(r+1),rt);
    tag[lc[rc[rt]]]^=1;
}
signed main(){
    scanf("%lld%lld",&n,&m),insert(-1e18),insert(1e18);
    for(int i=1;i<=n;i++) insert(i);
    for(int i=1;i<=m;i++)
        scanf("%lld%lld",&l,&r),rev(l,r);
    for(int i=1;i<=n;i++)
        printf("%lld%c",val[Kth(i)],i==n?'\n':' ');
    return 0;
}

关于“翻转操作”是否改变 BST 性质的一些解释：（开始瞎编）

• 从表面上看，交换左右儿子，相当于打乱了关键码的排列方式，破坏了 BST 的性质。

• 事实上，它并没有破坏 BST 的性质。我们需要保证平衡树的中序遍历，就是我们 想要的序列（即经过翻转操作后的序列）。区间翻转时，我们想要的那个序列变了，所以要交换节点。可以理解为，在执行区间翻转时，把 < 号的定义改变了，所以 BST 的结构要做相应的变化，才能维持它 BST 的性质。而这个 < 号的定义，就是它在我们 想要的序列 中的出现位置。（即每个数在我们想要的序列中的出现位置仍满足 BST 性质）

这时的 Kth(rk) 可以理解为是平衡树中序遍历的第 \(rk\) 个数，也就是我们想要的序列里面的第 \(rk\) 个数。

八、Treap 和 Splay 的适用范围

Treap 用于维护集合的信息，支持排名相关的操作，优点是简单易写（相对其他平衡树而言），而且常数较小。

Splay 常数较大且没有那么好写，但是 Splay 能够支持普通 Treap 无法完成的序列操作，一般用于维护动态序列操作。

补充：Treap 还有一种非旋转的实现（核心操作为分裂与合并），可以支持 Splay 的所有操作，还可以 Splay 不支持的可持久化。

九、习题

模板题就不放了叭 QAQ

• Luogu P1486 [NOI2004] 郁闷的出纳员（Code）
• Luogu P2596 [ZJOI2006] 书架（Code）
• Luogu P3224 [HNOI2012] 永无乡（并查集 + 平衡树启发式合并，Code）
• Luogu P1110 [ZJOI2007] 报表统计（线段树 + 平衡树，Code）
• Luogu P2042 [NOI2005] 维护数列（练手题，听说写完这个题就会写一堆动态序列操作的裸题了！打标记 + 内存回收，Code）
• BZOJ 2827 千山鸟飞绝（map + 打标记，Code）
• BZOJ 4923 K 小值查询（分类 + 打标记，Code）