Part2-求AX=b的最优解
自己一边听课一边记得，参考网上广为流传的那本《MIT线性代数笔记》，转成Latex上传太麻烦，直接截图上传了，需要电子版的可以私信我。
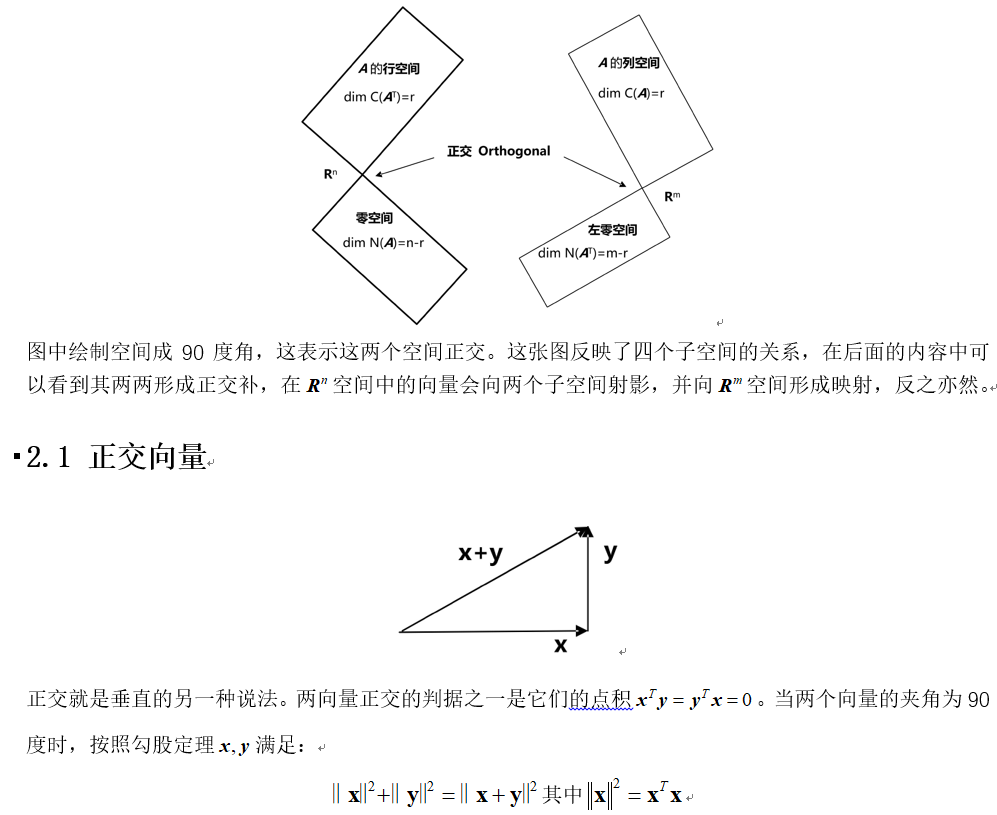
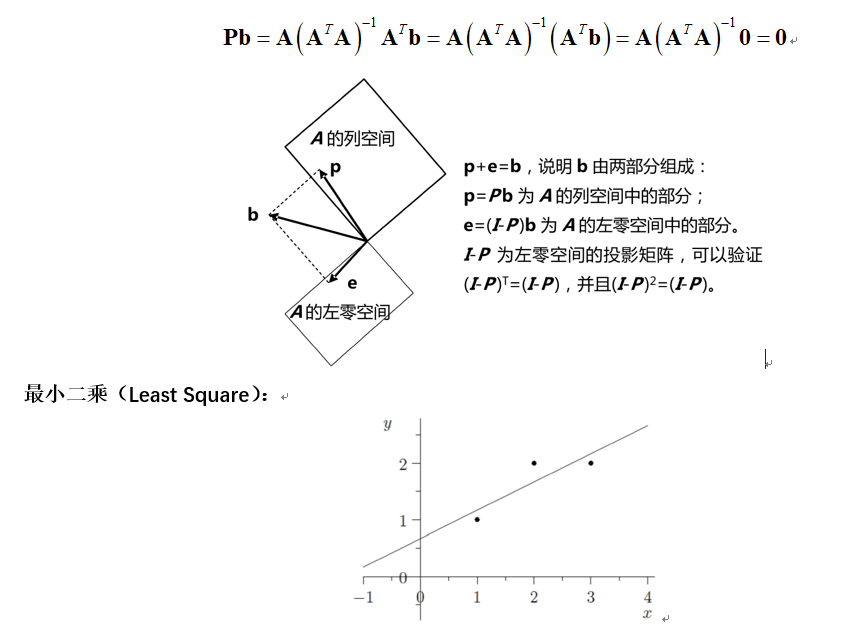
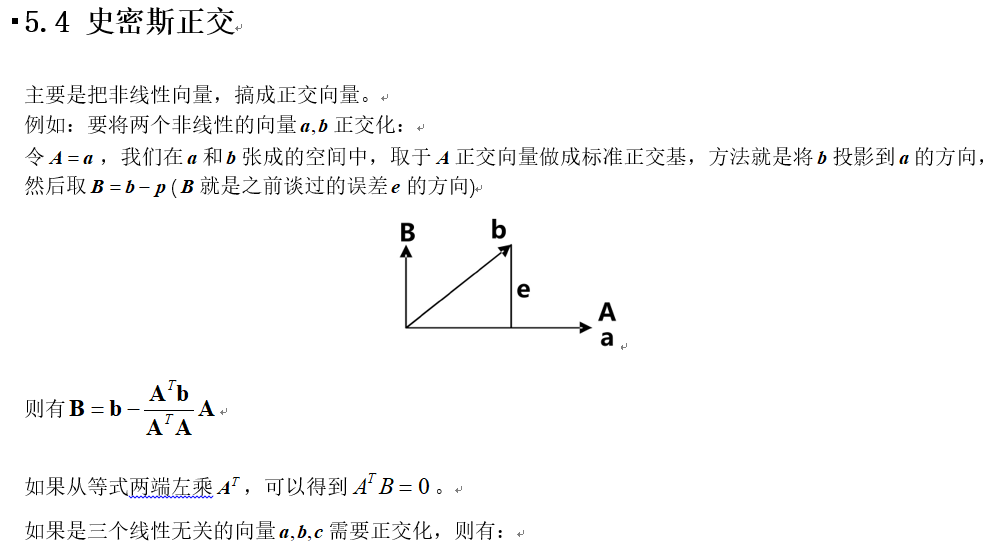
Part2-求AX=b的最优解的更多相关文章
- 扩展欧几里得 求ax+by == n的非负整数解个数
求解形如ax+by == n (a,b已知)的方程的非负整数解个数时,需要用到扩展欧几里得定理,先求出最小的x的值,然后通过处理剩下的区间长度即可得到答案. 放出模板: ll gcd(ll a, ll ...
- 模板——扩展欧几里得算法（求ax+by=gcd的解）
Bryce1010模板 /**** *扩展欧几里得算法 *返回d=gcd(a,b),和对应等式ax+by=d中的x,y */ long long extend_gcd(long long a,long ...
- 拓展欧几里得求 ax + by = c的通解（a >=0, b >= 0）
#include <iostream> #include <cstdio> #include <algorithm> #include <vector> ...
- Matlab求齐次方程的解
% 求Ax=0的解: r=rank(A): x=null(A,r) 求出来x的是归一化后的解.
- 关于ax+by=c的解x，y的min(|x|+|y|)值问题
首先我们移动一下项,并强行让a>b. 然后我们可以画出这样一个图像 我们发现,在线段l与x轴交点处的下方,x,y的绝度值是递增的,所以我们不考虑那个最小点在下端. 之后我们发现在点的上端,因为斜 ...
- C Looooops（扩展欧几里得求模线性方程）
http://poj.org/problem?id=2115 题意:对于C的循环(for i = A; i != B; i+=C)问在k位存储系统内循环多少次结束: 若循环有限次能结束输出次数,否则输 ...
- ZOJ 3593 One Person Game（ExGcd + 最优解）题解
思路:题意转化为求 (ax+by=dis) || (ax+cy=dis) || (bx+cy=dis) 三个式子有解时的最小|x| + |y|.显然求解特解x,y直接用扩展欧几里得,那么怎么求|x| ...
- hdu4686 简单的矩阵快速幂求前n项和
HDU4686 题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4686 题意:题目说的很清楚了,英语不好的猜也该猜懂了,就是求一个表达式的前n项和,矩阵 ...
- 08-求解Ax=b：可解性和解的结构
一.增广矩阵 假设我们要求解方程$Ax=b$,其中矩阵$A$和$b$如下所示: $A = \left[\begin{array}{llll}{1} & {2} & {2} & ...
- 扩展欧几里得(exgcd)-求解不定方程/求逆元
贝祖定理:即如果a.b是整数,那么一定存在整数x.y使得ax+by=gcd(a,b).换句话说,如果ax+by=m有解,那么m一定是gcd(a,b)的若干倍.(可以来判断一个这样的式子有没有解)有一个 ...
随机推荐
- Visual Studio 2019移除/禁用Live Share按钮
Visual Studio 2019新增了几个按钮,搜索按钮,Live Share按钮,发送反馈按钮,管理员按钮(即 “Live Share”, “Send Feedback” ,“ADMIN”) L ...
- nginx负载均衡动态自动更新（微博开源模块nginx-upsync-module使用）
这几天项目有个需求:负载要求能根据节点健康状态动态的增减.nginx自带的upstram已经很强大,而且基于Nginx Upstream配置动态更新已经有很多开源方案,大多数都是基于生成配置文件后进行 ...
- cogs 1176. [郑州101中学] 月考 Map做法
1176. [郑州101中学] 月考 ★★☆ 输入文件:mtest.in 输出文件:mtest.out 简单对比时间限制:1 s 内存限制:128 MB [题目描述] 在上次的月考中B ...
- spark storm 反压
因特殊业务场景,如大促.秒杀活动与突发热点事情等业务流量在短时间内剧增,形成巨大的流量毛刺,数据流入的速度远高于数据处理的速度,对流处理系统构成巨大的负载压力,如果不能正确处理,可能导致集群资源耗尽最 ...
- play framework 相关
1.下载 官网下载解压,安装有jkd即可使用 2.helloworld $ activator new my-first-app play-java https://www.playframework ...
- 曹工说Spring Boot源码（12）-- Spring解析xml文件，到底从中得到了什么（context:component-scan完整解析）
写在前面的话 相关背景及资源: 曹工说Spring Boot源码(1)-- Bean Definition到底是什么,附spring思维导图分享 曹工说Spring Boot源码(2)-- Bean ...
- 使用ajax向后台发送请求跳转页面无效的原因
Ajax只是利用脚本访问对应url获取数据而已,不能做除了获取返回数据以外的其它动作了.所以浏览器端是不会发起重定向的. 1)正常的http url请求,只有浏览器和服务器两个参与者.浏览器端发起一个 ...
- matplotlib 条形图
一.特点 离散数据,数据之间没有直接的关系 二.分类 1.垂直条形图 bar(x, height, width=0.8) # x 为x轴 # height 为y轴 # width 为 条形图的宽度 例 ...
- Codeforces Round #615 (Div. 3) 题解
A - Collecting Coins 题意: 给你四个数a,b,c,d,n.问你是否能将n拆成三个数A,B,C,使得A+a=B+b=C+c. 思路: 先计算三个数的差值的绝对值abs,如果abs大 ...
- tensorboard网络结构
一.tensorboard网络结构 import tensorflow as tffrom tensorflow.examples.tutorials.mnist import input_data ...