【32】Padding（填充）原理讲解

Padding

为了构建深度神经网络，你需要学会使用的一个基本的卷积操作就是padding，让我们来看看它是如何工作的。

 

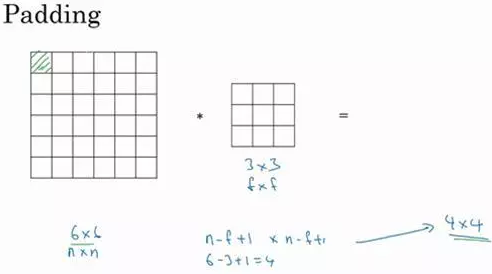
我们在之前笔记中看到，如果你用一个3×3的过滤器卷积一个6×6的图像，你最后会得到一个4×4的输出，也就是一个4×4矩阵。那是因为你的3×3过滤器在6×6矩阵中，只可能有4×4种可能的位置。这背后的数学解释是，如果我们有一个n×n的图像，用f×f的过滤器做卷积，那么输出的维度就是(n-f+1)×(n-f+1)。在这个例子里是6-3+1=4，因此得到了一个4×4的输出。

这样的话会有两个缺点，第一个缺点是每次做卷积操作，你的图像就会缩小，从6×6缩小到4×4，你可能做了几次之后，你的图像就会变得很小了，可能会缩小到只有1×1的大小。你可不想让你的图像在每次识别边缘或其他特征时都缩小，这就是第一个缺点。

 

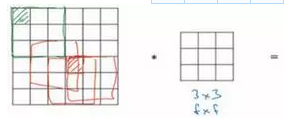
第二个缺点时，如果你注意角落边缘的像素，这个像素点（绿色阴影标记）只被一个输出所触碰或者使用，因为它位于这个3×3的区域的一角。但如果是在中间的像素点，比如这个（红色方框标记），就会有许多3×3的区域与之重叠。所以那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息(第二个缺点)。

为了解决这两个问题，一是输出缩小。当我们建立深度神经网络时，你就会知道你为什么不希望每进行一步操作图像都会缩小。比如当你有100层深层的网络，如果图像每经过一层都缩小的话，经过100层网络后，你就会得到一个很小的图像，所以这是个问题。另一个问题是图像边缘的大部分信息都丢失了。

 

为了解决这些问题，你可以在卷积操作之前填充这幅图像。

在这个案例中，你可以沿着图像边缘再填充一层像素。如果你这样操作了，那么6×6的图像就被你填充成了一个8×8的图像。如果你用3×3的图像对这个8×8的图像卷积，你得到的输出就不是4×4的，而是6×6的图像，你就得到了一个尺寸和原始图像6×6的图像。习惯上，你可以用0去填充，如果p是填充的数量，在这个案例中，p=1，因为我们在周围都填充了一个像素点，输出也就变成了(n+2p-f+1)×(n+2p-f+1)，所以就变成了(6+2×1-3+1)×(6+2×1-3+1)=6×6，和输入的图像一样大。

这个涂绿的像素点（左边矩阵）影响了输出中的这些格子（右边矩阵）。这样一来，丢失信息或者更准确来说角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。

刚才我已经展示过用一个像素点来填充边缘，如果你想的话，也可以填充两个像素点，也就是说在这里填充一层。实际上你还可以填充更多像素。我这里画的这种情况，填充后p=2。

 

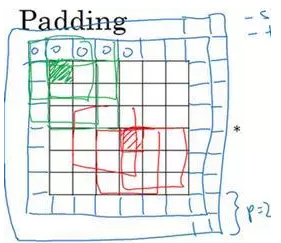
至于选择填充多少像素，通常有两个选择，分别叫做Valid卷积和Same卷积。

Valid卷积

Valid卷积意味着不填充，这样的话，如果你有一个n×n的图像，用一个f×f的过滤器卷积，它将会给你一个(n-f+1)×(n-f+1)维的输出。这类似于我们在前面的笔记频中展示的例子，有一个6×6的图像，通过一个3×3的过滤器，得到一个4×4的输出。

 

Same卷积

另一个经常被用到的填充方法叫做Same卷积，那意味你填充后，你的输出大小和输入大小是一样的。

根据这个公式n-f+1，当你填充p个像素点，n就变成了n+2p，最后公式变为n+2p-f+1。因此如果你有一个n×n的图像，用p个像素填充边缘，输出的大小就是这样的(n+2p-f+1)×(n+2p-f+1)。如果你想让n+2p-f+1=n的话，使得输出和输入大小相等，如果你用这个等式求解p，那么p=(f-1)/2。

所以当f是一个奇数的时候，只要选择相应的填充尺寸，你就能确保得到和输入相同尺寸的输出。这也是为什么前面的例子，当过滤器是3×3时，和上一张幻灯片的例子一样，使得输出尺寸等于输入尺寸，所需要的填充是(3-1)/2，也就是1个像素。另一个例子，当你的过滤器是5×5，如果f=5，然后代入那个式子，你就会发现需要2层填充使得输出和输入一样大，这是过滤器5×5的情况。

 

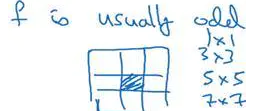
习惯上，计算机视觉中，f通常是奇数，甚至可能都是这样。你很少看到一个偶数的过滤器在计算机视觉里使用，我认为有两个原因。

其中一个可能是，如果f是一个偶数，那么你只能使用一些不对称填充。只有f是奇数的情况下，Same卷积才会有自然的填充，我们可以以同样的数量填充四周，而不是左边填充多一点，右边填充少一点，这样不对称的填充。

第二个原因是当你有一个奇数维过滤器，比如3×3或者5×5的，它就有一个中心点。有时在计算机视觉里，如果有一个中心像素点会更方便，便于指出过滤器的位置。

也许这些都不是为什么f通常是奇数的充分原因，但如果你看了卷积的文献，你经常会看到3×3的过滤器，你也可能会看到一些5×5，7×7的过滤器。后面我们也会谈到1×1的过滤器，以及什么时候它是有意义的。

但是习惯上，推荐你只使用奇数的过滤器。我想如果你使用偶数f也可能会得到不错的表现，如果遵循计算机视觉的惯例，我通常使用奇数值的f。

你已经看到如何使用padding卷积，为了指定卷积操作中的padding，你可以指定p的值。也可以使用Valid卷积，也就是p=0。也可使用Same卷积填充像素，使你的输出和输入大小相同。以上就是padding，在接下来的笔记中我们讨论如何在卷积中设置步长。

作者：极客Array
链接：https://www.jianshu.com/p/4d3ec56e7d05
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。