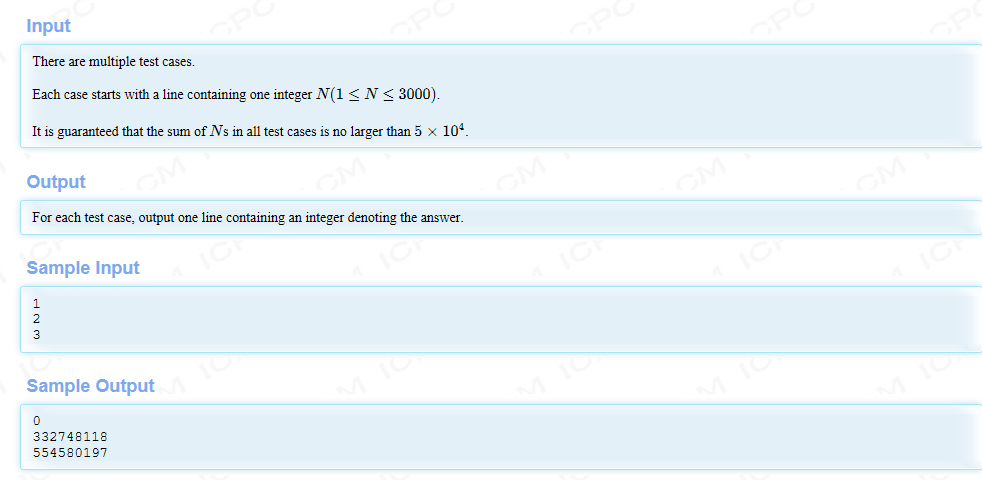
Problem Desciption:

百度翻译后的汉化：

参见博客：https://www.cnblogs.com/zxcoder/p/11253099.html

　　　　　　https://blog.csdn.net/Cassie_zkq/article/details/97255683https://blog.csdn.net/Cassie_zkq/article/details/97255683

ACM的探索之Everything is Generated In Equal Probability! 后序补充丫！的更多相关文章

  1. ACM的探索之Everything Is Generated In Equal Probability(这真的是很有趣的话语丫！)

    ---------------------------------------步履不停,奋勇前进! ------------------------难度真的是蛮大丫!后序补充!

  2. HDU 6595 Everything Is Generated In Equal Probability (期望dp，线性推导)

    Everything Is Generated In Equal Probability \[ Time Limit: 1000 ms\quad Memory Limit: 131072 kB \] ...

  3. 【HDOJ6595】Everything Is Generated In Equal Probability（期望DP）

    题意:给定一个N,随机从[1,N]里产生一个n, 然后随机产生一个n个数的全排列,求出n的逆序数对的数量并累加ans, 然后随机地取出这个全排列中的一个子序列,重复这个过程,直到为空,求ans在模99 ...

  4. hdu多校第二场 1005 （hdu6595） Everything Is Generated In Equal Probability

    题意: 给定一个N,随机从[1,N]里产生一个n,然后随机产生一个n个数的全排列,求出n的逆序数对的数量,加到cnt里,然后随机地取出这个全排列中的一个非连续子序列(注意这个子序列可以是原序列),再求 ...

  5. HDU-多校2-Everything Is Generated In Equal Probability(公式+逆元)

    Problem Description One day, Y_UME got an integer N and an interesting program which is shown below: ...

  6. [hdu6595]Everything Is Generated In Equal Probability

    计算一对逆序对的贡献,即在n个数期望要删多少步才能删掉其中的两个数,设f(n)表示此时的期望,则有方程$f[n]=3/4+(\sum_{i=2}^{n}f[i]\cdot c(n-2,i-2))/2^ ...

  7. ACM学习历程——UVA11234 Expressions（栈，队列，树的遍历，后序遍历，bfs）

    Description   Problem E: Expressions2007/2008 ACM International Collegiate Programming Contest Unive ...

  8. ACM的探索之Keen On Evrything But Triangle（我觉得可以很接近啦！！）

    #include<bits/stdc++.h> using namespace std; int main() { int n,q,l,r; while(cin>>n>& ...

  9. ACM的探索之Just Skip The Problem

    -----------------心怀虔诚,奋勇前进,fighting!!!!!! Problem Description: inclusively:          包括一切地;包含地 simul ...

随机推荐

  1. 与第三方系统对接，生成Cloud出入库单据

    案例: Cloud的采购订单同步到第三方系统,第三方系统入库后同步生成Cloud采购入库单. 解决方案:调用采购订单的下推API,先生成保存状态的采购入库单(采购入库单中的仓库是必填项,可以在采购订单 ...

  2. defender 月考总结

    今天是2019年5月28日,昨天月考了,也是C**生日.昨天考完之后,还是那种考完试的释然感.目前,已经批出来了数学.英语.物理三门学科的成绩,语文还没有批出来.应该明天就能够批出来吧.现在趁着休息, ...

  3. script标签引入脚本的引入位置与效果

    用script标签引入脚本的引入位置大致有两种情况: 1,在head中引入: 2,在body末尾引入: 浏览器由上到下解析代码,正常情况下,先解析head中的代码,在解析body中的代码:放在head ...

  4. 518-零钱兑换 II(完全背包-求方案总数)

    518-零钱兑换 II(完全背包-求方案总数) 给定不同面额的硬币和一个总金额.写出函数来计算可以凑成总金额的硬币组合数.假设每一种面额的硬币有无限个. 示例 1: 输入: amount = 5, c ...

  5. rp算法 随机化 刷题记录

    刷随机化是真的会上瘾quq 洛谷P3973 [TJOI2015]线性代数 看oiwiki上说可以随机化...于是... 就随机在a[i]上选一位取反,然后更新答案,最后输出答案. ...无话可说 代码 ...

  6. [CQOI2009] 中位数 - 桶

    给出 \(1~n\) 的一个排列,统计该排列有多少个长度为奇数的连续子序列的中位数是 \(b\).中位数是指把所有元素从小到大排列后,位于中间的数. Solution (这个题为什么会被打上数学标签? ...

  7. 使用Java代码将一张图片生成为字符画

    测试的图片: 输出的结果: 代码: package test; import java.awt.image.BufferedImage; import java.io.File; import jav ...

  8. MySql 存储大量长字节 Text报错处理办法

    今天线上版本的错误: Caused by: com.mysql.jdbc.exceptions.jdbc4.MySQLSyntaxErrorException: Row size too large ...

  9. android 如何查看socket、websocket通信数据 抓包

    怎么使用可以自行百度

  10. js中的闭包理解

    闭包是一个比较抽象的概念,尤其是对js新手来说.书上的解释实在是比较晦涩,对我来说也是一样. 但是他也是js能力提升中无法绕过的一环,几乎每次面试必问的问题,因为在回答的时候.你的答案的深度,对术语的 ...