https://loj.ac/problem/6620

高中数学好题。。

|kx+b|的函数图像很直观，直接考虑函数图像：

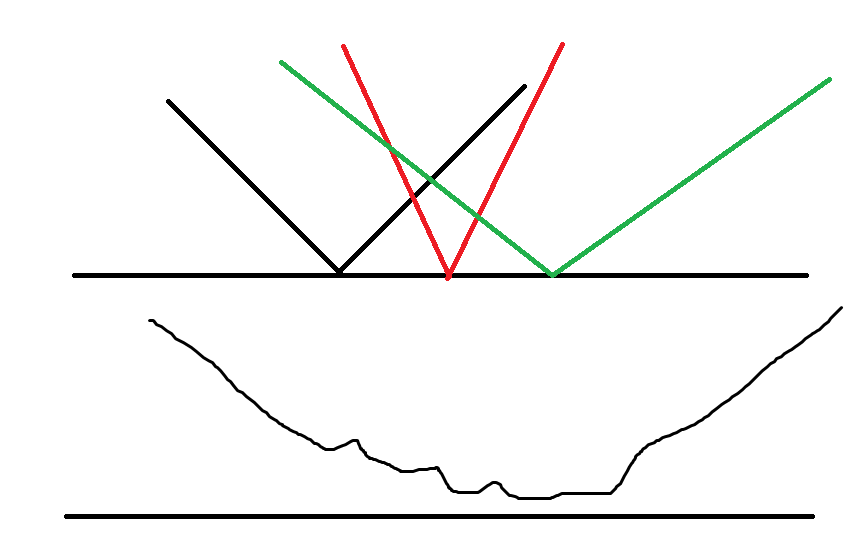
一定只有一段极小值点！

这个点就是最小值了

特点：斜率为0！

而且发现，如果每个|kx+b|的零点作为一个端点的话，那么最小值一定可以在一个端点取到！

（因为两个端点之间是一次函数，最值一定是二者之一）

这个最小值点斜率是负的，下一个就是正的

所以线段树维护斜率和、截距和

加入|kx+b|，分成两段，第一段整体+k,+b第二段同理

二分找到最后一个斜率是负数的点

其实，x的k的值是：

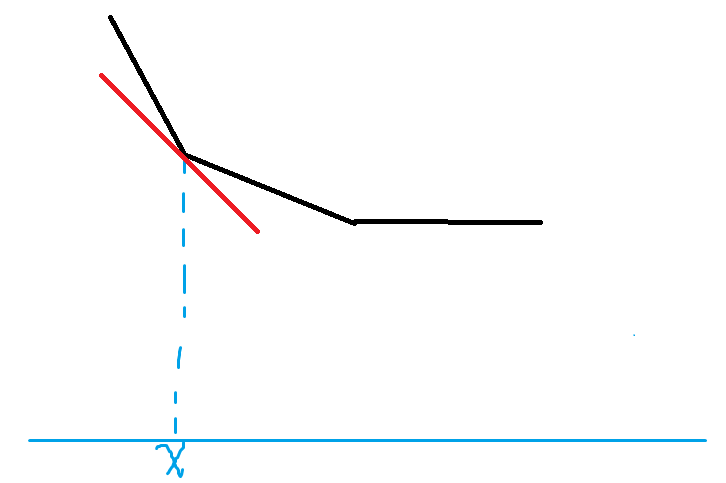
黑色是最后函数图像，

红色的斜率是两个相邻黑边的斜率平均值

「THUPC 2019」不等式 / inequality的更多相关文章

  1. 【LOJ6620】「THUPC 2019」不等式 / inequality（线段树）

    点此看题面 大致题意: 给你两个长度为\(n\)的数组\(a_i\)和\(b_i\),定义\(f_k(x)=\sum_{i=1}^k|a_ix+b_i|\),对于\(k=1\sim n\)的每个\(f ...

  2. 【题解】#6622. 「THUPC 2019」找树 / findtree(Matrix Tree+FWT)

    [题解]#6622. 「THUPC 2019」找树 / findtree(Matrix Tree+FWT) 之前做这道题不理解,有一点走火入魔了,甚至想要一本近世代数来看,然后通过人类智慧思考后发现, ...

  3. 「WC 2019」数树

    「WC 2019」数树 一道涨姿势的EGF好题,官方题解我并没有完全看懂,尝试用指数型生成函数和组合意义的角度推了一波.考场上只得了 44 分也暴露了我在数数的一些基本套路上的不足,后面的 \(\ex ...

  4. LOJ#3054. 「HNOI 2019」鱼

    LOJ#3054. 「HNOI 2019」鱼 https://loj.ac/problem/3054 题意 平面上有n个点,问能组成几个六个点的鱼.(n<=1000) 分析 鱼题,劲啊. 容易想 ...

  5. #3146. 「APIO 2019」路灯

    #3146. 「APIO 2019」路灯 题目描述 一辆自动驾驶的出租车正在 Innopolis 的街道上行驶.该街道上有 \(n + 1\) 个停车站点,它们将街道划分成了 \(n\) 条路段.每一 ...

  6. #3145. 「APIO 2019」桥梁

    #3145. 「APIO 2019」桥梁 题目描述 圣彼得堡市内所有水路长度总和约 282 千米,市内水域面积占城市面积的 7%.--来自维基百科 圣彼得堡位于由 \(m\) 座桥梁连接而成的 \(n ...

  7. #3144. 「APIO 2019」奇怪装置

    #3144. 「APIO 2019」奇怪装置 题目描述 考古学家发现古代文明留下了一种奇怪的装置.该装置包含两个屏幕,分别显示两个整数 \(x\) 和 \(y\). 经过研究,科学家对该装置得出了一个 ...

  8. Solution -「CTS 2019」「洛谷 P5404」氪金手游

    \(\mathcal{Description}\)   Link.   有 \(n\) 张卡牌,第 \(i\) 张的权值 \(w_i\in\{1,2,3\}\),且取值为 \(k\) 的概率正比于 \ ...

  9. 「HNOI 2019」白兔之舞

    一道清真的数论题 LOJ #3058 Luogu P5293 题解 考虑$ n=1$的时候怎么做 设$ s$为转移的方案数 设答案多项式为$\sum\limits_{i=0}^L (sx)^i\bin ...

随机推荐

  1. bnd.bnd属性文件格式

    1.Header以大写字母开头 Bundle-Name: StoreAdminProductsTool 2.Instruction以-和小写字母开头 -sources: true 3. Macro形式 ...

  2. Elasticsearch 启动需要密码？

    vagrant@homestead:~$ systemctl disable elasticsearch.service Synchronizing state of elasticsearch.se ...

  3. 跟我一起认识axure（二）

    创建企业网站页面步骤 第一步修改这里 变成 第一部分就完成了 第二部分部件窗口 在Axure中设计页面像小时候玩的拼图游戏,那么部件窗口就是专门用来存放拼图块的容器 使用部件窗口中常用的部件设计欢迎页 ...

  4. 装了ubuntu之后，只能进入ubuntu系统，不能进入windows系统

    电脑之前安装的是Windows 7系统, 后来在安装Linux系统中(快要完成)出现了故障, 没办法只能关机,之后重启,重启后只能进入Linux系统了 解决方案: 使用sudo update-grub ...

  5. MUI - 封装localStorage与plus.storage

    MUI - 封装localStorage与plus.storage 2.0版本 在使用plus.storage频繁地存取数据时,可以感觉到明显的卡顿,而且很耗内存, 在切换到localstorage时 ...

  6. Add Binary字符数字相加，字符串合成

    Given two binary strings, return their sum (also a binary string). For example,a = "11"b = ...

  7. Selenium-----wait的三种等待

    在UI自动化测试中,必然会遇到环境不稳定,网络慢的情况,这时如果你不做任何处理的话,代码会由于没有找到元素,而报错.这时我们就要用到wait(等待),而在Selenium中,我们可以用到一共三种等待, ...

  8. nodeJs学习-12 consolidate适配各种模板引擎

    const express=require('express'); const static=require('express-static'); const cookieParser=require ...

  9. 数据人看Feed流-架构实践

    背景 Feed流:可以理解为信息流,解决的是信息生产者与信息消费者之间的信息传递问题.我们常见的Feed流场景有:1 手淘,微淘提供给消费者的首页商品信息,用户关注店铺的新消息等2 微信朋友圈,及时获 ...

  10. 关于redis的问题：RedisException with message read error on connection

    最近碰到在REDIS执行一步get操作的时候报出错误:Uncaught RedisException: read error on connection,感觉不可理解,REDIS连接没有发现问题,但是 ...