BZOJ 4034"树上操作"（DFS序+线段树）

传送门

•题意

　　有一棵点数为 N 的树，以点 1 为根，且树点有边权。

　　然后有 M 个操作，分为三种：

　　　　操作 1 ：把某个节点 x 的点权增加 a 。

　　　　操作 2 ：把某个节点 x 为根的子树中所有点的点权都增加 a 。

　　　　操作 3 ：询问某个节点 x 到根的路径中所有点的点权和。

　　输出操作 3 对应的答案；

•题解

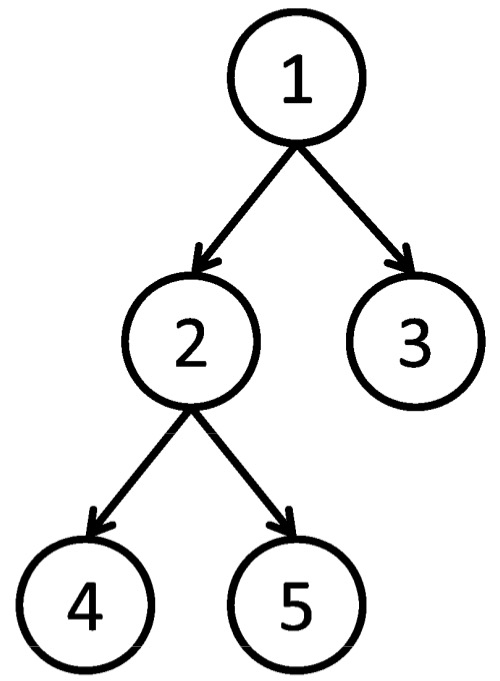
　　如果可以将树形结构转化成链式结构，那么，操作 1，2 就可以用线段树来维护；

　　$1,2,4,4,5,5,2,3,3,1$

　　定义 $s,e$ 分别记录每个节点在序列中第一次出现的位置和最后一次出现的位置；

　　那么，第一次出现的位置权值为正，最后一次出现的位置权值为负；

　　这样的话，就可以通过线段树来维护；

　　操作 1 就对应线段树中的单点更新操作；

　　操作 2 就对应线段树中的区间更新操作；

　　操作 3 就是区间查询操作；

•Code

 #include<bits/stdc++.h>
 using namespace std;
 #define ll long long
 #define ls(x) (x<<1)
 #define rs(x) (x<<1|1)
 #define mem(a,b) memset(a,b,sizeof(a))
 const int maxn=1e5+;

 int n,m;
 int a[maxn];
 int num;
 int head[maxn];
 struct Edge
 {
     int to;
     int next;
 }G[maxn<<];
 void addEdge(int u,int v)
 {
     G[num]={v,head[u]};
     head[u]=num++;
 }
 struct Seg
 {
     int l,r;
     ll lazy;
     ll sum;
     int x;///沿叶子方向的节点个数
     int y;///沿根方向的节点个数
     int mid(){return l+((r-l)>>);}
     void Set(ll val)
     {
         ///如果[l,r]区间的每个节点都增加val
         ///那么，[l,r]区间中沿叶子方向的x个节点增加+val
         ///[l,r]区间中沿根方向的y个节点增加-val
         lazy += val;
         sum += 1ll*(x-y)*val;
     }
 }seg[maxn<<];
 int cnt;
 int s[maxn];
 int e[maxn];
 int vs[maxn<<];
 bool g[maxn<<];

 void DFS(int u,int f)
 {
     vs[++cnt]=u;
     s[u]=cnt;
     g[cnt]=;
     for(int i=head[u];~i;i=G[i].next)
     {
         int v=G[i].to;
         if(v != f)
             DFS(v,u);
     }
     vs[++cnt]=u;
     e[u]=cnt;
     g[cnt]=;
 }
 void pushUp(int pos)
 {
     seg[pos].x=seg[ls(pos)].x+seg[rs(pos)].x;
     seg[pos].y=seg[ls(pos)].y+seg[rs(pos)].y;
     seg[pos].sum=seg[ls(pos)].sum+seg[rs(pos)].sum;
 }
 void pushDown(int pos)
 {
     ll &lazy=seg[pos].lazy;
     if(!lazy)
         return ;

     seg[ls(pos)].Set(lazy);
     seg[rs(pos)].Set(lazy);

     lazy=;
 }
 void build(int l,int r,int pos)
 {
     seg[pos]={l,r,,,,};

     if(l == r)
     {
         if(g[l])
         {
             seg[pos].x++;
             seg[pos].sum=a[vs[l]];
         }
         else
         {
             seg[pos].y++;
             seg[pos].sum=-a[vs[l]];
         }

         return ;
     }

     int mid=seg[pos].mid();
     build(l,mid,ls(pos));
     build(mid+,r,rs(pos));

     pushUp(pos);
 }
 void update(int pos,int l,int r,int x)
 {
     if(seg[pos].l == l && seg[pos].r == r)
     {
         seg[pos].Set(x);
         return ;
     }
     pushDown(pos);

     int mid=seg[pos].mid();
     if(r <= mid)
         update(ls(pos),l,r,x);
     else if(l > mid)
         update(rs(pos),l,r,x);
     else
     {
         update(ls(pos),l,mid,x);
         update(rs(pos),mid+,r,x);
     }
     pushUp(pos);
 }
 ll query(int pos,int l,int r)
 {
     if(seg[pos].l == l && seg[pos].r == r)
         return seg[pos].sum;
     pushDown(pos);

     int mid=seg[pos].mid();
     if(r <= mid)
         return query(ls(pos),l,r);
     else if(l > mid)
         return query(rs(pos),l,r);
     else
         return query(ls(pos),l,mid)+query(rs(pos),mid+,r);
 }
 void Solve()
 {
     cnt=;
     DFS(,);
     build(,cnt,);

     while(m--)
     {
         int op;
         scanf("%d",&op);
         if(op == )
         {
             int u,x;
             scanf("%d%d",&u,&x);
             update(,s[u],s[u],x);
             update(,e[u],e[u],x);
         }
         else if(op == )
         {
             int u,x;
             scanf("%d%d",&u,&x);
             update(,s[u],e[u],x);
         }
         else
         {
             int u;
             scanf("%d",&u);
             printf("%lld\n",query(,s[],s[u]));
         }
     }
 }
 void Init()
 {
     num=;
     mem(head,-);
 }
 int main()
 {
 //    freopen("C:\\Users\\hyacinthLJP\\Desktop\\C++WorkSpace\\in&&out\\contest","r",stdin);
     scanf("%d%d",&n,&m);
     for(int i=;i <= n;++i)
         scanf("%d",a+i);

     Init();
     for(int i=;i < n;++i)
     {
         int u,v;
         scanf("%d%d",&u,&v);
         addEdge(u,v);
         addEdge(v,u);
     }
     Solve();

     return ;
 }

•变形

　　此题操作 3 还可改成求解 $u,v$ 路径间的节点权值和；

　　只需在原来的基础上增加个求解 $LCA$ 的代码即可；