详解C/C++中的的：#pragma pack(push) 、#pragma pack(pop) 和#pragma pack()

前言

我们知道结构体内存对齐字节可以通过#pragma pack(n) 的方式来指定。

但是，有没有想过一个问题，某些时候我想4字节对齐，有些时候我又想1字节或者8字节对齐，那么怎么解决这个问题呢？

此时，#pragma pack(push) 和#pragma pack(pop) 以及#pragma pack()应运而生。

看测试代码：（说明，64位GCC，默认8字节对齐）



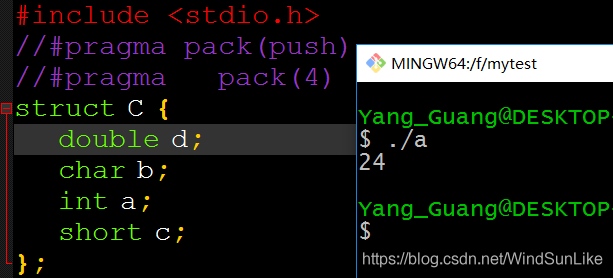
屏蔽了的代码先别看，只看这个结构体，在默认8字节对齐的方式下，sizeof大小为24个字节，这不再做分析，之前随笔分析过了。

pragma pack()

然后我加上强制4字节对齐之后：



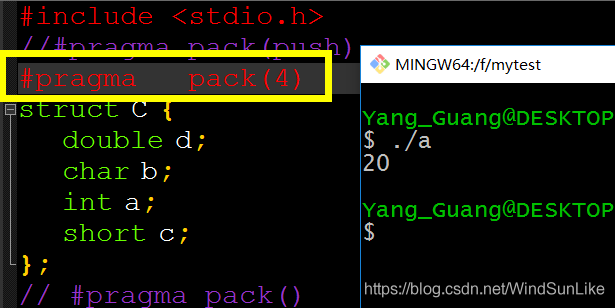
那么现在，我再新建一个结构体B，内容和结构体C一样，只是对齐方式向分别采取不同的方式：

#include <stdio.h>

#pragma   pack(4)
struct C {
    double d;
    char b;
    int a;
    short c;
};
#pragma pack()
struct B {
    double d;
    char b;
    int a;
    short c;
};

像上面那样处理之后，输出：先打印结构C，再打印结构B



这说明了，在强制4字节对齐之后，我加上#pragma pack() ，能够让程序恢复默认对齐（这里是8字节）状态。

#pragma pack() 能够取消自定义的对齐方式，恢复默认对齐。

pragma(pop) & pragma pack(push)

继续测试：

#pragma   pack(4)
struct CC {
    double d;
    char b;
    int a;
    short c;
};
#pragma pack(pop)
struct BB{
    double d;
    char b;
    int a;
    short c;
};

输出：



好像没什么作用的感觉,那么再加上一个#pragma pack(push)试试呢？

#include <stdio.h>

#pragma pack(push)
#pragma   pack(4) 

struct CC {
    double d;
    char b;
    int a;
    short c;
};

#pragma pack(pop) 

struct BB{
    double d;
    char b;
    int a;
    short c;
};
int main(void)
{

    printf("%u\n%u\n",sizeof(struct CC),sizeof(struct BB));
    return 0;
}

这样似乎改变了，有不同的地方体现了出来。

#pragma pack(push)：

英文单词push是“压入”的意思。编译器编译到此处时将保存对齐状态（保存的是push指令之前的对齐状态）。

#pragma pack(pop)：

英文单词pop是”弹出“的意思。编译器编译到此处时将恢复push指令前保存的对齐状态（请在使用该预处理命令之前使用#pragma pack(push)）。

push和pop是一对应该同时出现的名词，只有pop没有push不起作用，只有push没有pop可以保持之前对齐状态（但是这样就没有使用push的必要了）。

这样就可以知道，当我们想要一个结构体按照4字节对齐时，可以使用#pragma pack(4) ，最后又想使用默认对齐方式时，可以使用#pragma pack() ；

也可以使用：

#pragma pack(push)
#pragma pack(4)
struct...
#pragma pack(pop)

这样在push和pop之间的结构体就可以按照pack指定的字节（这里是4字节对齐方式），而pop之后的结构体按照#pragma pack(push) 前对齐方式。

eg：

#include <stdio.h>
#pragma   pack(2)
#pragma pack(push)
#pragma   pack(4)
struct CC {
    double d;
    char b;
    int a;
    short c;
};

#pragma   pack(1)
struct BB{
    double d;
    char b;
    int a;
    short c;
};
#pragma pack(pop)
struct AA{
    double d;
    char b;
    int a;
    short c;
};
int main(void)
{

    printf("%u\n%u\n%u\n",sizeof(struct CC),sizeof(struct BB),sizeof(struct AA));
    return 0;
}

先按照2字节对齐，然后push保存2字节对齐，然后又强制4字节对齐，打印CC为20字节，然后强制1字节对齐，打印BB为15字节，然后pop，pop会让编译器回到push之前的对齐方式（这里是2字节对齐），打印AA（按照2字节对齐）16字节。

注意，#pragma pack() 取消自定义对齐方式，恢复默认方式，而push之后pop是回到push指令之前的对齐方式。

eg：

#include <stdio.h>
#pragma   pack(2)
#pragma pack(push)
#pragma   pack(4)
struct CC {
    double d;
    char b;
    int a;
    short c;
};

#pragma   pack(1)
struct BB{
    double d;
    char b;
    int a;
    short c;
};
#pragma pack()
struct AA{
    double d;
    char b;
    int a;
    short c;
};
int main(void)
{

    printf("%u\n%u\n%u\n",sizeof(struct CC),sizeof(struct BB),sizeof(struct AA));
    return 0;
}

只把pop改成pack()打印如下：



最后回到的不是2字节对齐，而是默认的8字节对齐。

延伸

还有延伸点：



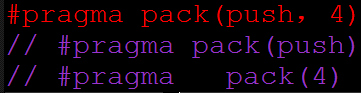
上图红色处等价于它下面的两句。

语法：

#pragma pack( [show] | [push | pop] [, identifier], n )

说明：

1，pack提供数据声明级别的控制，对定义不起作用；

2，调用pack时不指定参数，n将被设成默认值；

3，一旦改变数据类型的alignment，直接效果就是占用memory的减少，但是performance会下降；

语法具体分析：

1，show：可选参数；显示当前packing aligment的字节数，以warning message的形式被显示；

2，push：可选参数；将当前指定的packing alignment数值进行压栈操作，这里的栈是the internal compiler stack，同时设置当前的packing alignment为n；如果n没有指定，则将当前的packing alignment数值压栈；

3，pop：可选参数；从internal compiler stack中删除最顶端的record；如果没有指定n，则当前栈顶record即为新的packing alignment数值；如果指定了n，则n将成为新的packing aligment数值；如果指定了identifier，则internal compiler stack中的record都将被pop直到identifier被找到，然后pop出identitier，同时设置packing alignment数值为当前栈顶的record；如果指定的identifier并不存在于internal compiler stack，则pop操作被忽略；

4，identifier：可选参数；当同push一起使用时，赋予当前被压入栈中的record一个名称；当同pop一起使用时，从internal compiler stack中pop出所有的record直到identifier被pop出，如果identifier没有被找到，则忽略pop操作；

5，n：可选参数；指定packing的数值，以字节为单位；

另外：

__attribute(aligned(n))，让所作用的数据成员对齐在n字节的自然边界上；如果结构中有成员的长度大于n，则按照最大成员的长度来对齐；

__attribute((packed))，取消结构在编译过程中的优化对齐，按照实际占用字节数进行对齐

参考

参考原文：https://www.cnblogs.com/yangguang-it/p/7392726.html