leetcode 1301. 最大得分的路径数目

地址 https://leetcode-cn.com/problems/number-of-paths-with-max-score/

给你一个正方形字符数组 board ，你从数组最右下方的字符 'S' 出发。

你的目标是到达数组最左上角的字符 'E' ，数组剩余的部分为数字字符 1, 2, ..., 9 或者障碍 'X'。在每一步移动中，你可以向上、向左或者左上方移动，可以移动的前提是到达的格子没有障碍。

一条路径的 「得分」 定义为：路径上所有数字的和。

请你返回一个列表，包含两个整数：第一个整数是 「得分」 的最大值，第二个整数是得到最大得分的方案数，请把结果对 10^9 + 7 取余。

如果没有任何路径可以到达终点，请返回 [0, 0] 。

示例 ：

输入：board = ["E23","2X2","12S"]
输出：[,]
示例 ：

输入：board = ["E12","1X1","21S"]
输出：[,]
示例 ：

输入：board = ["E11","XXX","11S"]
输出：[,]
 

提示：

 <= board.length == board[i].length <= 

解答

使用动态规划  因为走到当前的格子肯定是当前格子的右方 下方和右下方。 那么他的右下方 右方和下方的状态中 那些是得分最高的就决定了当前的得分和走法方案数

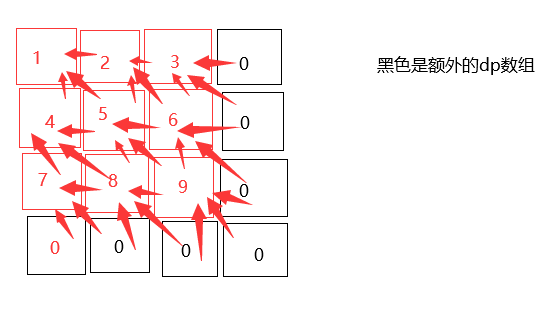
代码如下 注意DP有额外多开一层 为了保持代码的一致性。

代码起点dp判断如下: n = board.size() ;  dp[n-1][n-1] =  max(max(dp[n][n-1], dp[n-1][n]), dp[n][n]);

由于dp初始均为0  所以不影响起点 dp[n-1][n-1]的取值

class Solution {
public:
    vector<vector<int>> dp;
    vector<vector<int>> path;

    vector<int> pathsWithMaxScore(vector<string>& board) {
    const int n = board.size();
    const int MOD = 1e9+;
    dp.resize(n+, vector<int>(n+));
    path.resize(n+,vector<int>(n+));

    board[n - ][n - ] = '';
    board[][] = '';

    path[n - ][n - ] = ;

    for (int i = n - ; i >= ; i--) {
        for (int j = n - ; j >= ; j--) {
            if (board[i][j] == 'X') continue;
            int m  = max(max(dp[i + ][j], dp[i][j + ]), dp[i + ][j + ]);
            dp[i][j] = ( (board[i][j] - '') + m ) %MOD;

            if (dp[i + ][j] == m) path[i][j] = ( path[i][j]+path[i+][j])%MOD;
            if (dp[i + ][j+] == m) path[i][j] = (path[i][j] + path[i + ][j+]) %MOD ;
            if (dp[i][j+] == m) path[i][j] = ( path[i][j]+ path[i][j+])%MOD;
        }
    }
    if(path[][] == ) return vector<int>({,});
    return vector<int>({dp[][],path[][]});
}

};