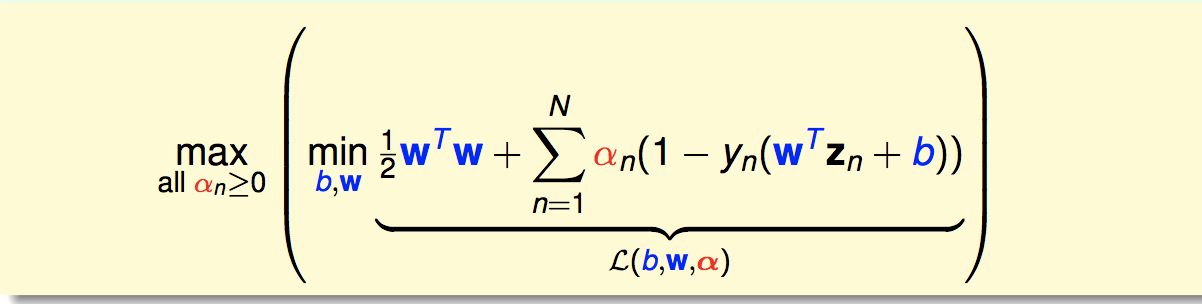对偶SVM
1.对偶问题的推导
为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数。
1.1 用拉格朗日函数将原问题转化为“无约束”等价问题
原问题是:

写出它的拉格朗日函数:

然后我们的原问题就等价为:

为什么可以这样等价:

即:对于不满足约束条件的(b,w),min里面趋于无穷大,因此min就把这些b,w舍去了;对于满足约束条件的解,min里面就刚好是原来的目标函数,刚好与原问题等价。
1.2 导出拉格朗日对偶问题
首先我们有如下成立:

然后我们取右边式子中的“best”阿尔法,仍然会有大于等于号成立,因为best is one of any:

这时右边的式子就是对偶问题。这里直接给出一个定理,当满足下面条件时(对于SVM来说刚好满足),原始问题和对偶问题的解是相同的:

并且它们的最优解满足KKT条件:
1.3 用KKT条件来简化对偶问题
我们的对偶问题现在是:
根据KKT条件,我们有:

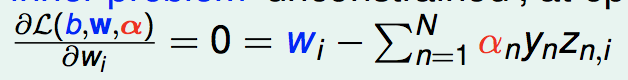
把第一个代进来:

再把第二个代进来:

这时候,我们的问题里面就只剩一个参数阿尔法了。再把平方项展开,写的好看一点,就得到了标准的硬间隔SVM对偶问题:

2. 解对偶问题
还是解QP那一套:

之后再求W和b:
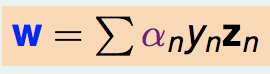 (所有支持向量的加权和)
(所有支持向量的加权和)
 (任取一个支持向量算出)
(任取一个支持向量算出)
3. 支持向量
引出对偶问题后,我们重现定义支持向量为阿尔法大于0的向量。他们一定是在边界上的,但是在边界上的不一定阿尔法大于0:

前面我们也提到过,w和b的计算只需要支持向量,其他向量都是无用的:

对偶SVM的更多相关文章
- 《机器学习技法》---对偶SVM
1.对偶问题的推导 为什么要求解对偶问题?一是对偶问题往往更容易求解,二是可以自然的引入核函数. 1.1 用拉格朗日函数将原问题转化为“无约束”等价问题 原问题是: 写出它的拉格朗日函数: 然后我们的 ...
- SVM原理与实践
SVM迅速发展和完善,在解决小样本.非线性及高维模式识别问题中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中.从此迅速的发展起来,已经在许多领域(生物信息学,文本和手写识别等)都取 ...
- SVM1 线性SVM
一.Linear Support Vector Machine 接下来的讨论假设数据都是线性可分的. 1.1 SVM的引入:增大对测量误差的容忍度 假设有训练数据和分类曲线如下图所示: 很明显,三个分 ...
- SVM学习笔记
一.SVM概述 支持向量机(support vector machine)是一系列的监督学习算法,能用于分类.回归分析.原本的SVM是个二分类算法,通过引入“OVO”或者“OVR”可以扩展到多分类问题 ...
- SVM对偶形式
dual svm 对偶SVM linear SVM 可以用二次规划方法解 xn通过非线性转换变成zn SVM配合非线性特征转换 透过large-margin降低模型复杂度 透过特征转换得到弯弯曲曲的边 ...
- SVM笔记
1.前言 SVM(Support Vector Machine)是一种寻求最大分类间隔的机器学习方法,广泛应用于各个领域,许多人把SVM当做首选方法,它也被称之为最优分类器,这是为什么呢?这篇文章将系 ...
- 【机器学习算法基础+实战系列】SVM
概述 支持向量机是一种二分类模型,间隔最大使它有别于感知机.支持向量机学习方法由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly s ...
- SVM小白教程(2):拉格朗日对偶
在上一篇文章中,我们推导出了 SVM 的目标函数: \[ \underset{(\mathbf{w},b)}{\operatorname{min}} ||\mathbf{w}|| \\ \operat ...
- SVM系列之拉格朗日对偶
在学习SVM(Support Vector Machine) 支持向量机时,对于线性可分的分类样本求出的分类函数为: 其中,分类超平面可以表示为:
随机推荐
- HttpURLConnection类
导语 java.net.HttpURLConnectin类是URLConnection类的抽象子类.它在处理协议为HTTP的URL时特别有效.具体而言,它通过它可以获取和设置请求方法,确定是否重定向, ...
- 【WPF】WPF 布局
1.window 类继承自 ContentControl 所以内部只能有一个元素2.遵循原则: 不应显示的设置元素(控件)尺寸,可以通过设置最大最小尺寸来限制大小 ...
- 表单验证插件之jquery.validate.js
提到表单验证的插件,第一个想到的就是jquery.validate.js,所以小生想在这里稍微详细地说一下这款插件的具体使用方法,便于理解,我直接附上整段demo的代码(没怎么调样式,主要是看js): ...
- Ceph RGW服务 使用s3 java sdk 分片文件上传API 报‘SignatureDoesNotMatch’ 异常的定位及规避方案
import java.io.File; import com.amazonaws.AmazonClientException; import com.amazonaws.auth.profile ...
- PL/SQL异常获取
1.no_data SET SERVEROUTPUT ON DECLARE pename EMP.ENAME % TYPE ; BEGIN SELECT ename INTO pename FROM ...
- php class
一个类可以包含有属于自己的常量,变量(称为"属性")以及函数(称为"方法"). $ 变量--专业术语上称它为"属性". function ...
- Unity Animator动画状态机 深入理解(一)
接触Unity以来就已经有了Animator,Animation用的少,不过也大概理解他俩之间的一个区别于联系. 图中其实就是Animator和Animation之间的区别于联系了,啊!你肯定会告诉我 ...
- struts-validate.xml配置详解demo
<?xml version="1.0" encoding="UTF-8"?> <!DOCTYPE validators PUBLIC &quo ...
- mysql 查询制定日期数据
//获取昨天更新数据的条件date_sub(current_date(), interval 1 day) = from_unixtime(senddate, '%Y-%m-%d') 注释:date_ ...
- easyui datagrid 悬浮事件
easyui的单元格提示窗体 鼠标悬浮事件 function findAllPreven() { var infoname = $('#area').val(); areadatagrid=$('# ...