『实践』Yalmip+Ipopt+Cplex使用手册

Yalmip+Ipopt+Cplex使用手册

1.软件版本

• Cplex 12.6.2，Matlab R2014a，Ipopt 3.12.9，Yalmip

2.Cplex添加方法

• 官方下载地址: http://www-01.ibm.com/software/websphere/products/optimization/cplex-studio-community-edition/

• 破解版下载地址：http://www.0daydown.com/02/140054.html

• 其中community-edition可以免费试用，但最多只能计算1000个变量或1000个约束条件的优化问题。

• 点击安装，安装步骤默认操作即可。

• 点击Matlab中的，点击，找到路径并将其添加，最后点击即可。

• 然后在Matlab命令行窗口输入，出现帮助文档，代表添加成功。

3.Ipopt添加方法

• 需要的组件：VC_redist.x64和ww_ifort_redist_intel64_2017.0.109.msi

• (组件下载地址链接：链接1：https://pan.baidu.com/s/1f-J5PBu1WsJO8uxyZzbcTQ 密码：crxv )

• 链接2：

• 在打开的界面中选择图1-1即可。

图1

• Ipopt下载地址：https://www.inverseproblem.co.nz/OPTI/index.php/DL/DownloadOPTI（最新版本3.12.9）
• Ipopt下载链接：链接：https://pan.baidu.com/s/1tWBRJ7syW-WctcL1LkB06w 密码：1n3m （以前的版本3.12.6）
• 下载下来后解压缩，打开文件，目录如下图1-2。

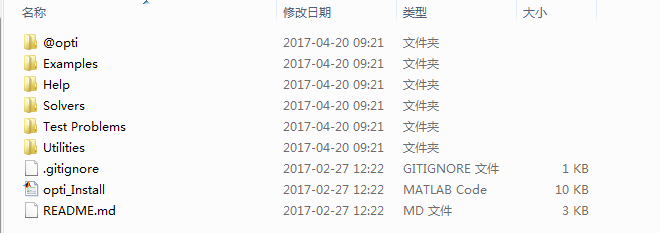
图2

• 打开MATLAB，设置路径-》添加并包含子文件夹-》选择Ipopt路径-》保存。见下图1-3。

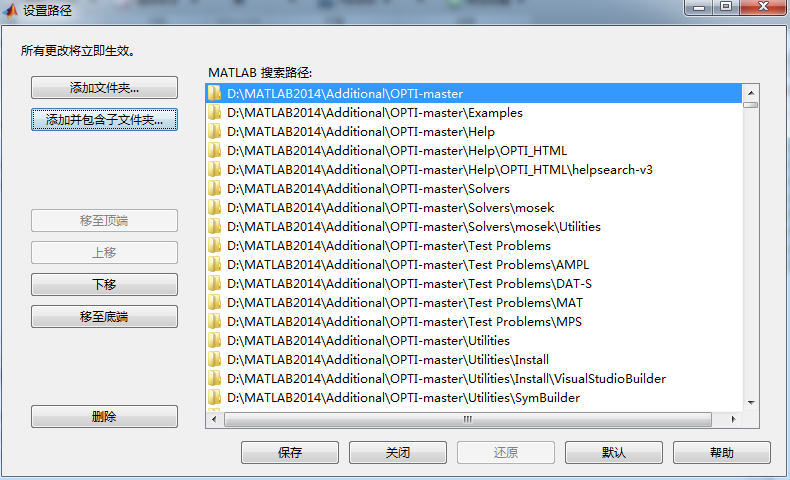
图3

• 右键运行图2中的opti_Install。
• 出现提示让你安装optiMEXFiles_mexw64_2_27，回车几下，弹出窗口，找到optiMEXFiles_mexw64_2_27（不需要自己手动解压）选中即可。
• VC_redist.x64和ww_ifort_redist_intel64_2017.0.109.msi ，这两个组件自己手动安装，注意版本即可。
• 注意下图中框框中的组件我已经安装好了，如果没有安装，是会有提示的。
• 

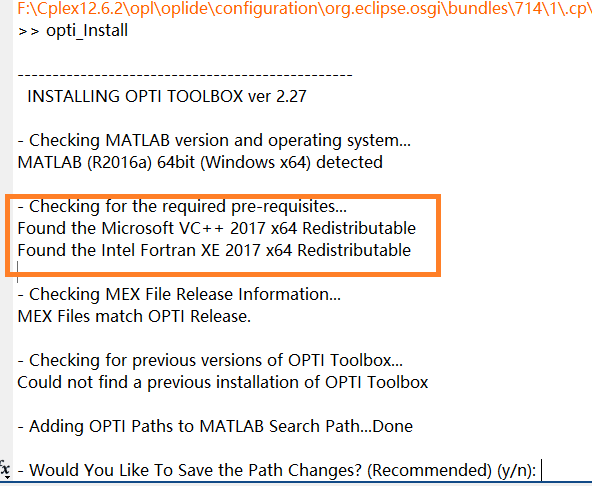
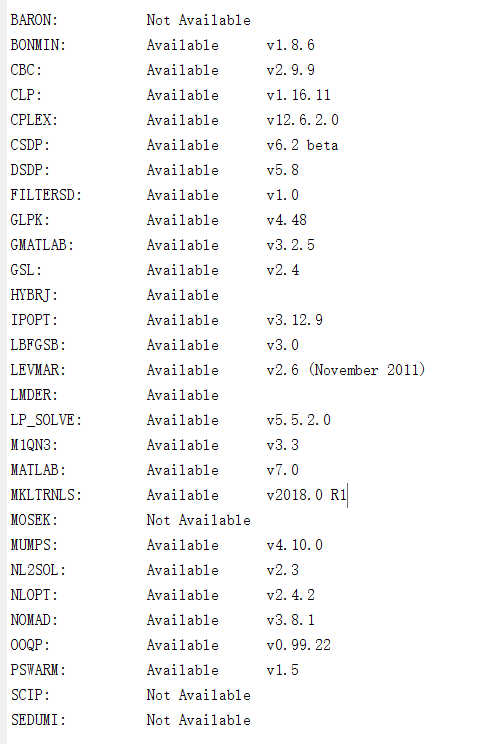
IPOPT 3.12.9

4.Yalmip添加方法

• 下载地址：https://yalmip.github.io/（最新版本）
• 下载链接：http://pan.baidu.com/s/1eRBhRlK 密码：dv4o（之前版本）
• 将下载的文件解压，设置路径-》添加并包含子文件夹-》选择Yalmip路径-》保存。
• 在Matlab的命令行窗口中输入或输入Yalmiptest，测试是否添加成功。

5.Yalmip建模常用语法

5.1  变量设置

• 实数变量：sdpvar；
• 0-1变量：binvar；
• 整数变量：intvar。
• 例如:x = sdpvar(1,1);    %x为1×1的实数变量

5.2  约束条件

• Constraints = [];　　%Constraints为自己定义的一个存储约束的矩阵
• Constraints = [Constraints,0 <= x  <= 1];   %定义了一个变量x大于0且小于1的约束条件

5.3  目标函数

• F = 0;    %F为目标函数
• x = sdpvar(1,1);
• Constraints = [Constraints, x >= 2];
• F = F + x^2 + x^3;   %目标函数为x^2+x^3

5.4   查看变量或表达式的值

• value(x);   %查看变量x的值
• value(x^2+x^3);   %查看表达式x^2+x^3的值

5.5  设置Yalmip和求解器的options

• 通过sdpsettings设置，(sdpsettings参数列表链接）
• options = sdpsettings('field',value,'field',value,.....);   %filed为参数名，value为设置值
• 例如：options = sdpsettings('solver','cplex');   %设置求解器为cplex
• 或者这样也可以：options.cplex.exportmodel = 'model.lp';   %设置求解器cplex输出lp格式的数学模型，文件名为model。

图4

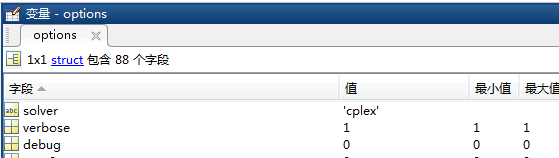
图5   options

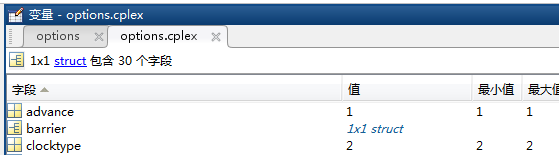
图6  options.cplex

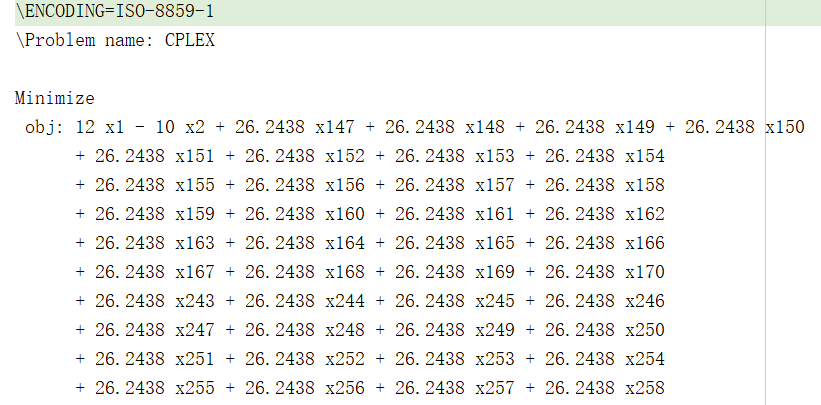
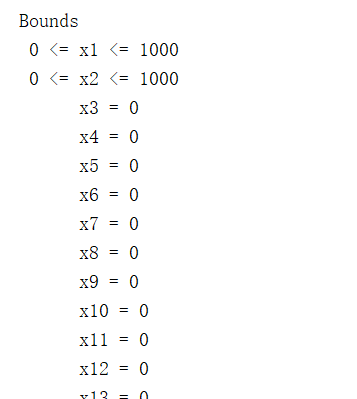
图7     xxxx.lp格式的数学模型

5.6  常用求解函数optimize

• sol = optimize(Constraints,Objective,options);  %Constraints为约束，Objective为目标函数，options为5.5节的options

5.7 输出Yalmip模型

• export函数是将Yalmip模型按照求解器的格式输出。
• [model,recoverymodel,diagnostic,internalmodel] = export(Constraints,Objective,options);  %Constraints为约束，Objective为目标函数，options为5.5节的options
• 例如：
• x = intvar(2,2);
• Constraints = [];
• Constraints = [Constraints,0 <= x  <= 1];
• F = sum(x) * ones(2,1);
• options = sdpsettings('solver','cplex');   %设置求解器为cplex
• [model,recoverymodel,diagnostic,internalmodel] = export(Constraints,Objective,options);  %此时model中就会有符合cplex求解器格式的模型

图8  model中的参数列表

5.8  获取求解器的求解时间和Yalmip的建模时间

• sol = optimize(Constraints,Objective,options);  %Constraints为约束，Objective为目标函数，options为5.5节的options
• sol.yalmiptime;  %Yalmip的建模时间
• sol.solvertime;  %求解器的求解时间

5.9  设置初值

• P = sdpvar(2,2);
• assign(P,double(Pit));  %P为2×2的实数变量，Pit为2×2的已知矩阵，将Pit的值赋值给P
• options = sdpsettings('solver','cplex','usex0',1);  %usex0默认为0，1为开启设置初值功能

图9   Yalmip网站说明

5.10  获取对偶乘子

• 查看我的另一篇博客：『实践』Yalmip获取对偶函数乘子

5.11  Yalmip输出模型，调用Cplex类求解

• 查看我的另一篇博客:：『实践』Yalmip建模+Cplex类求解

5.12  IPOPT参数设置说明

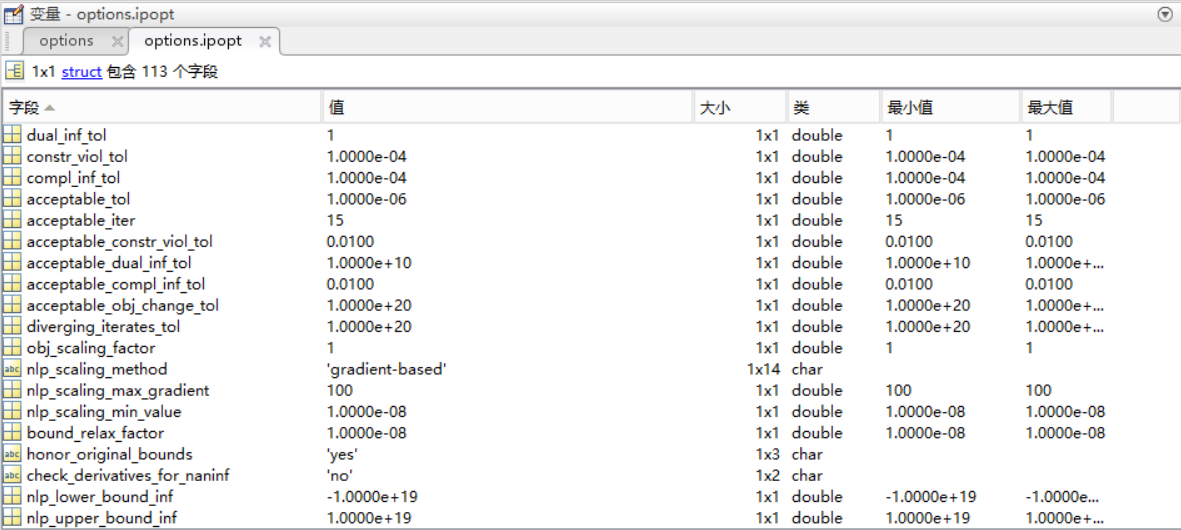
图10 IPOPT参数列表

• IPOPT中参数的说明详见：  https://www.gams.com/latest/docs/S_IPOPT.html#IPOPTpardiso_max_iterative_refinement_steps